基于事件触发的拓扑切换异构多智能体协同输出调节

杨若涵 张皓 严怀成

基于事件触发的拓扑切换异构多智能体协同输出调节

杨若涵1张皓1严怀成2,3

研究切换拓扑下线性异构多智能体系统的协同输出调节问题,并设计了一个基于事件触发的输出调节控制机制.设计的控制机制不仅可以实现智能体对外部系统的渐近跟踪和干扰抑制,还可以有效减少智能体之间的信息传递数量,从而降低通信负载减少网络能耗.最后通过仿真验证结论的有效性.

异构多智能体系统,协同输出调节,事件触发控制,切换拓扑

协同输出调节[1]的目标是设计一种控制器从而使多智能体系统实现对外部系统信号的渐近跟踪和干扰抑制.由于多智能体系统的一致性[2−7]和编队问题[8−10]等都能作为协同输出调节问题的一种特殊情况,协同输出调节引起了学者的广泛关注.Wang等[11]设计了一种基于分布式内膜法的控制器用来解决异构多智能体系统的协同输出调节问题,同时假设系统的通信拓扑图中没有自环.Su等[12]提出了一种基于分布式观测器的输出调节控制器.在设计控制器时,将子系统分为两部分:一部分可以直接得到外部系统的信号;一部分不能直接得到外部系统的信号.Tang等[13]研究了非线性系统的输出调节问题,提出的分布式控制器使跟随者能够在领导者含有未知输入的情况下实现对领导者状态的跟踪.

上述文章都考虑智能体之间信号连续传输的情况,然而信号连续传输会引起较大的网络通信负载和通信能量浪费.为了解决这一问题,提出了事件触发传输机制.在事件触发传输机制中,只有当系统的实际状态和参考水平之间的差距大于一定阈值,即系统发生较大变化时,才对当前时刻状态进行更新.因此,事件触发传输机制能够有效降低系统通信次数,减少通信资源的使用[14−15].

Wang等[16]研究了基于内膜控制的事件触发协同输出调节问题.文章假设多智能体是同构的,这种假设具有一定的局限性.Hu等[17]研究了基于分布式观测器的事件触发多智能体协同输出问题.然而在设计事件触发条件时,智能体需要连续知道相邻节点状态;在设计控制器时,当智能体触发,其邻居节点需要发送当前时刻的状态值.

本文首先设计了一种基于事件触发的观测器用来观测外部系统的信号.这个观测策略可以有效减少各个节点之间的通信次数,从而降低网络通信负载和通信能耗.然后在设计的事件触发观测器的基础上,提出了一种基于输出反馈的输出调节控制策略,在此策略的作用下,异构多智能体能够实现对外部系统信号的渐近跟踪和干扰抑制.

符号说明:Rn×n表示n×n维的实矩阵集合.AT表示A的转置.A⊗B表示矩阵A和B的Kronecker乘积.‖A‖表示矩阵A的范数.diag{A1,···,AN}表示对角线上的项为Ai,i=1,···,N的区块对角矩阵.

1 图论及问题描述

1.1 图论

有向图可以用G={V,E}表示,其中V∈{0,···,N}表示节点,E∈V×V表示边.若节点i和节点j相邻,则用 (i,j)表示从节点 i到节点 j的边.若在图 G中,任意i,j∈V可以推出 (i,j)∈E⇔(j,i)∈E,则图G为无向图. Ni表示节点i的邻居节点.如果在图中至少有一个节点存在通向其他所有节点的有向路径,则称这个图包含一个有向生成树.节点0表示外部系统,节点1,···,N表示N个智能体,因此由多智能体系统和外部系统共同构成的通信拓扑的拉氏矩阵可以表示为L=[lij]∈R(N+1)×(N+1).当i=j时,lii=∑j∈Niaij;当 i/=j时,lij=−aij.若节点i与节点j之间存在通信,则aij＞0;反之,aij=0.当图G包含有向生成树时,拉氏矩阵可以表示为

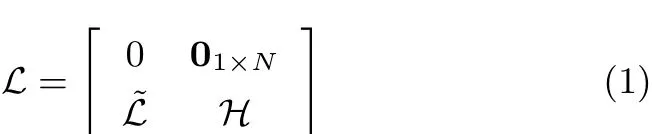
其中,H∈RN×N为非奇异M 矩阵,且满足L1N+1=0, 1N+1=[1,···,1]T是一个N+1维的向量.

定义 1.对于方阵 A=[aij]∈RN×N,若 aii＞0, aij≤0,i/=j,且矩阵A的逆矩阵为非负矩阵,则矩阵A被称为非奇异M 矩阵.若矩阵A为非奇异M 矩阵，则矩阵A的所有特征值的实部皆为正.

1.2 问题描述

考虑异构多智能体系统

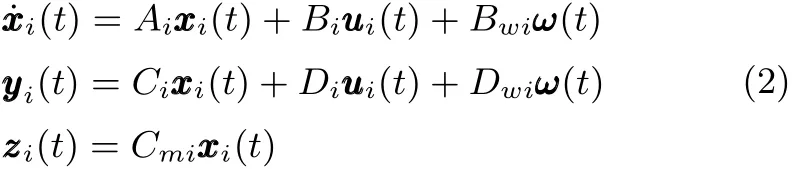
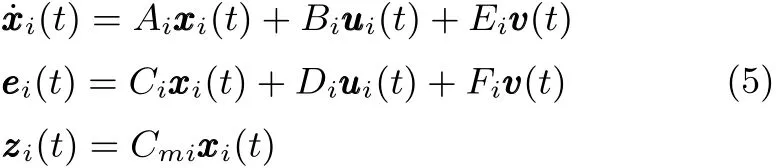
其中Ei=[Bwi0],Fi=[Dwi−I].

在本文中,切换拓扑由 Gσ(t)表示,其中 σ(t) : [0,+∞)→ {1,···,s}为通信拓扑的切换信号.在对主要结论进行推导前,首先给出如下假设和定义.

假设1.矩阵Av的所有特征值的实部均非负.

假设2.(Ai,Bi)可控.

假设3.(Ai,Ci)可观.

假设4.所有通信拓扑都是有向图且包含有向生成树.

定义2.对于多智能体系统(5),假设通信拓扑Gσ(t)是有向的且具有一个生成树.设计控制器,满足

2 事件触发控制机制的设计

在对输出调节控制器进行设计之前,首先要对外部信号v(t)进行观测,观测器设计如下

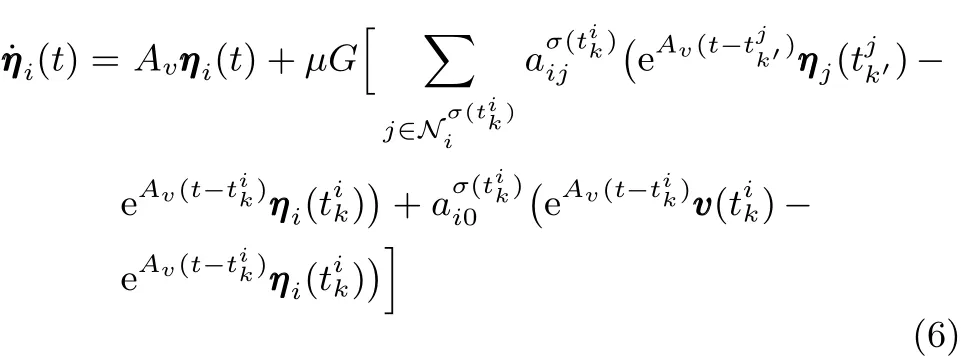
注1.在一般的通信拓扑切换系统中,观测器根据当前时刻通信拓扑Gσ(t)的变化进行更新.然而在事件触发传输策略下,智能体只在触发时刻广播其状态信息,在触发间隔内不进行信息交互.因此,在区间内,只有触发时刻的通信拓扑Gσ(tik)影响观测器更新.

定义当前时刻与上一触发时刻之间的状态测量误差为

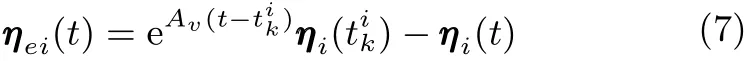
注 2.在一阶多智能体系统中,当智能体状态实现对外部信号的跟踪时,和状态测量误差

将收敛至零.然而,在一般多智能体系统中,若设计与一阶系统相同的和和无法同时趋近于零.

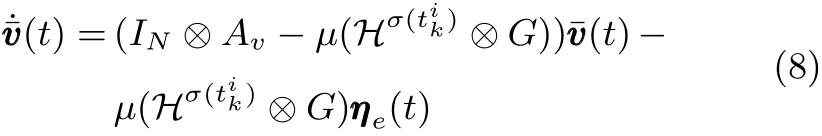
定理1.如果假设1和4满足,给定常数γ＞0,0＜δ＜1,α＞0,P满足Riccati方程PAv+ATvP−γPP+αI=0.事件触发条件为设计观测器 (6), 其中参数观测器增益 G=P.则观测器(6)能够实现对外部信号的渐近跟踪,且跟踪误差渐近衰减至零.

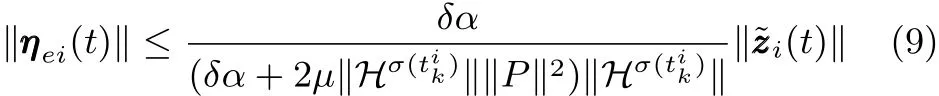
证明.选择Lyapunov-Krasovskii方程

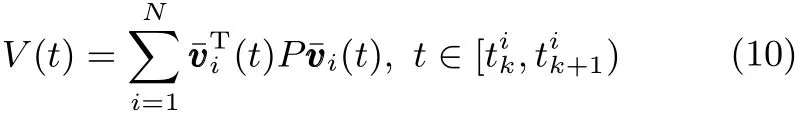
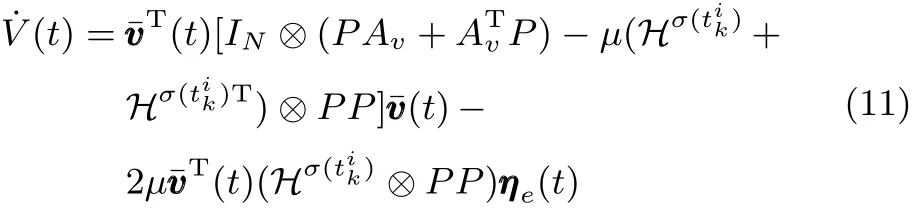
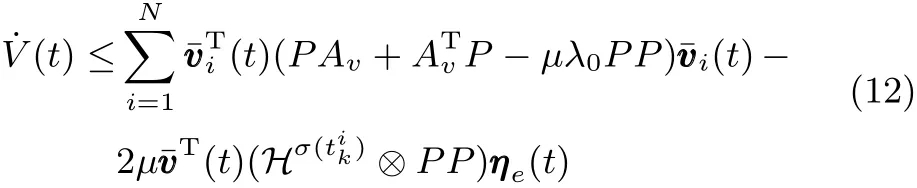
令 µλ0≥ γ,给定 α ＞ 0,存在正定矩阵 P 满足从式(12)可以得到

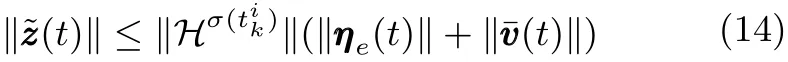
即

将式(15)代入式(13),则有

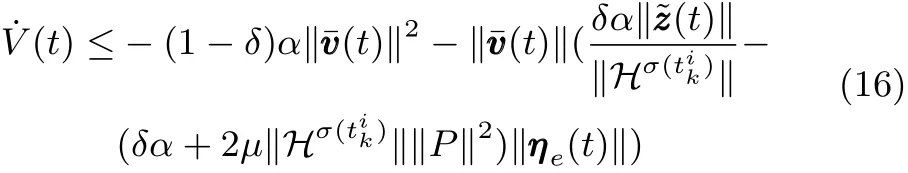
在区间[tik,tik+1)中,事件触发条件总是满足

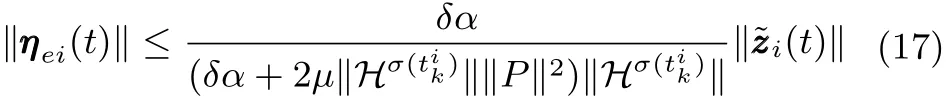
可以得到事件触发条件的紧缩形式为

将式(18)代入式(16),可以得到

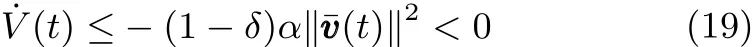
注 3. 事件触发条件通过一个安装在智能体上的嵌入式微处理器进行判断.若智能体会向邻居节点传送当前时刻的观测值否则,不传递信息.

在有限时间内发生无限次触发的情况被称为芝诺现象.若芝诺现象产生,则认为设计的事件触发传输机制不可行.为了排除芝诺现象,需要计算最小事件触发间隔时间,当最小触发间隔时间大于零时,芝诺现象被排除.

首先,对‖ηei(t)‖和‖˜zi(t)‖在区间内进行求导,可以得到

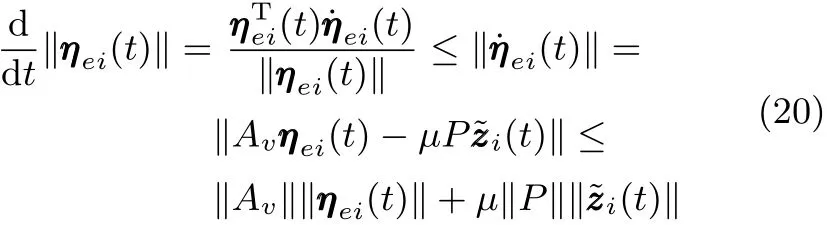
和

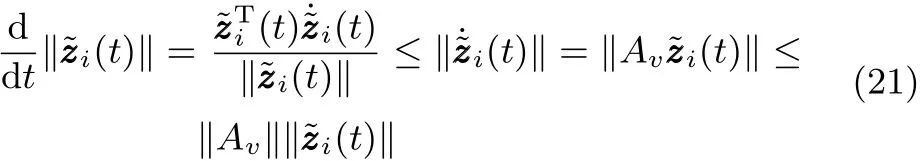
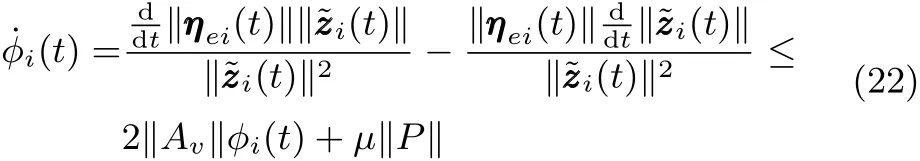
且 φi(t)满足其中是方程

下面,在定理 1的基础上,考虑智能体状态不可直接测量的情况,提出了一种基于输出反馈的事件触发控制机制.设计输出调节控制协议为

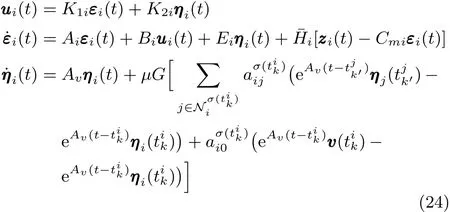
其中 εi(t)∈Rni为智能体状态的观测值,K1i∈Rki×ni, K2i∈Rki×q为反馈增益矩阵,为待设计的增益矩阵.

考虑在控制器(24)作用下的多智能体系统(5),闭环子系统可以表示为

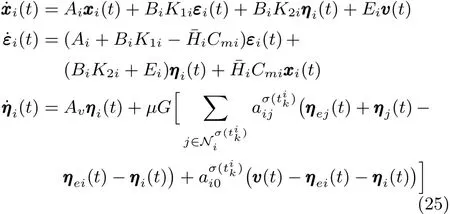
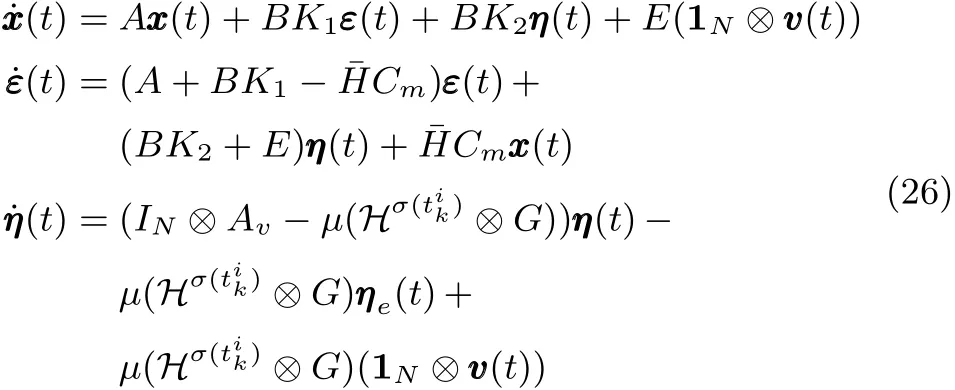
定理 2.如果假设 1～4满足.参数 µ,γ,σ,α和增益G在定理1中定义.事件触发条件为(9).找到增益矩阵K1i和 ¯Hi使Ai+BiK1i和Ai−¯HiCmi为Hurwitz矩阵, K2i=Ui−K1iXi.在控制器(24)的作用下,多智能体系统(2)能够实现协同输出调节,当且仅当如下等式满足

和

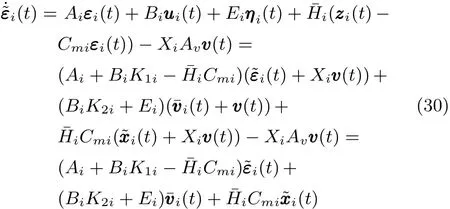
智能体的调节输出可以写成

3 仿真实例

考虑由4个智能体和1个外部系统组成的多智能体系统,智能体的动态方程为[18]

给定µ=0.2,σ=0.7,α=1,对Ricatti方程进行求解,可以得到P=I2.对式(27)进行求解,可以得到Xi=由于控制器增益矩阵满足 Ai+BiK1i和为 Hurwitz矩阵,可以取K1i=[−2−2−2],

通过图1和图2可以看出智能体的调节输出ei(t)能够渐近趋于零,也就是说多智能体系统能够实现对外部系统的状态跟踪和干扰抑制.图3表示事件触发间隔时间和事件触发时刻,可以看出平均触发间隔时间为0.8840s,平均触发次数为57次.

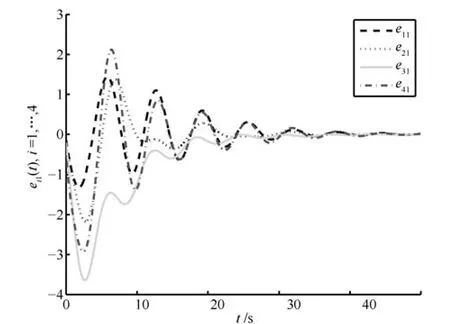
图1 智能体的调节输出ei1(t),i=1,···,4Fig.1 Regulated outputs ei1(t),i=1,···,4

4 结论

本文设计了基于事件触发的输出调节控制器,并对控制器参数进行确定.在本文提出的控制器的作用下,异构多智能体系统能够实现对外部系统的渐近跟踪和干扰抑制.此外,智能体之间的信息传递数量将会降低,从而降低通信负载减少网络能耗.接下来将进一步研究基于事件触发传输机制的不确定线性系统输出调节问题.

图2 智能体的调节输出ei2(t),i=1,···,4Fig.2 Regulated outputs ei2(t),i=1,···,4

图3 智能体的事件触发时刻和事件触发间隔时间Fig.3 Event instants and interval times

1 Huang J.Nonlinear Output Regulation:Theory and Applications.Philadelphia:SIAM,2004.

2 Wang Xing-Ping,Song Yan-Rong,Cheng Zhao-Lin.Exponential synchronization of time-varying linear multi-agent systems with switching topology.Acta Automatica Sinica, 2015,41(8):1528−1532 (王兴平,宋艳荣,程兆林.切换网络下时变线性多智能体系统的指数同步.自动化学报,2015,41(8):1528−1532)

3 Guo G,Ding L,Han Q L.A distributed event-triggered transmission strategy for sampled-data consensus of multiagent systems.Automatica,2014,50(5):1489−1496

4 Tang Y,Gao H J,Zhang W B,Kurths J.Leader-following consensus of a class of stochastic delayed multi-agent systems with partial mixed impulses.Automatica,2015,53: 346−354

5 Wang G,Shen Y.Second-order cluster consensus of multiagent dynamical systems with impulsive e ff ects.Communications in Nonlinear Science and Numerical Simulation, 2014,19(9):3220−3228

6 Zhou Feng,Wu Yan-Xuan.Consensus tracking algorithms with directed network.Acta Automatica Sinica,2015,41(1): 180−185 (周峰,吴炎烜.基于有向网络的一致性跟踪算法.自动化学报,2015, 41(1):180−185)

7 Li H J,Su H Y.Second-order consensus in multi-agent systems with directed topologies and communication constraints.Neurocomputing,2016,173:942−952

8 Xia Y Q,Na X T,Sun Z Q,Chen J.Formation control and collision avoidance for multi-agent systems based on position estimation.ISA Transactions,2016,61:287−296

9 Luo Xiao-Yuan,Yang Fan,Li Shao-Bao,Guan Xin-Ping. Generation of optimally persistent formation for multi-agent systems.Acta Automatica Sinica,2014,40(7):1311−1319 (罗小元,杨帆,李绍宝,关新平.多智能体系统的最优持久编队生成策略.自动化学报,2014,40(7):1311−1319)

10 Fax J A,Murray R M.Information fl ow and cooperative control of vehicle formations.IEEE Transactions on Automatic Control,2004,49(9):1465−1476

11 Wang X L,Hong Y G,Huang J,Jiang Z P.A distributed control approach to a robust output regulation problem for multi-agent linear systems.IEEE Transactions on Automatic Control,2010,55(12):2891−2895

12 Su Y F,Huang J.Cooperative output regulation of linear multi-agent systems.IEEE Transactions on Automatic Control,2012,57(4):1062−1066

13 Tang Y T,Hong Y G,Wang X H.Distributed output regulation for a class of nonlinear multi-agent systems with unknown-input leaders.Automatica,2015,62:154−160

14 You Ke-You,Xie Li-Hua.Survey of recent progress in networked control systems.Acta Automatica Sinica,2013, 39(2):101−118 (游科友,谢立华.网络控制系统的最新研究综述.自动化学报,2013, 39(2):101−118)

15 Zhu Chao-Qun,Guo Ge.Optimal control for event-triggered networked control systems.Control and Decision,2014, 29(5):802−808 (祝超群,郭戈.事件驱动的网络化系统最优控制.控制与决策,2014, 29(5):802−808)

16 Wang X L,Ni W,Ma Z B.Distributed event-triggered output regulation of multi-agent systems.International Journal of Control,2015,88(3):640−652

17 Hu W F,Liu L.Cooperative output regulation of heterogeneous linear multi-agent systems by event-triggered control. IEEE Transactions on Cybernetics,2017,4(1):105−116

18 Wieland P,Sepulchre R,Allg¨ower F.An internal model principle is necessary and sufficient for linear output synchronization.Automatica,2011,47(5):1068−1074

杨若涵 同济大学控制科学与工程系硕士研究生.主要研究方向为多智能体系统和网络控制系统.E-mail:xh-yrh@163.com

(YANG Ruo-Han Master student in the Department of Control Science and Engineering,Tongji University.Her research interest covers multi-agent systems and networked control systems.)

张 皓 同济大学控制科学与工程系教授.主要研究方向为复杂网络，网络控制系统，多智能体系统和切换系统.本文通信作者.

E-mail:zhang hao@tongji.edu.cn

(ZHANG Hao Professor in the Department of Control Science and Engineering,Tongji University.Her research interest covers complex networks,network-based control systems,multiagent systems,and switching systems.Corresponding author of this paper.)

严怀成 华东理工大学信息科学与工程学院教授.主要研究方向为网络化控制系统,鲁棒控制和随机系统.

E-mail:hcyan@ecust.edu.cn

(YAN Huai-Cheng Professor at the School of Information Science and Engineering,East China University of Science and Technology.His research interest covers networked control systems,robust control,and stochastic systems.)

Event-triggered Cooperative Output Regulation of Heterogeneous Multi-agent Systems with Switching Topology

YANG Ruo-Han1ZHANG Hao1YAN Huai-Cheng2,3

This paper studies the cooperative output regulation problem for multi-agent systems with switching topology.A novel event-triggered control scheme is designed,which can reduce communication load and save network energy.It is shown that under the proposed control strategy,agents can achieve asymptotic tracking and disturbance rejection.Finally,an example is presented to illustrate the e ff ectiveness of main results.

Heterogeneous multi-agent systems,cooperative output regulation,event-triggered control,switching topologies

杨若涵,张皓,严怀成.基于事件触发的拓扑切换异构多智能体协同输出调节.自动化学报,2017,43(3):472−477

YangRuo-Han,ZhangHao,YanHuai-Cheng. Event-triggered cooperative output regulation of heterogeneous multi-agent systems with switching topology.Acta Automatica Sinica,2017,43(3):472−477

2016-04-01 录用日期2016-08-02

Manuscript received April 1,2016;accepted August 2,2016

国家自然科学基金 (61272064,61273026,61673178),上海浦江计划(14PJ1409000),上海曙光计划(16GS28)资助

Supported by National Natural Science Foundation of China (61272064,61273026,61673178),ShanghaiPujiang Program (14PJ1409000),Shanghai Shuguang Program(16GS28)

本文责任编委 洪奕光

Recommended by Associate Editor HONG Yi-Guang

1.同济大学电子与信息工程学院控制科学与工程系上海 200092 2.华东理工大学化工过程先进控制和优化技术教育部重点实验室 上海 200237 3.华东理工大学信息科学与工程学院上海200237

1.Department of Control Science and Engineering,Tongji University,Shanghai 200092 2.Key Laboratory of Advanced Control and Optimization for Chemical Process of Ministry of Education, East China University of Science and Technology,Shanghai 200237 3.School of Information Science and Engineering,East China University of Science and Technology,Shanghai 200237

DOI10.16383/j.aas.2017.c160304