思维的增量在哪里
———以《20以内退位减法》复习课为例
2017-03-31孙其英
孙其英
小学生学习数学的过程是一个不断再创造,形成新的知识结构,并促进思维能力螺旋上升的过程。在这个过程中,每一节数学课的思维增量,支撑着学生思维能力的提高。
一、在学生想不到的地方设计问题,锻炼思维的全面性
课堂片断一:课始,出示()-7=比6大,填填看,你是怎么想的?
学生纷纷进行填写,反馈有两种想法:
生1:填一个数字,算一算,看差是不是比6大,所以,填写了 17、14、16 等。
生2:我也是,一开始试了10、13,发现差没有比6大,后面试的都可以。
学生想不到的地方:一年级的学生思维还处于感性思维占主体阶段,尝试法是他们学习数学常用的方法,在这个练习中,学生利用尝试法进行计算,得出结果。可以从几开始想,答案有几个,要注意什么,这些都是学生想不到的地方。
教学策略:针对学生的思维特点,设计问题:从几开始写?要注意什么?
课堂再现:
问题1:从几开始写?
师:刚才报了好多答案,那么,从几开始写呢?
生1:从14开始写。我是从差开始想的,因为差要比6大,可以是7、8、9……,( )-7=7、( )-7=8、( )-7=9……所以,被减数就是 14、15、16……
生2:先写13,我是与13-7=6进行对比,因为差要比6大,所以,被减数13是不够的,那可以是 14、15、16……,所以,从 14 开始写。
问题2:要注意什么?
将( )-7=比6大过渡到( )-7>6,并出示13-()>6,填填看,从几开始填?
生1:从6开始填。我想答案要大于6,可以是 7、8、9 等,13-()=7,13-()=8,13-()=9,就可以得出()从6开始填。
生2:从6开始填。我是与13-7=6进行比较,答案比6大,也就是减去的数要比7小,可以从6开始填写。
师:要注意什么?
生3:要注意不要漏掉0,应该是6~0。
生4:是的,我刚才就是6~1。
【教学思考:问题“从几开始写”,让学生的思维趋于有序,一开始的尝试填写,从无序填写,到有序思考,是思维上的一个跨越。通过问题“要注意什么”,提醒学生要注意容易漏掉的“0”,使思维更趋于完整、全面。通过看似平常的两个问题,在学生想不到的地方,关注了思维的有序性,关注了“0”这个易漏点,让学生的思维经历从一开始的无序到有序,从随意到严谨,做到不重复、不遗漏。】
二、在学生想不深的地方资源链接,培养思维的深刻性
课堂片断二:出示()-()=6,你有什么发现?
生1:7-1=6开始填写,一直到20-14=6。
生 2:20-14=6,一直到 7-1=6。
生3:还有6-0=6,不能漏掉。
师:你有什么发现吗?
生4:被减数有规律,减数有规律。
教学策略:学生对单列数据已经感悟到填写规律,但不能深入思考算式整体之间的关系。这时,我采用资源链接法,用数形结合和生活中的年龄问题来帮助学生深入思考。
课堂再现:
师:这类问题比较抽象,让图形来帮助我们吧。
链接1:数形结合。

图1
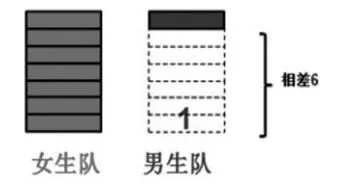
图2
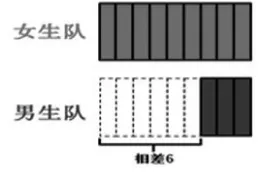
图3
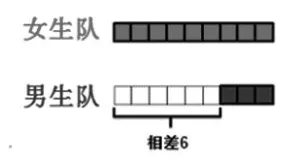
图4
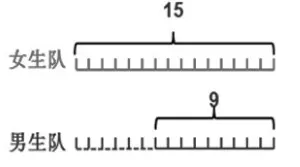
图5

图6
从图1到图2,用长方形表示,两个队始终相差6,我们可以继续表示一直到20-14=6;从图2到图3,把长方形竖起来,两个队还是相差6;从图3到图4,把长方形压扁,变成小正方形,仍旧表示两个队相差6;从图4到图5,继续压扁,变成两根线段,还是表示两个队相差6;从图5到图6,将相差部分从左边移到右边,也是表示相差6。
链接2:年龄问题。
师:( )-( )=6,还可以怎样想呢?让生活经验来帮我们理解吧!
出示一组班级中小朋友的姐弟照片,出示他们的年龄:

师:他们都可以用( )-( )=6来表示,这就是生活中的数学问题。那么,小明10岁时,姐姐几岁呢?姐姐20岁时,小明几岁呢?
生:小明10岁时,姐姐16岁,因为(16)-(10)=6;姐姐20岁时,小明14岁,因为(20)-(14)=6。
【教学思考:从长方形到压扁的小正方形,再到线段,是一个渐进的过程,也是从平面图形到线段的抽象过程,为今后的线段图学习奠定基础。数学源于生活,生活中处处有数学。年龄是学生的生活经验,迁移生活经验来理解抽象的()-()=6,让学生感受到数学不再是抽象的。在学生想不深的地方,运用资源链接,数形结合,迁移生活经验,锻炼思维的深刻性,思维就有了增量。】
三、在学生想不透的地方渗透代数结构,促进思维的灵活性
课堂片断三:出示13-7=( )-6,你是怎么想的?
生 1:因为 7-1=8-2=9-3=……=6,所以,括号里填12。
生2:因为左边等于6,右边也要等于6,所以,括号里填12。
师:对了,这样的题目我们以前叫它“火车车厢”算式(即将算式看成是一节“车厢”,每节车厢得数相等,类似天平原理),那你能填写下面这题吗?
出示:( )-7=( )-6,你有什么发现?
生3:根据“火车车厢”原理填的,两边都等于6,所以,填 13 和 12。
师:还有其他的吗?
(学生进入思考,一时没人举手)
教学策略:像这一类比较抽象的等式问题,我采用渗透代数结构的方法,促进学生思维的灵活性。
课堂再现:
师:除了两边都等于6,还可以等于其他数吗?
生1:可以等于5,那就填12、11,也可以等于其他数。
师:还可以怎么想?
生2:还可以这样想,减数7到6减少了1,那被减数也减少1就好了,所以,只要是第一个被减数比第二个被减数大1的,都可以。
师:说得真好!要解决( )-7=()-6,不仅可以考虑等号两边的关系,还可以考虑减数之间的规律导致被减数之间的规律,因为减数少1,要使差相等,被减数也要少1。这种从算式的结构角度去思考,叫代数结构思维,是系统解决问题的好办法。
【教学思考:要解决( )-7=( )-6,不仅是一种逆向思维,要考虑等号两边的关系,还要考虑减数之间的规律导致被减数之间的规律,才能灵活地进行解决,这正是学生想不透的地方。从考虑数的规律到考虑算式整体的规律,学生的思维有了一定的增量,那么学生的思维就灵活了。】
