借助直观理解变形——《解方程》教学片断与解读

李春英（特级教师）

从上世纪七十年代末小学阶段引入解方程以来，解方程教学大致可以分为三个阶段。第一阶段是用四则运算关系解方程，就是熟练运用四则运算中各部分之间的关系去解方程。第二阶段是2001版课标中提倡的用等式性质解方程。第三阶段是2011版《课程标准》中明确“用等式的性质解简单的方程”的要求。这个过程体现了从算术思维到代数思维的转变。

让学生经历从用四则运算关系解方程到用等式性质解方程的过程，或者是通过两种解方程的思路来达到二者之间的沟通与融合，从而让学生顺利地把四则运算关系与等式性质建立起联系，用等式的性质来解释四则运算关系，用四则运算关系来验证等式的性质。如果能够实现这个沟通，那么就能够很好地解决解方程教学中“非此即彼”的教学实际问题，在算术思维解方程和代数思维解方程之间架起一座桥梁，让它们彼此“握手言欢”。本节课的教学设计试图以此为突破口，尝试借助天平直观沟通二者之间的联系，体会方程变形的不同依据，突出等式性质的一般性和优越性。

【教学片断与解读】

一、利用游戏，引入新课，从不等式到等式（从图到式）

1.你会用含有字母的式子表示吗？

小结：从左向右看用“＜”来连接，从右向左看用“＞”来连接。

2.你会用含有字母的式子表示吗？

小结：等式的两边虽然都只有一个字母，但也是方程。

3.这个天平图能用方程式表示吗？是方程吗？为什么？

为了讨论方便，老师把这三个图形所表示的重量分别用a、b、c代替。它们之间的关系可以表示为a=b+c，也可以表示为b+c=a。刚才有同学写的是a-b=c，可以吗？

小结：天平图示表示的等量关系是a=b+c，同学们想到的减法数量关系是经过你们推理得到的，也就是说天平两边同时减去b或者c得到的。所以图示不同，方程式也不同。

【解读：从不等式到等式，突出天平的平衡原理，丰富学生对方程意义的理解。通过x=y这种形式渗透方程的对称性。通过沟通不同天平图示之间的联系，复习等式的基本性质，并把等式的基本性质与学生的推理结合起来，初步沟通等式的基本性质与四则运算各部分关系之间的联系。】

二、借助天平，体会变形，从等式到等式（式图结合）

1.你知道 a、b、c 这三个未知数的值可能是多少吗？有多少种可能？依据是什么？

如果老师告诉你a=100，你知道b和c是多少吗？如果老师告诉你b=35呢，你可以求出c的值吗？怎么求？根据是什么？

小结：同学们刚才根据天平图示写出来的方程式其实就是一个等量关系式。不管有多少种可能，都不能离开这个等量关系式去假设。

2.你能很快说出这些方程中x的值吗？根据是什么？

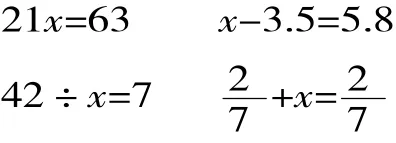
【解读：追问“可能是多少”的目的是进一步体会方程本身就是一种等量关系，就是一个模型。不论三个未知数可能是多少，都不能离开原有的这个模型。四道小题学生根据以往的推算经验，很快就能说出x的值。它有三个作用，一是可以复习四则运算中各部分之间的关系；二是可以和复杂方程进行对比，激发学生学习用等式基本性质解方程的兴趣；三是为学生探究用等式基本性质解方程提供简单的学习材料。】

3.（出示8-2x=9-4x）这道题你还能很快说出x的值吗？为什么？怎么办呢？

老师把这个方程放到平衡的天平上，可以根据什么来求x的值？请你检查一下天平的每一次变化之后是否还平衡？根据是什么？同桌交流。

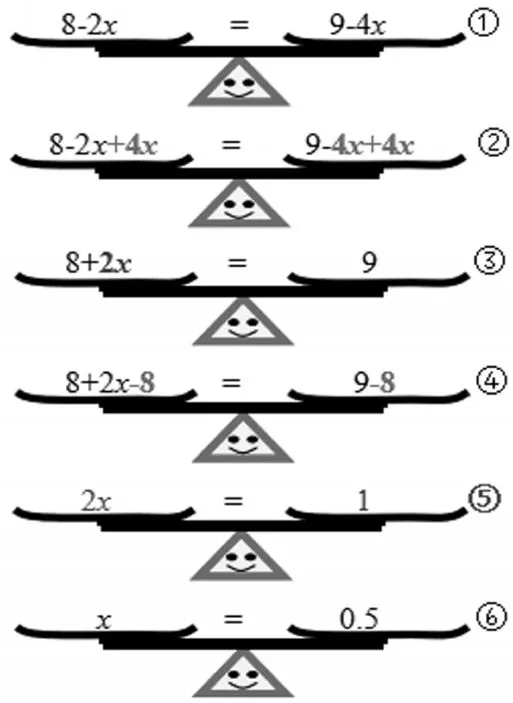
反馈交流。平衡吗？为什么？

①—②方程两边都加4x，平衡。

②—③化简得到，平衡。

③—④方程两边都减8，平衡。

④—⑤化简得到，平衡。

⑤—⑥方程两边都除以2，平衡。

小结：同学们借助天平图示，能看懂并说清每一次变化的依据，用等式的性质解释天平的每一次变化。太棒了！

【解读：这是一个比较复杂的方程，学生用惯性思维找不到各部分之间的关系，无法用已有的经验顺利解决，从而引起其认知冲突，激发学习另一种解方程方法的兴趣，为学生主动探究用等式基本性质解方程提供内驱力支撑。教师给出天平，在天平的直观支撑下看懂每一次变化后的天平图示，激活学生已有的等式性质的知识，体会等式性质在解方程过程中的一般性和优越性。】

4.把天平图示去掉，你还能说出方程每一步变形的依据吗？

小结：当我们一时看不出方程各部分的关系时，可用等式的性质通过方程变形求出未知数x的值。看来等式的性质也是我们求解未知数值的好帮手。

观察整个求未知数x的过程，如果把这个方程看作一个绳上的套，那么我们就是在用等式的性质一步步地把方程这个套解开，因此我们把这个叫做解方程。在解方程之前要先在方程左边写上一个“解”字，后面点上“：”这个标点符号，表示你要开始解这个“套”了。

从解方程的过程中，你还能发现需要注意什么吗？

小结：等号对齐，表示天平依然保持平衡，结果仍然是等式。开头写“解”，等号对齐，是解方程的两个格式要求。

【解读：在学生初步体会运用等式性质解方程的必要性之后，把解方程的过程从天平图示中抽离出来，通过回顾等式的性质完成对解方程的整体感知。通过观察完整解方程的过程，强调解方程的两个格式：开头写“解”，等号对齐，比较形象直观地进行格式要求。为学生主动探究用等式基本性质解方程提供外在的技术支撑。】

三、自主探究，沟通联系，从复杂到简单（从式到图）

1.现在请同学们尝试着用等式的基本性质解方程。我们先从最简单的方程开始研究。

请你先在每个方程下面画出天平，用等式的性质解下面的方程。注意格式哦！

①35+x=100②x-3.5=5.8

③5x=80④42÷x=7

2.反馈交流：实物投影展示学生作品，先学生汇报再集体交流。

①两边都减35，平衡；左边剩 x，右边是 100-35；x=100-35，其实就是和减去一个加数。

②两边都加3.5，平衡；左边剩x，右边是5.8+3.5，其实就是差加上减数。

③两边都除以5，平衡；左边剩 x，右边是 80÷5，其实就是积除以一个因数。

④两边都乘 x，变形为42=7x，平衡；通常将含有未知数的代数式写在方程左边，变形为7x=42，与第③题一样。

【解读：这个环节化繁为简，让学生用最简单的方程体会最基本的变形。因为有了前面观察天平图示变化过程以及没有天平图示方程的变化过程，学生已经积累了一定的用等式性质使方程变形的基本经验。要求学生在方程的下面画天平图的目的在于直观地理解两边同时加、减、乘或除使最后天平左边只剩x。通过观察和分析，得出等式的基本性质与各部分关系之间及两种解方程方法之间的联系。实现这个环节目标的前提是学生对等式性质和四则运算之间关系的表述清楚明白，否则这个环节的目标就无法达成。因此学生的语言表达在这个环节显得尤为重要。】

3.观察这四个方程解的过程，它们有什么共同点？

①都可以用等式的性质，也可以用各部分关系。

②都想办法让等号的左边只剩下x。

③开始都要写一个“解”字，然后写“：”。

④每一步的等号都要对齐。

不论用哪一种方法解方程，我们都要把方程变形为“x=？”的形式。

4.我们把这个结果叫做方程的解。请你用“x=（）是方程（）的解”说一说这四道题目。

想一想方程的解和解方程是一回事吗？

小结：解方程是一个过程，是求方程的解的过程。方程的解是一个数，是未知数的值。

5.跟踪练习：看图列方程，并求方程的解。说一说每一步的依据是什么？用等式的性质和四则运算之间的关系这两种方法来解释。

四、巩固方法，学会检验，从具体到抽象（有式无图）

1.没有天平图的帮助，你会解下面的方程吗？还能说出解这个方程每一步的依据吗？

解方程：18（x+14）=540

遇到有括号的方程怎么办？

把括号里的数即“x+14”的和看作一个整体。如果老师把题目变成 5（12+x）=8x，你还能把括号看作一个整体吗？为什么？

小结：很多时候括号是不能看作一个整体的，我们要根据具体数字的特点灵活判断。

2.求出来的x的值是这个方程的解吗？这就需要我们对这个数进行检验。

你能想出检验的方法吗？请打开书第102页，看例1和例2的检验方法，用笔圈起来。

检测：18×（16+14）=540

小结：通过把16代入原方程检验，我们知道x=16可以使这个方程的左右两边相等，我们就把x=16这个x的值叫作这个方程的解。

3.用书上的检验方法判断并说明原因，要求说完整。

（1）x+32=76（x=44，x=108）

（2）12-x=4 （x=16，x=8）

（3）4x=6（x=1.5，x=2）

（4）3÷x=1.5（x=0.5，x=2）

学生解答：

（1）因为 44+32=76，所以x=44是方程的解。

（2）因为 12-8=4，所以 x=8是方程的解。

（3）因为4×1.5=6，所以x=1.5是方程的解。

（4）因为3÷2=1.5，所以x=2是方程的解。

小结：只有使方程左右两边相等的未知数的值才是这个方程的解。

【解读：方程的解这个概念其实并不容易理解。本节课分两次进行教学。第一次是在尝试用等式性质解方程环节，通过让学生读一读x=（）的形式感悟方程的解是一个数，通过说一说x=（）是方程（）的解，体会不同方程的解是不同的。第二次是在检验环节，通过把x的值代入原方程检验的方法，进一步加深方程的解是一个能使方程左右两边相等的未知数的值。最后通过一个检验题目完善方程的解的概念。】

五、拓展练习，综合运用，从单一到综合（有图无式）

1.看图列方程，并求出方程的解。

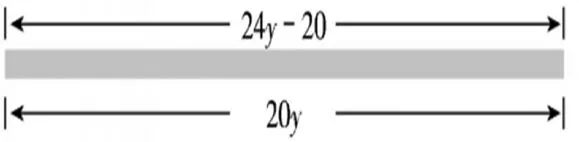
2.看图编一道实际应用题。

【解读：解方程是为了解决实际问题。除了天平这个模型之外，还有线段相等、面积相等、距离相等、速度相等，等等。这些等量关系帮助我们用相等的思路列出方程，然后利用等式的基本性质或者四则运算中各部分之间的关系求出x的值，从而顺利解决问题。这两道题目只是提供了线段相等的模型，起到拓展思路的作用。】