“自动控制原理”课程的传递函数概念部分教学探讨

王家林+杨宣访+肖良芬+杨忠林

【摘 要】 本文对“自动控制原理”课程中传递函数概念部分内容的教学进行了探讨。笔者讨论了系统传递函数概念部分的特点和教学难点，并列举了教学中普遍存在的问题，归纳出产生这些问题的潜在原因，并从这些潜在原因入手，有针对性提出了一些教学方法和建议。

【关键词】 自动控制原理；传递函数概念部分；课程教学

【Abstract】 This paper investigates the teaching for the conception of transfer function part of Automatic Control course. Firstly， the characteristics of contents and the teaching difficulties in the conception of transfer function Part are discussed， and the common existing problems encountered in teaching are listed. Secondly， the potential reasons for these existing problems are summarized. To solve these common teaching problems， we propose some teaching methods and sug-gestions according to the potential reasons. Finally， by employing a teaching example， we also show how to well apply the teaching methods proposed above.

【Key Words】 principle of automatic control； the conception of transfer function； course teaching

【中图分类号】 G642.0 【文献标识码】 A 【文章编号】 2095-3089（2016）36-00-01

“自动控制原理”是一门工程性很强的专业基础课程，它是自动控制技术的理论基础，自动控制技术有着非常广泛的应用，现已成为国内外高校工科专业普遍开设的课程。该课程具有数学公式较多，抽象的理论、概念多等特点，学生学习具有一定的深度和难度。目前，文献研究主要集中在对“自动控制原理”整个课程的教学探讨上，很少有专门针对某一章节或某一知识点而讨论其具体存在的教学问题，以及相对应的解决策略[1-5]。在“自动控制原理”的教学中，传递函数是描述线性系统动态特性的基本数学工具之一，经典控制理论的主要研究方法——频率分析法和根轨迹法，都是建立在传递函数的基础之上。传递函数是研究经典控制理论的主要工具之一。而学生对传递函数的概念，定义及性质的理解和掌握程度，直接影响着后续学习的效果。笔者针对“自动控制原理”传递函数概念教学部分，总结出了目前关于这一部分教与学中较为常见的几个问题，探讨并提出了一些见解和具体的讲授方法。

1 传递函数概念部分教与学的现状

控制系统传递函数概念部分主要包括传递函数的定义。这部分内容从授课角度而言，内容看似非常简单，数学知识点较少，但在讲授的趣味性和知识的系统性上较难把握；同时很多学生反映有些基本概念并不复杂，但较难理解透彻，特别是在“为什么”问题上容易纠结，影响学习效果。在传递函数定义的理解上具体可体现在以下几个方面：

传递函数的定义是线性定常系统在零初始条件下，输出信号的拉氏变换与输入信号的拉氏变换之比。就字面意思理解而言，并不复杂，特别是后面在使用传递的过程中，只需要计算输出信号的拉氏变换与输入信号的拉氏变换之比。然而，为什么要限定是线性定常系统呢？不是线性定常系统就不能定义传递函数了吗？零初始条件该怎么理解呢？不是零初始条件会怎么样呢？这几个问题对于讲授传递函数而言，都是需要明确的。如何讲授让学生能理解和掌握传递函数的概念定义是需要花上一番气力的。

2 传递函数概念部分的教学探讨

笔者针对上述教学中普遍存在的问题，建议采用如下有针对性的教学方法进行改进。

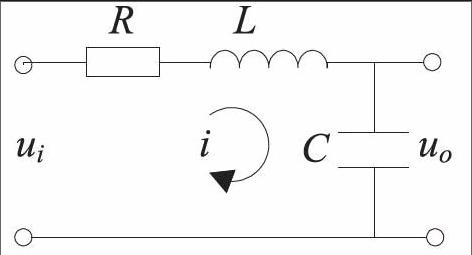
在讲授传递函数的定义时，会得到一个对初学者而言形式上较复杂的式子，式中为由系统结构和参数决定的常数。如何生动地让学生感受到传递函数的物理含义呢？我们可以用电路知识学习过的RLC电路来说明，用提问的方式引导学生思考如何利用定义求取系统的传递函数。RLC电路如图所示。

我们可以很快的得到其传递函数。通过对比RLC电路的传递函数和一般系统的通用传递函数表达式，使得学生掌握传递函数的求取方法，理解传递函数的参数是由系统结构和参数决定的。

至此，学生一般认为该知识点的内容已经结束，此时，抛出两个问题引发学生思考：

（1）为什么要限定是线性定常系统呢？

給出一个非线性定常系统的微分方程，，让学生求其传递函数，学生在求解过程中会发现，无法求得。此时，可以给出线性定常系统的一个重要性质：系统响应可表示为输入与系统单位脉冲响应的卷积。

换句话说：如何不是线性定常系统，就无法通过输出，输入信号求取出系统复域模型。

（2）零初始条件该怎么理解呢？

零初始条件包括两个方面的含义，可以从系统输入端和输出端来理解：

（a）对于输入量而言，零初始条件指的是输入量在时才作用于系统，即在输入及其各阶导数都为零。

（b）对于输出量而言，零初始条件指的是在输入量作用于系统之前，系统处于稳定的状态，在输出及其各阶导数都为零。以RLC电路为例，输出量的零初始条件指的就是L和C都没有储能。可以提问，为什么要L和C都没有储能呢？引发学生思考。

在讲解了零初始条件的含义的基础上，抛出问题：系统不是零初始条件会怎么样呢？此时可以让学生自己求取非零初始条件下的RLC电路传递函数。我们知道RLC电路系统的微分方程为：，非零初始条件下对微分方程取拉氏变换得，我们会发现系统不处于零初始条件，无法得到系统传递函数表达式，也就是说零初始条件是传递函数的应用条件。

3 结语

笔者根据以往的教学经验以及“自动控制原理”课程的特点，总结了该课程传递函数概念部分教学中普遍存在的问题，并讨论了这些问题存在的原因，阐述了如何运用所介绍的教学方法解决已有的教学问题。

参考文献：

[1]李长云.“自动控制理论”的系统化教学实践[J].电气电子教学学报，2013，35（4）：75-77

[2]崔明涛，过润秋，盛英，等.“自动控制原理”课程教学改革探究与实践[J].电气电子教学学报，2015，37（3）：24-26.

[3]孙建平，郭曼利.自动控制原理课程设计的改革与实践[J].中国现代教育装备，2015（225）：67-70.

[4]王柯，周延延，吴晓燕.“自动控制原理”课程实验教学改革与探索[J].中国电力教育（上），2013（34）：140-149.

[5]夏德钤，翁贻方.自动控制理论（第四版）[M].北京：机械工业出版社，2014.