超低频场强勒让德函数的导数表达式对比分析*

盖明明 温 东 郗海龙 楚 涓

(1.海军潜艇学院 青岛 266199)(2.北海舰队参谋部 青岛 266000)

超低频场强勒让德函数的导数表达式对比分析*

盖明明1温 东1郗海龙2楚 涓1

(1.海军潜艇学院 青岛 266199)(2.北海舰队参谋部 青岛 266000)

超低频电波大气场强计算中或包含第一类勒让德函数对距离的一阶导数或包含其二阶导数,这两个导数可以用无穷级数表示,但无穷级数计算受制于计算机的位数限制,因此在超低频的高端无法用级数计算。除此之外,还有几个近似表达公式。但近似公式的适用范围和精度尚不明确。所以基于Matlab软件对无穷级数公式和三个常见的近似公式进行编程计算,相互比较,以确定各个公式的适用条件和精度差别。

超低频; 大气场强; 勒让德函数对距离的一阶导数; 勒让德函数对距离的二阶导数

Class Number E962

1 引言

超低频发射天线目前主要是应用低架于地面上的两端接地的水平导线,作为这种天线的物理长度虽然很长(一般100km左右),但与波长相比仍很短,可以把它看作是水平电偶极子[1]。另外,地面上超低频电磁波在地面-电离层波导内发射和传播的,因此,超低频的辐射和传播问题,从数学上可以归纳为在圆球形地面-电离层波导内求解地面上水平电偶极子激发的电磁场问题。

在波导内,五个电磁场分量表达式中或包含第一类勒让德函数Pν0(-cosθ)对地心角θ(距离)的一阶导数,或包含其二阶导数。文献[2～4]中给出勒让德函数对距离的一阶导数和二阶导数的无穷级数公式的无穷级数形式为[2～4]

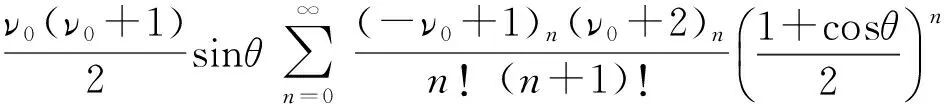
这两个导数可以用无穷级数表示,这是比较精确的表示。但遗憾的是,无穷级数计算受制于计算机的位数限制,一般的个人计算机浮点运算只提供小数点后15位精度,因此在超低频的高端无法用级数计算[1]。除此之外,还有对极点波表达式、平面波导表达式、驻波波导表达式等几个近似表达公式。但近似公式的适用范围尚不明确。所以基于Matlab软件对无穷级数公式和常见的三个近似公式进行编程计算,相互比较,以确定各个公式的适用条件。

2 勒让德函数对距离头二阶导数级数表达式与对极点波表达式对比分析

文献[2～3]给出了勒让德函数头二阶导数在对极点附近的近似表达式[2～3]

以白天为例,分别取频率30Hz、100Hz在距离0km～20000km范围进行仿真,如图1和图2所示,其中实线‘-’代表级数公式计算结果,点线‘-*’代表驻波公式计算结果。

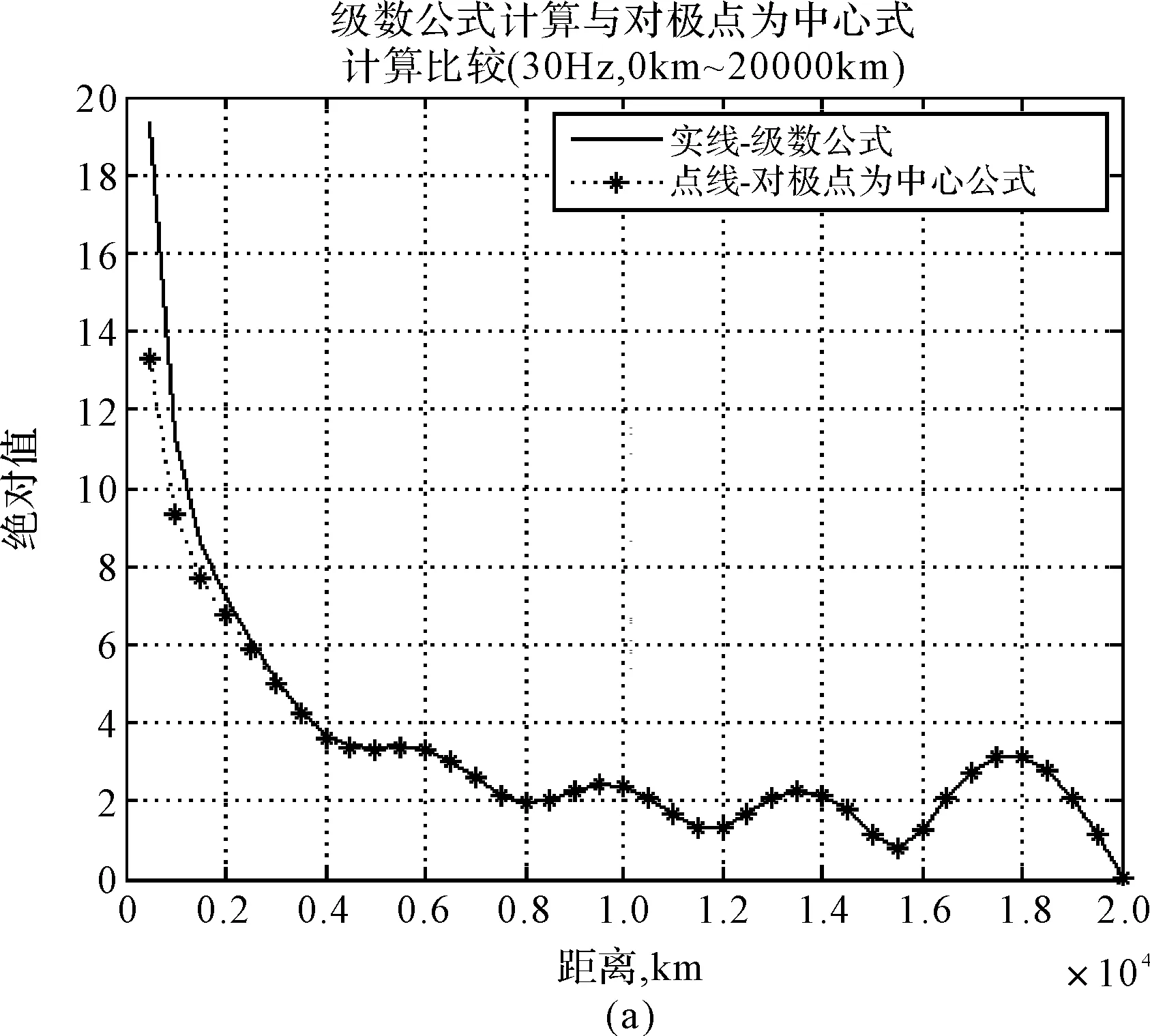
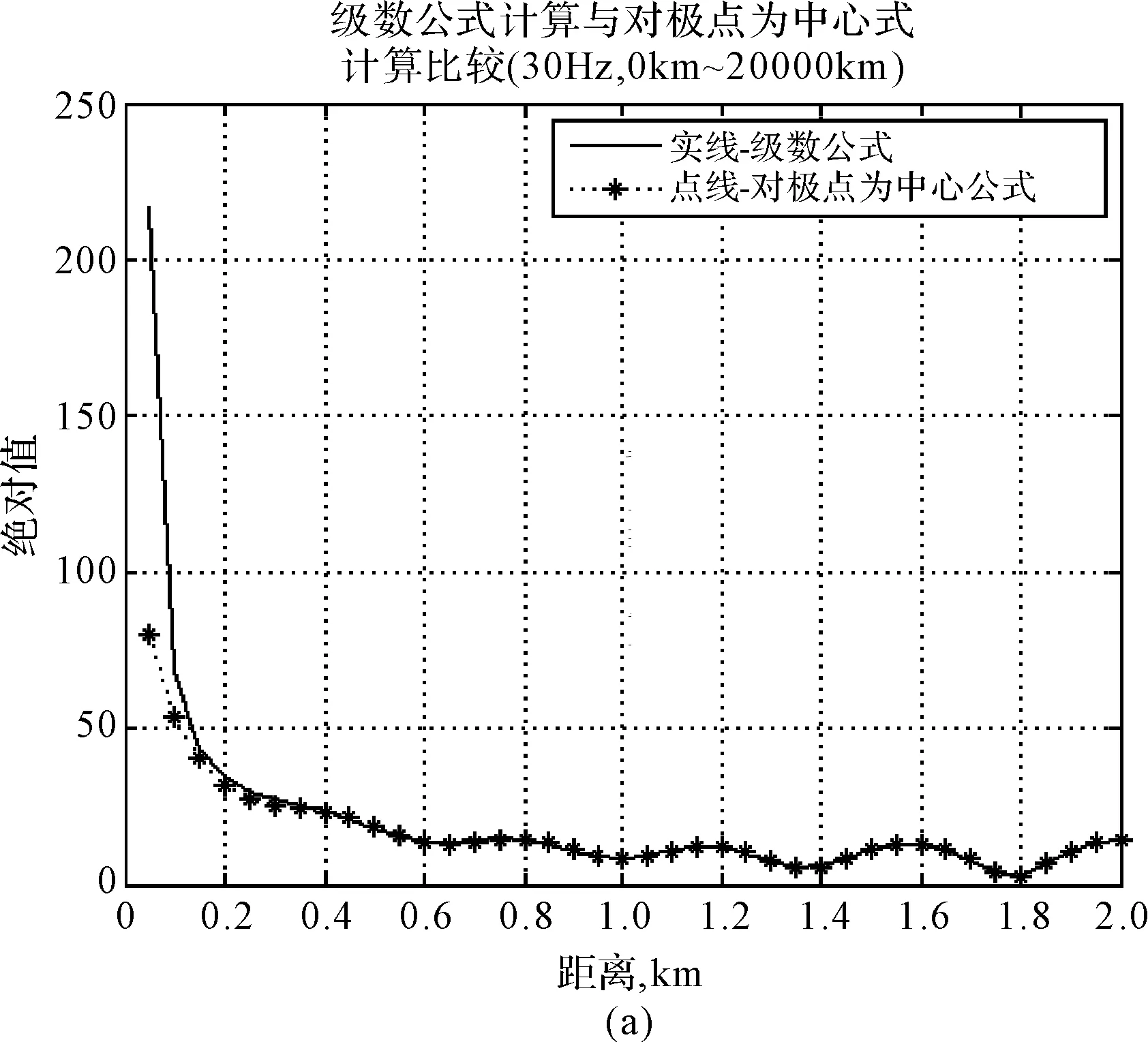
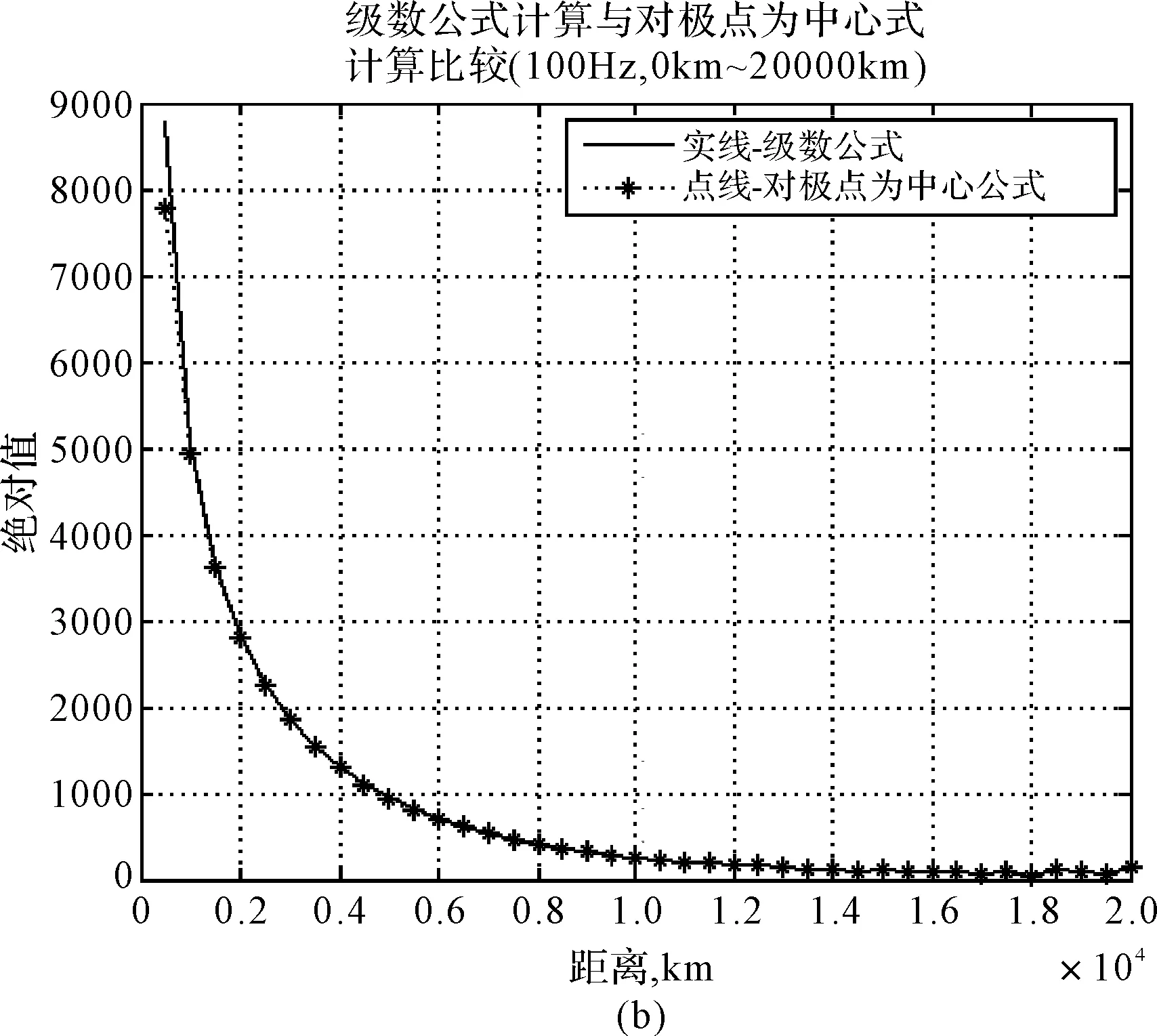
图2 勒让德函数对距离二阶导数级数表达式与对极点波表达式对比分析

图1和图2上示出级数公式和以对极点为中心公式计算的绝对值曲线的比较。其中图1(a)的频率是30Hz,两条曲线清晰地显示,大约在3000km以后,它们符合极好,3000km以内,以对极点为中心公式的数值小于级数公式。图1(b)上是100Hz的同样的曲线比较,图1(c)是图1(b)的部分曲线。从图1(b)、(c)这两张图可以清楚地看出,在大约1500km之后,两条曲线几乎完全一致,在大约1500km之内,以对极点为中心公式的值小于级数公式的值。这说明以对极点为中心公式的绝对值从离源点很近的距离开始直至对极点与级数公式的绝对值曲线符合十分良好,而且随频率的增高符合的近距离更缩短,符合的程度更接近。图2与图1只是在绝对值量级上大得多,而曲线趋势变化与一阶导数一致。

3 勒让德函数对距离头二阶导数级数表达式与平面波导表达式对比分析

文献[2～3]中给出勒让德函数头两阶导数平面近似公式如下[2～3]

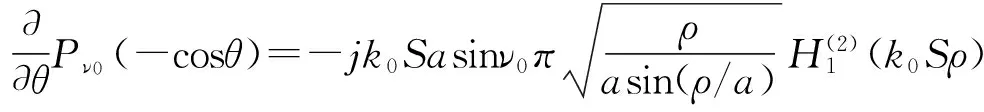
以白天为例,分别取频率30Hz、75Hz、100Hz和150Hz,在距离0km～20000km范围进行仿真,如图3和图4所示,其中实线‘-’代表级数公式计算结果,点线‘-*’代表驻波公式计算结果。

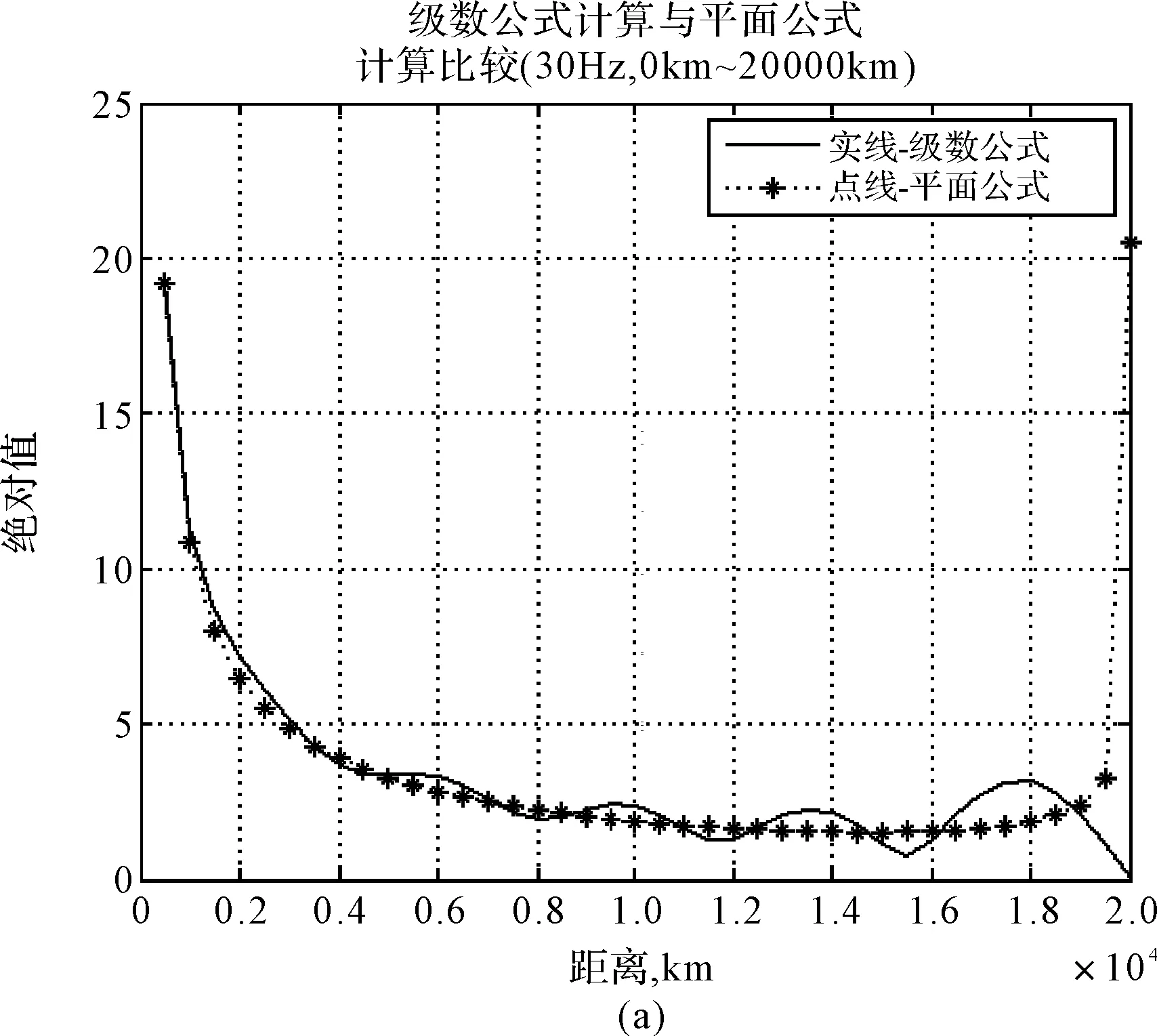
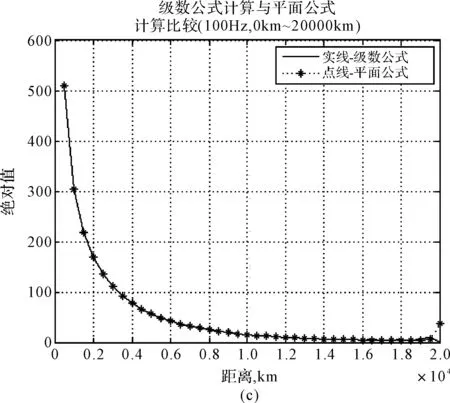
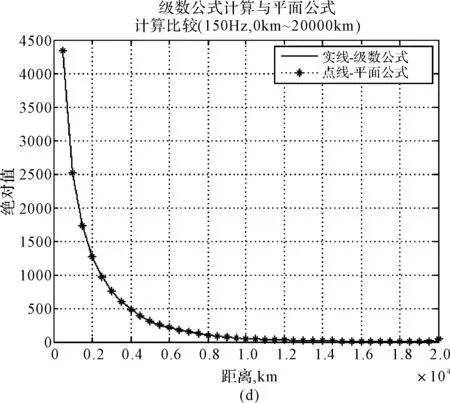
图3 勒让德函数对距离一阶导数级数表达式和平面波导表达式对比分析

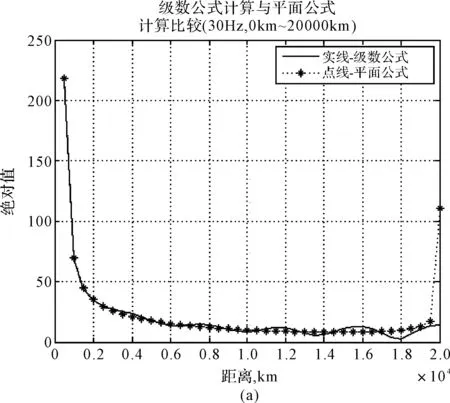
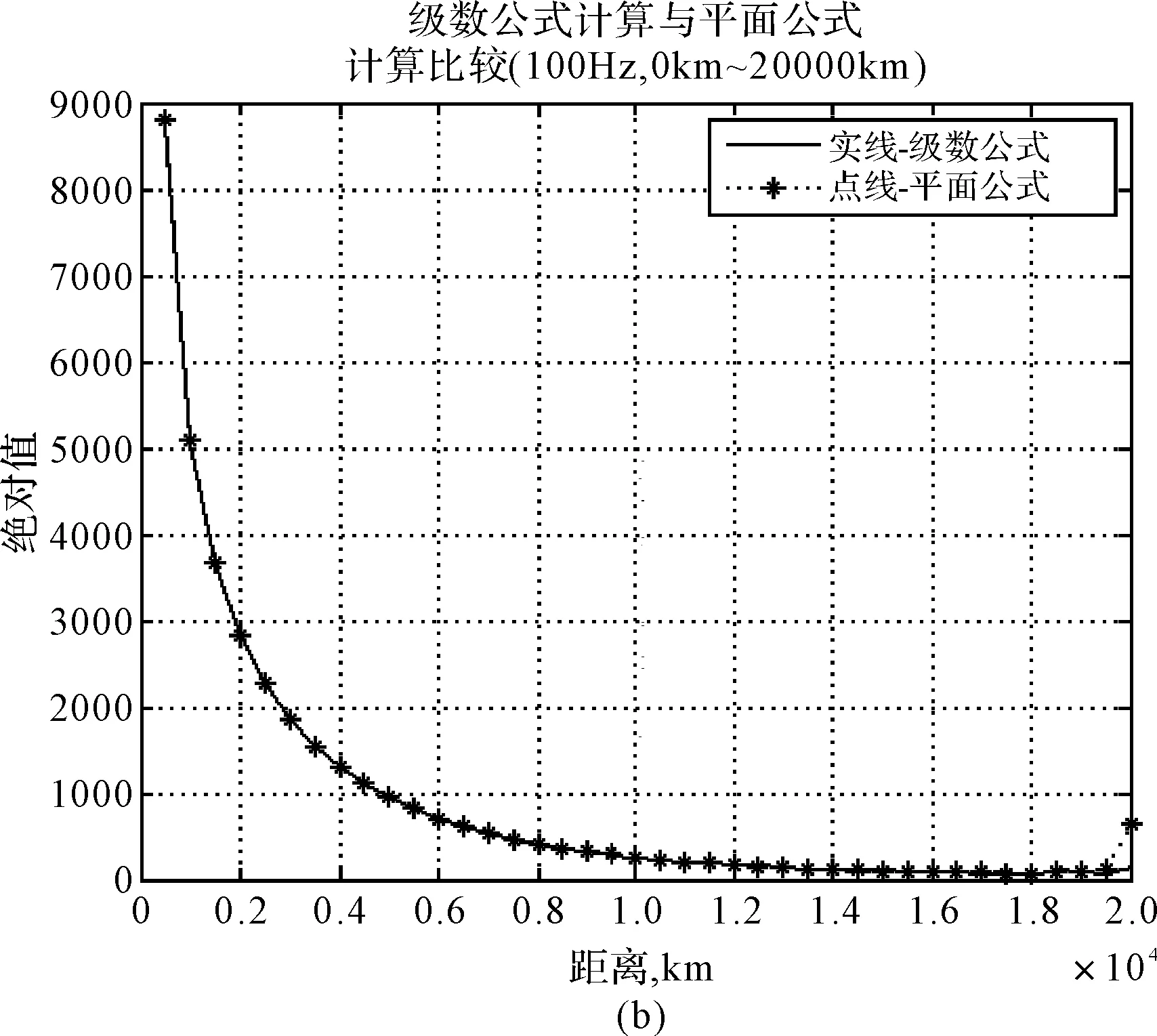
图4 勒让德函数对距离二阶导数级数表达式和平面波导表达式对比分析

图3(a)、(b)、(c)、(d)分别显示20000km之内30Hz、75Hz、100Hz和150Hz级数公式和平面公式计算的绝对值曲线。级数曲线有起伏,这是合理的,因为级数中包含直接波和非直接波,两个波的合成必然引起起伏。平面公式是一个行波,所以是平滑下降的斜线,但由于曲率修正因子的影响,所以接近对极点曲线迅速上升。这说明平面公式在对极点附近不能应用。在图3(a)上示出30Hz级数计算和平面公式计算绝对值曲线的比较。在近距离上,两条曲线的一致性比100Hz的差一点,而且符合良好的距离比100Hz的近得多,这是合理的,因为30Hz的衰减比100Hz的小得多,而150Hz符合度更好。图4与图3只是在绝对值量级上大得多,而曲线趋势变化与一阶导数一致。这些结果说明平面公式可以应用于较高频率,这个距离随频率增高而加大。

4 勒让德函数对距离头二阶导数级数表达式与驻波波导表达式对比分析

文献中给出勒让德函数头两阶导数的驻波公式,即两个往相反方向传播的行波公式的合成[2～3],即

+je-jk0Sρi]

因为二阶导数曲线变化趋势与一阶导数一致,只是在绝对值量级上比一阶导数大得多。所以选择白天,以发射频率为100Hz和30Hz的一阶导数为例,得到级数公式和驻波公式计算绝对值部分曲线的比较结果,如图5所示,其中黑色实线‘-’代表级数公式计算结果,点线‘-*’代表驻波公式计算结果。

从图5中看出,在大约2000km～19000km范围内,这两个公式的计算结果符合良好。在对极点附近,无论是100Hz还是30Hz驻波公式的绝对值都是急剧上升的,事实上电磁场在对极点不可能急剧上升的。在源点附近,驻波公式的绝对值小于级数公式的绝对值。

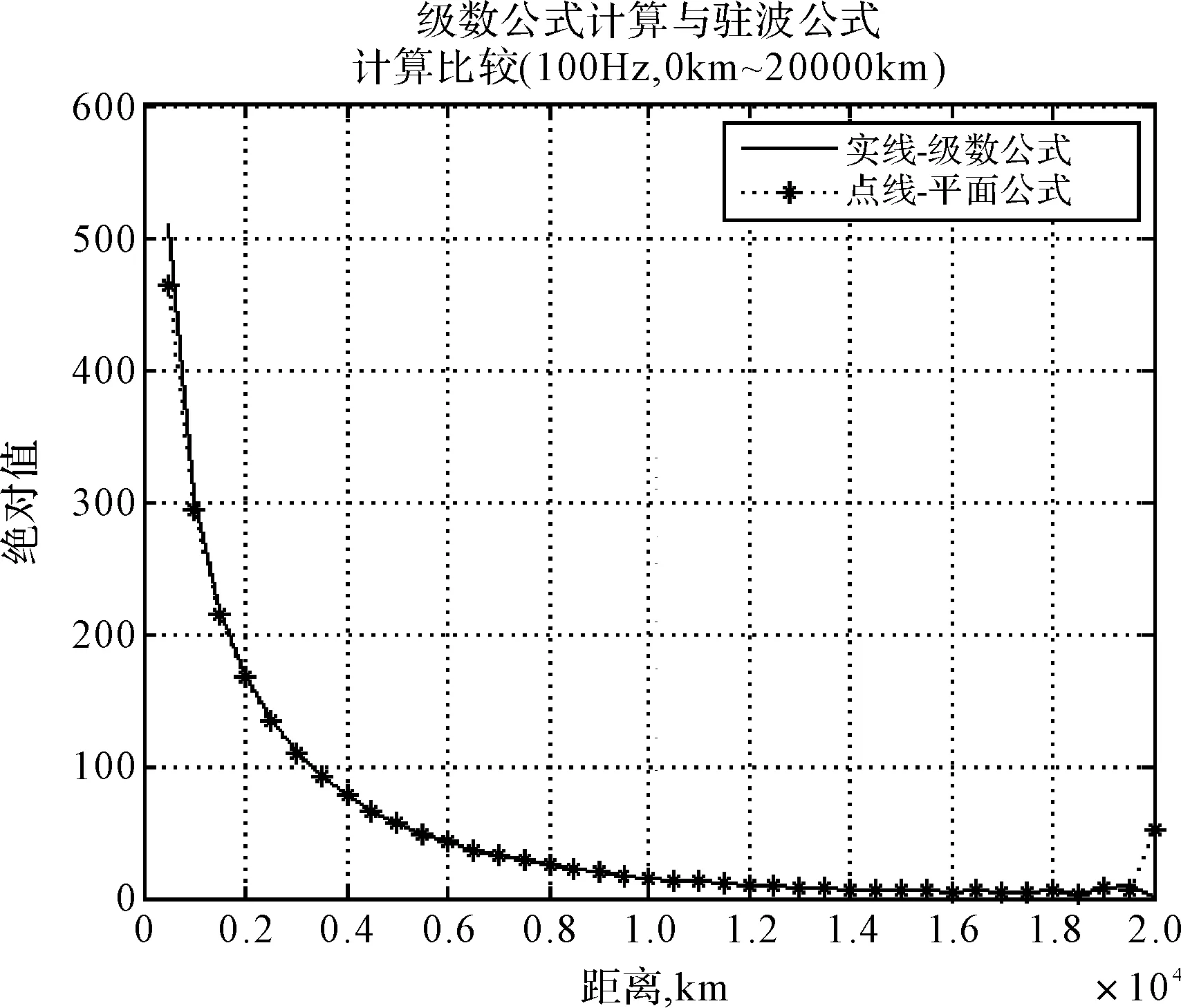
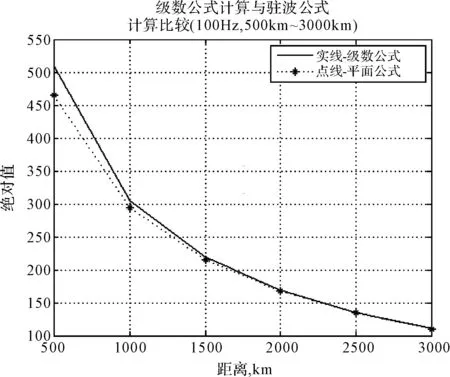
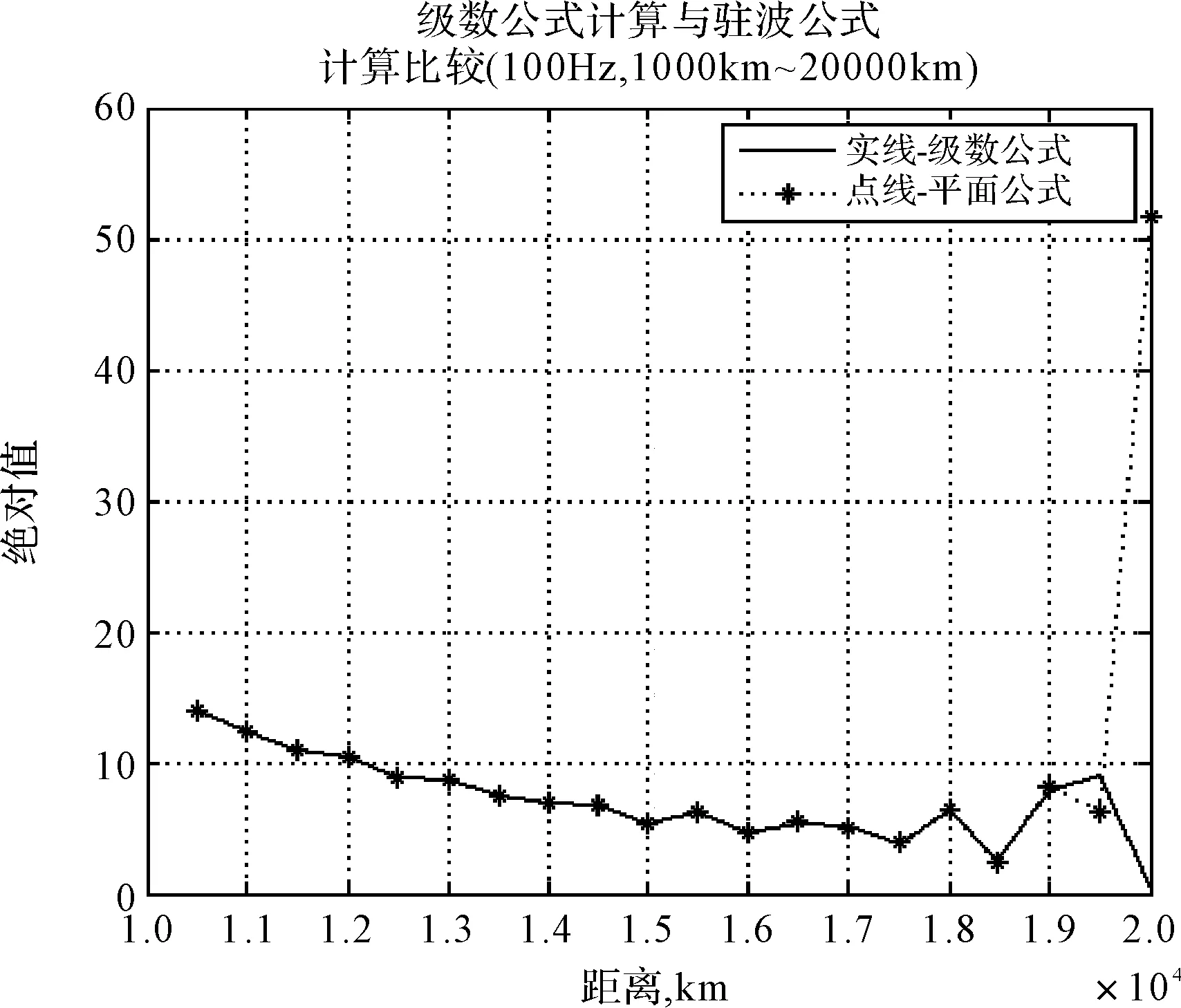
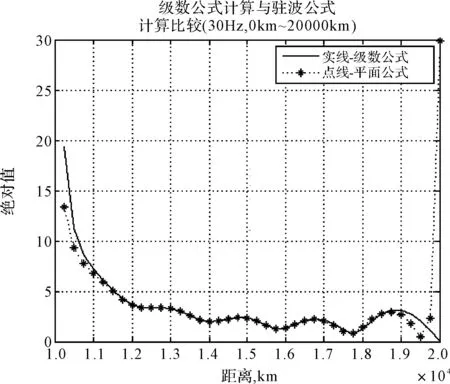
图5 勒让德函数对距离一阶导数级数表达式和驻波波导表达式对比分析

5 结语

通过对无穷级数公式和常见的三个近似公式进行编程计算,仿真分析相互比较,如果所用计算机是浮点16位尾数的,可以到到如下结论:

1) 一阶导数的级数公式理论严密、精度高,是超低频以下频率电磁场计算的首选公式。该公式可以从200km～300km至对极点的距离范围内应用,适用的频率范围大致在150Hz以下。

2) 当工作频率超过150Hz,可以应用平面近似公式,但只适用于300km以外的距离,不能用于对极点附近的电磁场,其最远适用距离大致达15000km,而且这个距离范围随频率升高而增加,适合于较高频率。

3) 当工作频率超过150Hz,距离大致从1500km至对极点的范围内,可用以对极点为中心的公式,而且随频率的增高符合的近距离更缩短,符合的程度更接近,可用于计算对极点附近的电磁场。

4) 当工作频率超过150Hz,距离大致从2000km开始至19000km范围内,可以用驻波公式。

[1] 袁翊.超低频和极低频电磁波的传播及噪声[M].北京:国防工业出版社,2011. YUAN Yi. Propagation and Noise of SLF and ELF Electromagnetic Waves[M]. Beijing: National Defense Industry Press,2011.

[2] Casey J P. Extremely Low Frequency (ELF) Propagation Formulas for Dipole Souces Radiating in a Spherical Earth-Ionosphere Waveguide[J]. NUWC-NPT Technical Report,2002(5):732-737.

[3] King W P, Margaret O, Wu T T. Lateral Electromagnetic Waves[M]. Berlin: Springer-verlag press,1992.

[4] 《数学手册》编写组.数学手册[M].北京:人民教育出版社,1979. 《Mathematics Handbook》Editorial committee. Mathematics Handbook[M]. Beijing: People’s Education Publishing Press,1979.

[5] 奚定平.贝塞尔函数[M].北京:高等教育出版社,1998. XI Dingping. Bessel Funtion[M]. Beijing: Higher Education Press,1998.

[6] Bakewell. Turbulent Wall-Pressure Fluctuations on a Body of Revolution[J]. The Journal of Acoustical Society of America,1968,43:1358-1363.

[7] Burrows M L. Motion-induced noise in electrode-palrextremely low frequency[J]. IEEE Trans. Com.,1974,22(4):540-542.

[8] 刘翠海,温东,姜波,等.无线电通信系统仿真及军事应用[M].北京:国防工业出版社,2013. LIU Cuihai, WEN Dong, JIANG Bo, et al. Radio Communication System Simulation and Military Applications[M]. Beijing: National Defense Industry Press,2013.

[9] Bannister P R. Simplified formulas for ELF propagation at shorter distances[J]. Radio Science,1986,21(3):529-537.

[10] Greifinger C, Greifinger P. On the ionospheric parameters which govern high-latitude ELF propagation in the earth- ionosphere waveguide[J]. Radio Science,1979,14(5):845-889.

Comparative Analysis of Ultra-low Frequency Atmospheric Field Legendre Function Derivative Expressions

GAI Mingming1WEN Dong1XI Hailong2CHU Juan1

(1. Navy Submarine Academy, Qingdao 266199)(2. The Navy North Sea Fleet General Staff, Qingdao 266000)

Ultra-low frequency communication atmosphere field strength calculation includes the first kind of Legendre function to the first derivative of the distance or contains the second derivative, the two derivative can be expressed as an infinite series, but infinite series calculation is under the control of the digits limit of the computer, so series computing can’t be used in high-end of ultra-low frequency. In addition, there are several approximation formula. But the approximate formula of applicable range and precision are unclear. So infinite series formulas and the approximate formula of three common are programmed and calculated by soft ware based on Matlab, comparing each other, the applicable condition and precision difference formula is determined.

ultra-low frequency, atmospheric field strength, Legendre function to the first derivative of the distance, Legendre function to the second derivative of the distance

2016年9月11日,

2016年10月23日

盖明明,女,硕士研究生,工程师,研究方向:潜艇通信。温东,男,博士,副教授,研究方向:潜艇通信。郗海龙,男,硕士研究生,工程师,研究方向:军事信息学。楚涓,女,硕士研究生,讲师,研究方向:潜艇通信。

E962

10.3969/j.issn.1672-9722.2017.03.005