基于概率迭代最近点的点云配准算法*

赵夫群 周明全 王 静

(1.咸阳师范学院教育科学学院 咸阳 712000)(2.西北大学信息科学与技术学院 西安 710127)

基于概率迭代最近点的点云配准算法*

赵夫群1,2周明全1,2王 静1

(1.咸阳师范学院教育科学学院 咸阳 712000)(2.西北大学信息科学与技术学院 西安 710127)

针对迭代最近点(Iterative Closest Point,ICP)算法中由噪声带来的配准效果不佳或失败的问题,论文提出了一种有效的含噪声点云的配准算法,即概率迭代最近点算法(Probability Iterative Closest Point,PICP)。首先,建立两个点云之间的一一对应关系,以提高算法的配准精度;然后,采用高斯概率模型解决刚体变换的问题,由此实现两个含噪声点云的精确配准。实验结果表明,该算法不仅能够快速准确地实现同一物体不同角度的带有噪声点云的配准,还能准确有效地实现刚体碎块间的断裂面的完全匹配和部分匹配问题,是一种准确、快速的配准,并能有效避免噪声和外点的干扰,适用范围更加广泛。

点云配准; 迭代最近点; 高斯模型; 概率; 噪声

Class Number TP391.4

1 引言

图像配准也叫图像匹配或图像对齐,是图像处理的一项重要技术,是图像拼接或融合的前提[1～2]。配准(registration)是指将不同成像手段所获得的同一图像的地理坐标进行匹配的过程,按照匹配的维度,主要分为二维配准和三维配准两种类型。点云配准就是一种常用的三维配准技术,是指通过固定一组点云数据的位置将另外一组点云数据向其做刚体变换的过程。目前,点云配准已经在碎片拼接[3]、图像裁切[4～5]、目标识别[6～7]以及颅面复原[8]等方面得到了广泛的应用。

在点云配准算法中,应用最为广泛的是由Besl等[9]提出的迭代最近点(Iterative Closest Point,ICP)算法,该算法步骤简单且易于实现,但是要求两个待匹配的初始点集之间存在着包含的关系,并且要求两个待配准点集的初始位置与真实位置比较接近,若不满足该条件,将会影响ICP的收敛结果甚至产生错误的匹配。针对以上问题,国内外研究者提出了很多改进的ICP算法[10～13]。Jianda Han等[14]提出了一种加强的ICP算法实现了三维环境模的快速和精确配准。Chunjia Zhang等[15]提出了一种基于有界旋转角的点云配准算法,解决了因旋转角度变化而引起的配准精度不高的问题。这些算法在一定程度上提高了配准的精度、速度或鲁棒性,但是对于存在噪声的点云数据,其配准效果不佳。2016年,Pavlos Mavridis等[16]通过结合模拟退火搜索算法和稀疏ICP算法来提高配准算法的性能,在抗噪性方面取得了一定的改进效果。Shaoyi Du等[17]提出了一种概率迭代最近点算法,克服了ICP算法中由噪声带来的配准失败问题,在一定程度上解决了m维的含噪声点云的精确配准问题。

本文针对带有噪声的点云数据,提出了一种基于概率迭代最近点(Probability Iterative Closest Point,PICP)的点云配准算法。该算法以基本ICP算法为研究基础,首先建立两个点云之间的一一对应关系,这样不仅可以抑制不重要的点,而且还能保持点对的原始信息不被噪声干扰,达到较高的配准精度。然后,本文又将高斯概率模型引入ICP算法中,采用高斯概率模型的方差由大到小逐步更新的方法,使得点云配准能够由粗到细地进行,这样既实现了粗配准,又实现了细配准,大大提高了带有噪声的点云的配准速度和精度。

2 基本ICP算法

(1)

其中,R为旋转矩阵,t为平移矩阵。

ICP算法在每次迭代过程中,都要在Y中通过寻找距离X最近的点来建立相关性,并实现刚体变换。ICP算法的基本步骤描述如下:

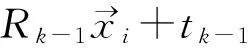
(2)

Step2:计算X和Y的刚体变换,其数学描述如下:

(Rk,tk)=

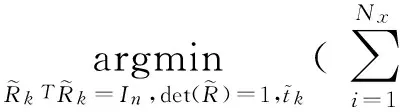
(3)

重复步骤Step1和Step2直到达到迭代终止条件为止。由于ICP算法是一个局部收敛算法,因此旋转矩阵和平移矩阵的初值非常重要。好的初值不仅保证算法能收敛到全局最小值,而且能大大提高算法的执行效率。初值的选取可参考文献[18～19]的选取方法。

3 PICP算法

PICP算法是在基本ICP算法的基础上引入高斯概率模型来实现的。点集X和Y之间的概率是在每次迭代过程中实时计算得到的。整体来说,因为噪声点的距离较远,所以高斯模型计算的概率较小。因此用PICP算法进行配准时,噪声点对配准结果的影响并不大。那么,两个带有噪声的点集X和Y之间的配准就可以转化成概率密度估计的问题。根据全概率定理,点集X的概率公式可表示为

(4)

若点集X和Y都满足高斯概率模型,那么它们之间的关系可描述为

(5)

这里为了简化模型,假设模型点集Y服从均匀分布,即

(6)

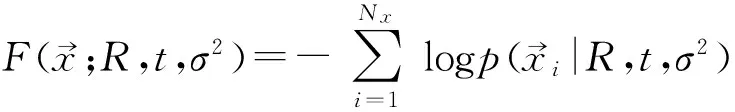
(7)

PICP算法分为两个主要实现步骤:

1) 根据第k-1步的刚体变换Rk-1和tk-1,建立点集X和Y的相关性,其数学描述如下:

(8)

该步骤建立了点集X和Y之间的一对一相关性。由于这个过程抑制了不重要的点并保持了点对的原始信息不受噪声的干扰,因此可以大大减少计算时间并在一定程度上提高配准精度。

2) 基于第1)步求解新的刚体变换,并用奇异值分解(Singular Value Decomposition,SVD)方法来计算相关点的概率,再根据两个点集之间的距离和方差就计算出后验高斯概率。这里,由于高斯概率模型的方差是从大到小逐步变化的,这就使得配准过程是从粗到细的,避免算法陷入局部最小值。

首先,建立新的目标函数如下

(9)

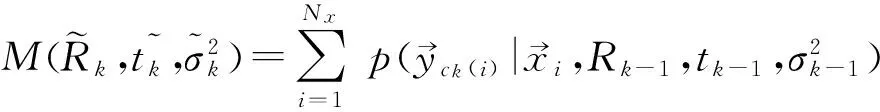
(10)

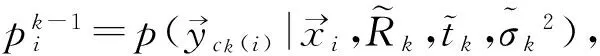
(11)

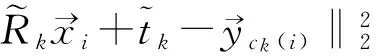
(12)

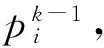
(13)

方差可以表示为

(14)

那么,高斯概率方差的更新公式为

(15)

其中,λ称作退火系数。当λ=1时,方差不会更新,就是所谓的ICP算法。当λ取值较大时,就可以有效地提高迭代速度,但是容易陷入局部最小值。因此一般λ的取值在1～2之间,具体取值由实验来决定。

因此,后验高斯概率的计算公式为

(16)

重复执行1)和2)两个步骤就实现了PICP算法的两个点集的配准问题。PICP算法的终止条件为:在每次迭代结束时,都判断算法是否达到终止条件,若相邻两次迭代的RMS的差值|RMSk-RMSk-1|小于给定阈值ε或达到最大迭代次数Stepmax,算法就停止迭代,此时算法取得了最优最小值,从而实现了两个点集的配准。

下面给出PICP算法的具体实现步骤:

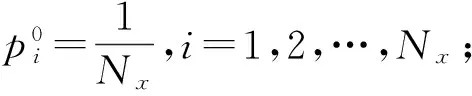
Step2:令X=R0X+t0,迭代次数k=0;

Step3:令k=k+1,利用式(8)建立相关性ck(i),i=1,2,…,Nx;

Step4:利用式(12)的SVD方法计算旋转矩阵Rk和平移矢量tk;

Step5:利用式(14)计算两组点集的方差;

Step6:利用式(15)更新高斯概率的方差;

Step7:利用式(16)计算后验高斯概率直到满足|RMSk-RMSk-1|<ε或k>Stepmax。

4 实验结果与分析

本文的实验数据源于Stanford 3D Scanning Repository[20],采用了两组带有噪声的点云数据进行配准实验,分别如图1和图2所示。图1是第一组点云数据,采用了bun000和bun045两个点云数据,分别如图1(a)和图1(b)所示,图1(c)是点云bun000和bun045的初始相对位置。图2是第二组点云数据,采用了dragonStandRight_0和dragonStandRight_24两个点云数据,分别如图2(a)和图2(b)所示,图2(c)是点云bun000和bun045的初始相对位置。

实验中,分别采用ICP算法和PICP算法对第一组点云数据和第二组点云数据进行配准,其配准结果分别如图3和图4所示。图3是第一组点云数据的配准结果,图3(a)是ICP算法的配准结果,图3(b)是PICP算法的配准结果。图4是第二组点云数据的配准结果,图4(a)是ICP算法的配准结果,图4(b)是PICP算法的配准结果。从图3和图4的配准结果来看,PICP算法较ICP算法的配准结果更好,得到了更多的配准点对,配准的精度更高,误差更小。其具体的配准点数、RMS、迭代次数和耗时等配准结果参数如表1所示。

图1 第一组待配准的两个点云

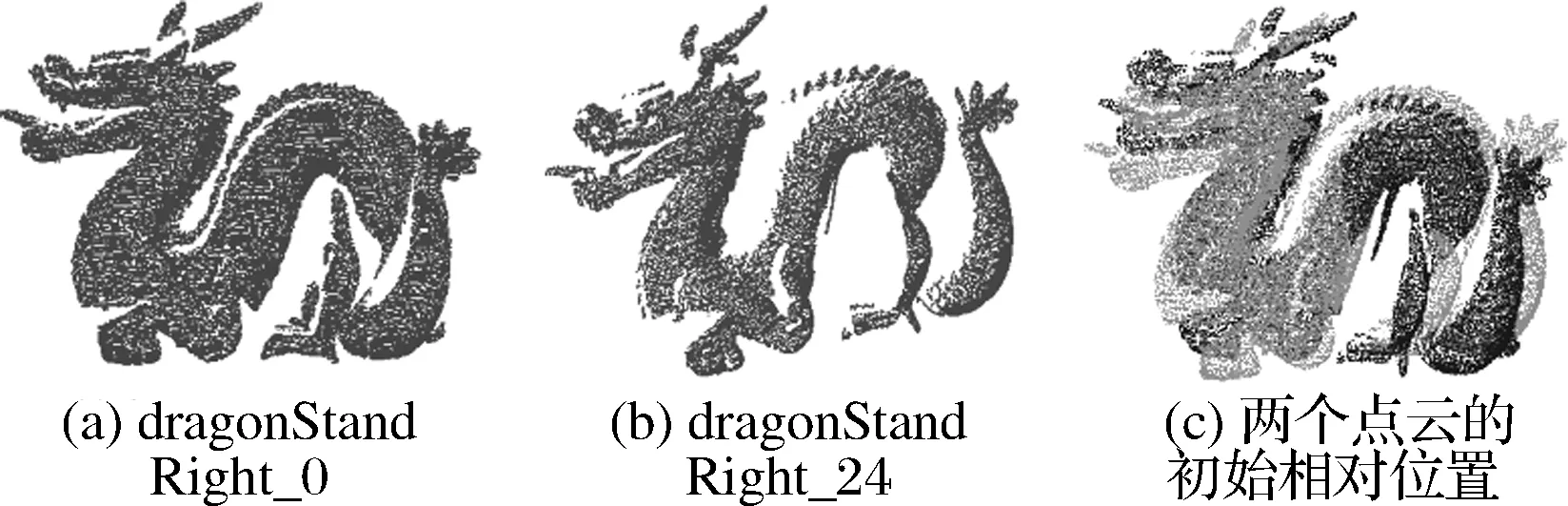
图2 第二组待配准的两个点云

图3 第一组点云的配准结果

图4 第二组点云的配准结果

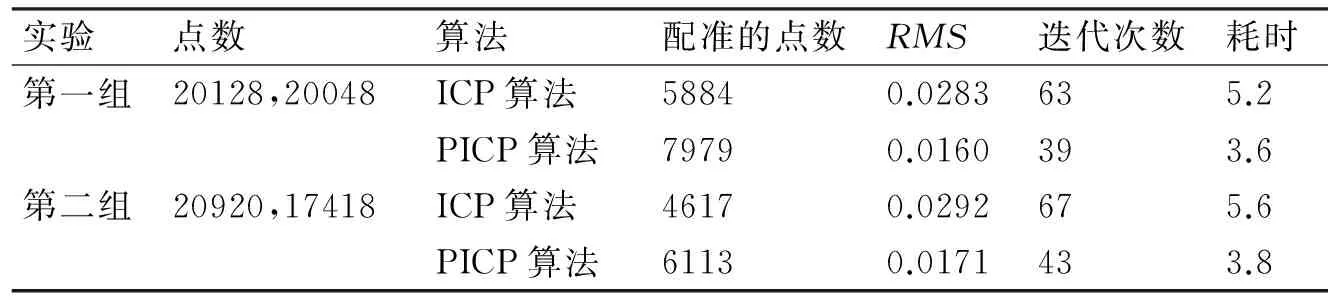
表1 两组点云的配准结果参数(时间单位:s)

从表1可见,对于第一组点云,与ICP算法相比,PICP算法的配准点数提高了35.6%,RMS降低了43.5%,迭代次数降低了38.1%,耗时降低了30.8%。对于第2组点云,与ICP算法相比,PICP算法的配准点数提高了32.4%,RMS降低了41.4%,迭代次数降低了35.8%,耗时降低了32.1%。由此可见,PICP算法的配准效果要远优于ICP算法的配准效果,该算法大大提高了带有噪声的点云的配准个数,降低了RMS、迭代次数和耗时,并具有较强的鲁棒性。因此说,PICP算法是一种快速、精确的点云配准算法,并且配准结果不受噪声的干扰。

5 结语

点云配准技术研究已久,各种配准算法都是围绕着配准的精度、速度以及鲁棒性等方面展开的,本文主要针对带噪声点云的配准问题,提出了一种基于概率迭代最近点的点云配准算法。该算法不仅通过建立两个点云之间的点的一一对应关系在一定程度上排除了不重要的点和噪声点,大大提高了点云配准的精度,而且还通过引入高斯模型的方式,通过求解其概率模型的距离和方差实现了点云由粗到细的配准,进一步提高了配准的精度。该算法不仅是对ICP算法在配准精度、速度等方面的一个改进,更是一种针对噪声点云的有效配准算法。在今后的研究中,会将该算法引入到更加复杂刚体碎块的复原研究中,如含有大量噪声的复杂秦俑碎块的虚拟拼接复原,以进一步提高碎块匹配的精度、速度、鲁棒性和抗噪性。

[1] 龚伦,刘璨,胡均谱.一种改进Harris角点与SIFT的图像拼接技术[J].计算机与数字工程,2015,43(11):2055-2060. GONG Lun, LIU CAN, HU Junpu. A New Image Stitching Technology Based on Harris Corner and SIFT[J]. Computer & Digital Engineering,2015,43(11):2055-2060.

[2] 孙晓宁,陆文骏.一种新的雾天图像显著性检测方法[J].计算机与数字工程,2015,43(11):2029-2034. SUN Xiaoning, LU Wenjun. A New method of Salient Object Detection in Foggy Images[J]. Computer & Digital Engineering,2015,43(11):2029-2034.

[3] E. Altantsetseg, K. Matsuyama, K. Konno. Pairwise matching of 3D fragments using fast fourier transform[J]. Visual Computer,2014,30:929-938.

[4] L. Zhang, M. Song, Q. Zhao, et al. Probabilistic Graphlet Transfer for Photo Cropping[J]. IEEE Transactions on Image Processing,2013,22:802-815.

[5] L. Zhang, M. Song, Y. Yang, et al. Weakly Supervised Photo Cropping[J]. IEEE Transactions on Multimedia,2014,16:94-107.

[6] Y. Gao, M. Wang, D. Tao, et al. 3-D Object Retrieval and Recognition With Hypergraph Analysis[J]. IEEE Transactions on Image Processing,2012,21:4290-4303.

[7] Y. Gao, M. Wang, R. Ji, et al. 3-D Object Retrieval With Hausdorff Distance Learning[J]. IEEE Transactions on Industrial Electronics,2014,61:2088-2098.

[8] 税午阳,周明全,武仲科.数据配准的颅骨面貌复原方法[J].计算机辅助设计与图形学学报,2011,23(4):607-614. SHUI Wuyang, ZHOU Mingquan, WU Zhongke. An Approach of Craniofacial Reconstruction Based om Registration[J]. Journal of Computer-Aided Design & Computer Graphics,2011,23(4):607-614.

[9] P.J. Besl, N.D. McKay. A method for registration of 3-Dshapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1992,14:239-256.

[10] C.V. Stewart, C.-L. Tsai, B. Roysam. The dual-boot strap iterative closest point algorithm with application to retinal image registration[J]. IEEE Transactions on Medical Imaging,2003,22:1379-1394.

[11] M. Herrmann, M. Otesteanu, M. Otto. Fast and robust point cloud matching based on EM-ICP prepositioning[C]//2012 10thInternational Symposium on Electronics and Telecommunications(ISETC),2012:99-103.

[12] F. Aghili, M. Kuryllo, G. Okouneva, et al. Robust vision-based pose estimation of moving objects for Automated Rendezvousamp; Docking[C]//2010 International Conference on Mechatronics and Automation(ICMA),2010:305-311.

[13] S. Du, N. Zheng, L. Xiong, et al. Scaling iterative closest point algorithm for registration of m-D point sets[J]. Journal of Visual Communication and Image Representation,2010,21:442-452.

[14] Jianda Han, Peng Yin, Yuqing He. Enhanced ICP for the Registration of Large-Scale 3D Environment Models: An Experimental Study[J]. sensors,2016,16(228):1-15.

[15] Chunjia Zhang, Shaoyi Du, Juan Liu, et al. Robust 3D Point Set Registration Using Iterative Closest Point Algorithm with Bounded Rotation Angle[J]. Signal Processing,2016,120:777-788.

[16] Pavlos Mavridis, Anthousis Andreadis, Georgios Papaioannou. Efficient Sparse ICP[J]. Computer Aided Geometric Design,2015,35:16-26.

[17] Shaoyi Du, Juan Liu, Chunjia Zhang. Probability iterative closest point algorithm for m-D point set registration with noise[J]. Neurocomputing,2015,157:187-198.

[18] C.V. Stewart, C. Tsai, B. Roysam. The dual-boot strap iterative closest point algorithm with application to retinal image registration[J]. IEEE Trans. Med. Imaging,2003,22:1379-1394.

[19] L. Liu, X. Hu,Y. Chen, et al. A new close-form solution for initial registration of ICP. Adv. Mater. Res.,2011,143:287-292.

[20] The Stanford 3D Scanning Repository[EB/OL]. 1996. http://graphics.stanford.edu/data/3Dscanrep/.

Point Cloud Registration Algorithm Based on Probability Iterative Closest Point

ZHAO Fuqun1,2ZHOU Mingquan1,2WANG Jing1

(1. College of Education Science, Xianyang Normal University, Xianyang 712000) (2. College of Information Science and Technology, Northwest University, Xi’an 710127)

Aiming at the failure registration of iterative closest point (ICP) algorithm brought by noise, the paper proposes a point cloud registration algorithm with noise based on Expectation Maximum (EM) estimation, which is named probability iterative closest point (PICP) algorithm. Firstly, a point-to-point correspondence is built between two point clouds, thus the registration accuracy is improved greatly. Then, Gaussian model is introduced into ICP algorithm, the singular value decomposition (SVD) method is used to solve the problem of rigid body transformation, thus the accurate registration of two point clouds is completed. The experimental results show that PICP algorithm not only can complete point clouds registration with noise of the same object from different angles rapidly and accurately, but also can achieve complete matching and partial matching of fracture surfaces between rigid body blocks effectively. It is an accurate and fast algorithm which can effectively avoid noise and external interference. It has more extensive application scopes.

point cloud registration, iterative closest point, Gaussian model, probability, noise

2016年9月5日,

2016年10月13日

国家自然科学基金项目(编号:61373117)资助。

赵夫群,女,博士研究生,讲师,研究方向:图形图像处理。周明全,男,教授,博士生导师,研究方向:图形图像处理,三维重建。王静,女,硕士,研究方向:信息技术及其应用。

TP391.4

10.3969/j.issn.1672-9722.2017.03.002