基于灰色自适应等维递补算法的区域经济产值预测*

陈雪改 王 飞

(河海大学商学院 南京 211100)

基于灰色自适应等维递补算法的区域经济产值预测*

陈雪改 王 飞

(河海大学商学院 南京 211100)

针对GM(1,1)模型时间序列数据量少、数据信息不完整带来的预测误差问题,通过运用分析未知数据的预测方法以及时间序列的数据特征,在改进原始模型缺陷的基础上,提出一种新的预测方法—自适应灰色递补算法。结合预测方法的理论推导过程,总结出预测的算法步骤,使得预测计算过程更简洁。最后,利用A省的生态农业发展模式近几年经济产值的实际数据来验证预测算法,结果表明:农业观光园、民俗景区旅游和设施农业三种形式生态农业产值预测误差分别仅为0.04、0.001和0.0008,作为一种全新的方法,该算法对时间序列数据的预测具有较高的精度。

灰色系统; GM(1,1)模型; GM(1,n)模型; 数据预测; 生态农业; 经济产值

Class Number TN02

1 引言

目前,对于经济产值、年度GDP等时间序列的数据的研究已经有了相当成熟的理论成果[1]。为了节省数据的存储空间,数据库往往只存储原始数据,那么对于时间序列数据的预测就成为了一个非常重要的课题[2]。传统的回归预测、神经网络等预测模型通常对计算方法以及样本数据的容量和质量都有较高的要求[3～4]。由于现有数据收集以及存储的技术手段落后,大多数的统计数据通常会存在时间序列短、数据库数据量少、数据信息不完整等问题[5]。针对这些数据序列,灰色系统预测算法是一种比较合适的预测方法[7]。本研究在这类预测模型算法的基础上,借助变量的微分形式建立预测模型,利用时间序列数据的实时动态变化的特点改进原算法的自适应性,对数据进行循环滚动处理,从而保证数据序列的动态性,根据现有数据做出较为准确的预测数据。另外,综合分析了预测算法的具体过程并通过实例验证给出算法的有效性。

2 算法的基础思想

2.1 自适应灰色预测的基本思想

GM(1,1)灰色预测模型是灰色系统的核心理论部分,它通过已知的数据将系统信息的一些抽象概念进行量化,建立量化模型,进而进行优化模型预测未知的数据信息[8～9]。具体是将无规律的数据资料进行累加,生成具有规律性的数列,在计算机环境下实现预测算法对数据得到处理过程[10],则得到原始数据的预测值。其模型定义如下

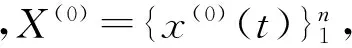
Y=(r0(i)),B=(-z1(i),1)(n-1)×2,i=1,…,n

(1)

2.2 等维灰色递补的基本思想

GM(1,1)模型由当前时刻开始来预测将来时刻,要预测的未来时刻越远,得到预测值的灰区间越大,影响长期预测的效果,只能给出大致的趋势要求[11]。这是因为预测模型算法设置灰参数值估计的时候没有考虑到它的动态时变性[12～13]。针对这个动态问题,GM(1,1)预测相关算法考虑采用已知时序数列计算得出一个预测值,随后利用算法流程中的循环节将新的预测值添加到已知时序数列,来替代序列中最老的那一项数据,确保序列维数不变,这样就能够使预测灰数不断地进行新陈代谢,依次迭代预测,逐个进行递补,循环进行就能够完成预测目标,其核心是递补预测数据确保时序数列保持维数相等。

3 自适应灰色递补算法

3.1 预测模型的建立

考虑到模型的适用性,首先将GM(1,1)预测模型拓展到包含多个变量的GM(1,n)预测模型[14],结合变量间的相互关系,将模型继续改进得到MGM(1,n)模型即自适应灰色递补预测模型。

对于时间序列变量对应的1-GAO序列,其MGM(1,n)的预测模型为

X(1)(t)=eAtX(1)(0)+A-1(eAt-I)

(2)

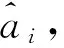
这样就可以得到修正后的MGM(1,n)预测模型:

(3)

3.2 模型预测的算法步骤

根据对灰色等维递补算法的分析,可以其具体算法描述如下

Step2:利用迭代计算公式X(1)(t)=eAtX(1)(0)+A-1(eAt-I)对X(1)(k)进行相应的处理,即计算预测变量的连续时间序列;

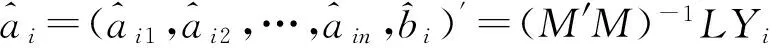
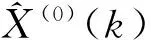
以上算法步骤所对应的流程图如图1所示。

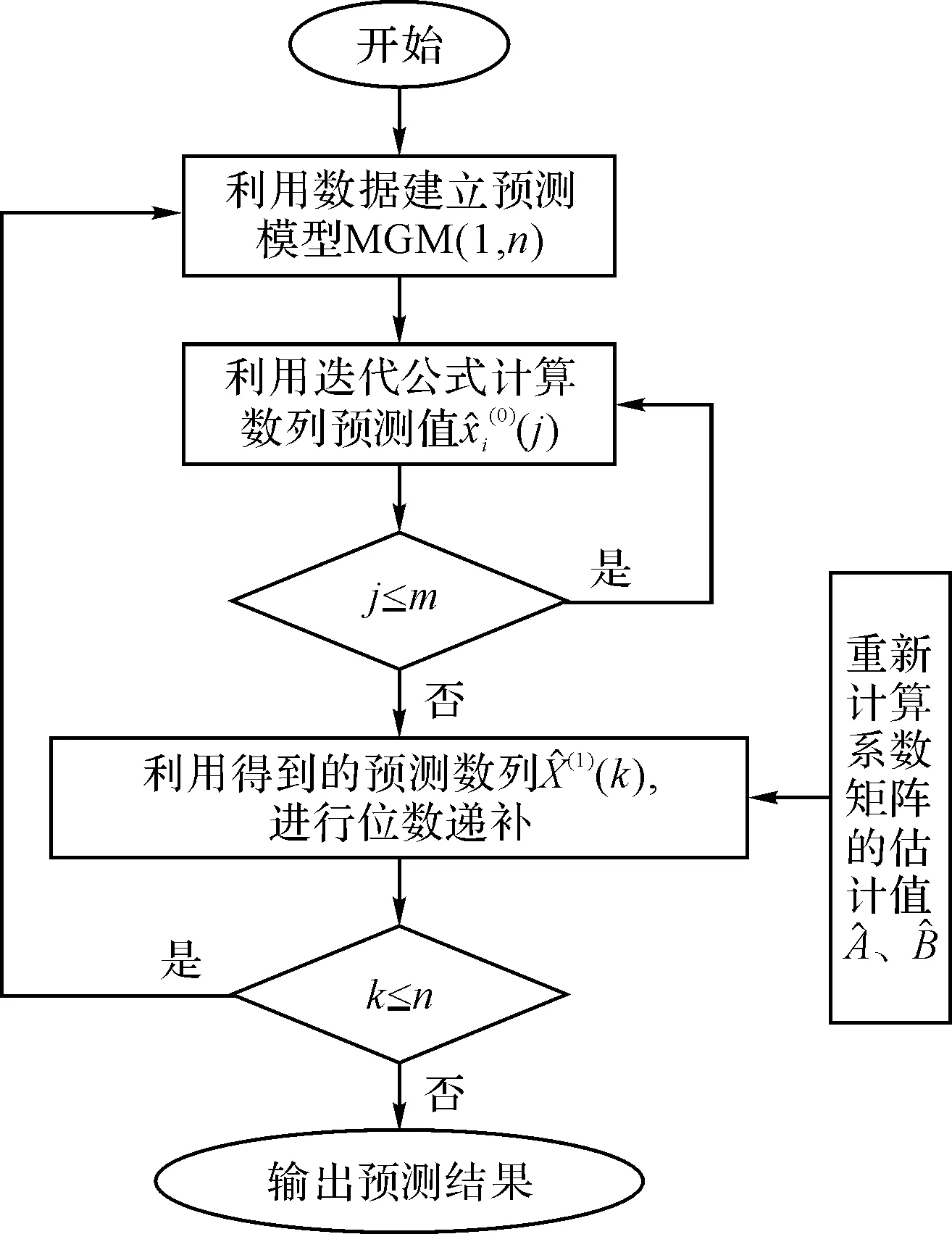
图1 自适应灰色等维递补算法的流程图

4 实例验证

A省该地区生态农业的主要表现形式有三种:农业观光园Y1、民俗景区旅游Y2、设施农业Y3,并将以上三个变量的产值以及三者的产值之和Y0作为系统特征变量。另外,分别用X1、X2、X3、X4表示生态产业产值、农林牧总产值、农林牧业方向上的技术合同成交项数量和农村固定资产投资额度这四种影响生态农业发展的因素,并采用改进的MGM(1,n)模型对三种生态农业形式未来五年产值变化进行预测比较,分析该省五年内生态农业的发展方向。其原始数据如表1所示。

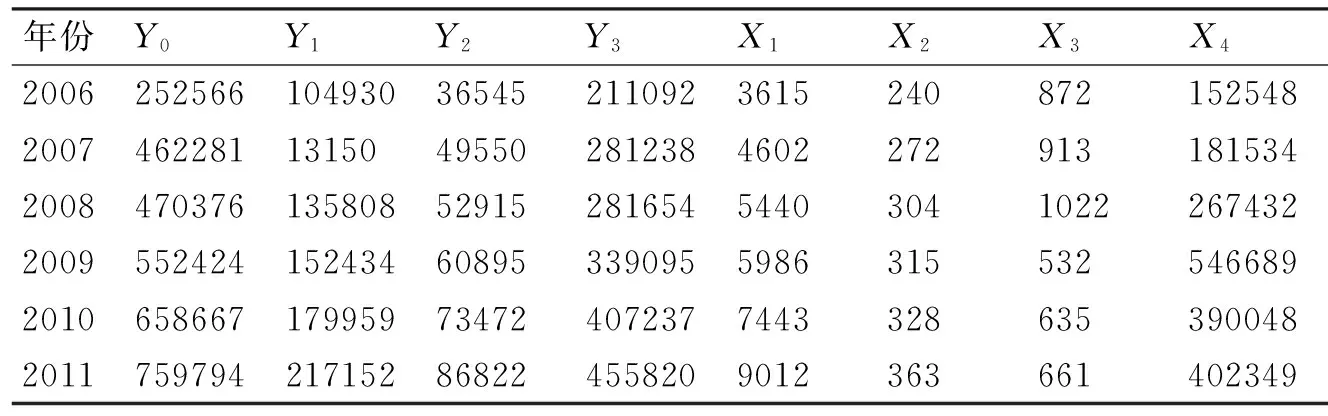
表1 A省生态农业及相关因素原始数据表(单位:万元项)

现在就利用上一部分改进的MGM(1,n)模型预测未来五年三种形式生态农业的产值变化,分析A省生态农业未来五年内农业发展的方向。另外从生态农业消费市场容量以及发展投资角度,考虑上述三种形式生态农业之间的相互影响、相互联系,运用改进的自适应灰色递补预测模型对其收入进行预测。模型包含的相关因素不仅包含Xi,i=1,…,4,而且也包含系统变量Yi,i=1,…,3,因此MGM(1,n)预测模型中n=6。这样采用该模型对三种不同形式生态农业五年(2011～2015)产值变化进行预测,结果如表2所示。

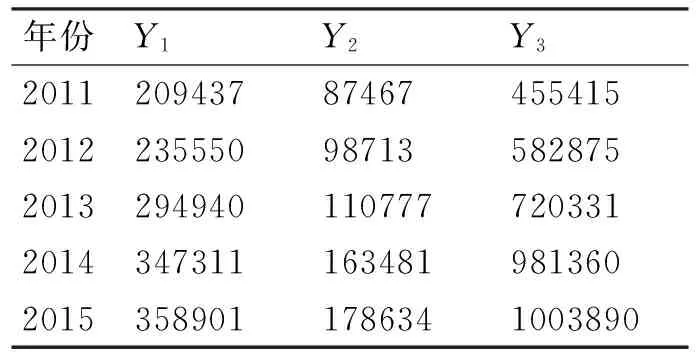
表2 2011～2015年不同形式生态农业产值预测值

另外,为了表现农业观光园、民俗景区旅游、设施农业三个系统变量的产值变化趋势,绘制三个变量2006～2015年的产值以及预测值折线图如图2所示。

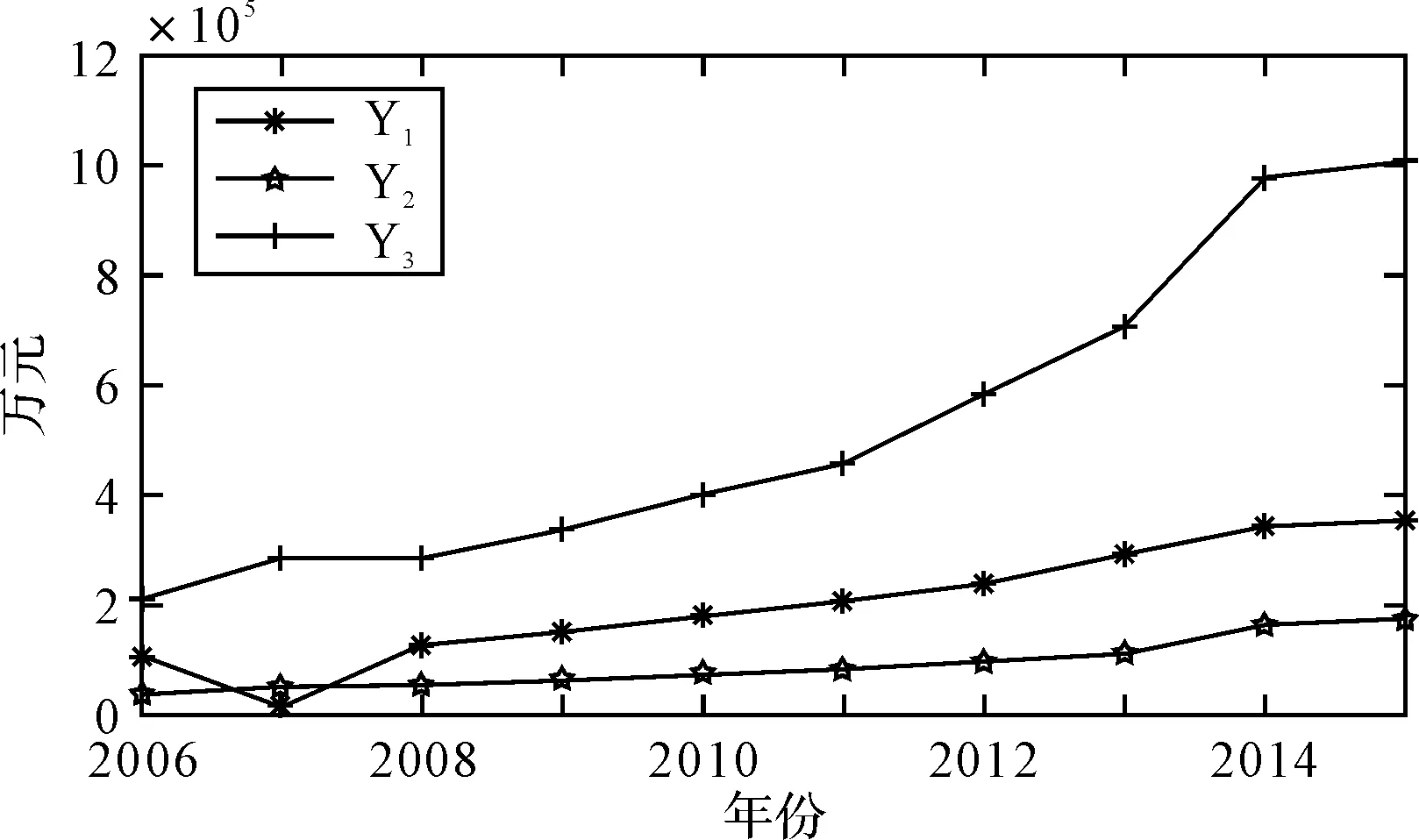
图2 2006～2015年三个变量的产值以及预测值折线图

为了能够直观地看出预测结果的效果,下面运用残差检验对序列Y1、Y2、Y3、X1、X2、X3、X4的预测值与实际值的误差进行检验,结果如表3所示。

表3 不同系统变量残差检验平均相对误差(单位:%)

由残差检验平均相对误差可知基于自适应MGM(1,n)模型的预测算法对不同系统变量Yi,i=1,…,3及其他四个序列Xi,i=1,…,4都具有较高的拟合精度。另外,将表2中三种形式生态农业产值的2011年预测值与表1中三者产值的原始数据对比,得到误差水平分别为0.04、0.001、0.0008,远小于临界值0.05的水平,因此采用自适应MGM(1,n)预测模型对于这三种不同形式生态农业发展速度的预测具有较高的精度。

5 结语

通过多变量的自适应灰色等维预测算法对A省生态农业2011～2015年生态农业发展方向预测的结果,可以看出,未来五年内(2011～2015年)该省生态农业中的农业观光园、民俗旅游、设施农业产值都将不断增长。因此从农林牧发展速度和农村投资结构的角度来看设施农业和农业观光园产值占生态农业总产值的比重将不断提高,因此在全面发展生态农业的同时,二者将优先发展。

根据预测算法的计算过程以及对预测结果的验证,不仅仅说明了预测模型以及算法的正确性,更重要的是本文提出的预测方法提供了对时间序列的未来一段时期内数据预测的一种全新的方法。

[1] 杨得志.广义回归神经网络在乙肝发病数时间序列预测中的应[J].计算机应用与软件,2013,30(4):217-220. YANG Dezhi. Application of General Regression Neural Network in Hepatitis B Incident Cases Time Series Forecasting[J]. Computer Applications and Software,2013,30(4):217-220.

[2] 吴江,孙剑伟.一种基于云模型的数据预测算法[J].软件,2015,36(12):211-215. WU Jiang, SUN Jianwei. An Algorithm of Data Prediction Based On Cloud Model[J]. Computer Engineering & Software,2015,36(12):211-215.

[3] 谢华为.基于灰色系统理论的道路交通事故预测[J].交通与运输(学术版),2015(2):56-59. XIE Huawei. Prediction of road traffic accidents based on grey system theory and grey system theory[J]. Transportation and transportation(Academic),2015(2):56-59.

[4] 韩亚坤,周吕,陈冠宇,等.灰色GM(1,1)与Kalman滤波模型用于变形预测的比较分析[J].测绘工程,2015(2):12-15. HAN Yankun, ZHOU Lv, CHEN Guanyu, et al. Comparison and analysis of grey GM(1,1) and Kalman filtering model for prediction of deformation[J]. Geospatial Information,2015(2):12-15.

[5] 卓广平.高效数据挖掘算法在大规模数据集中的应用研究[J].软件,2014,35(8):72-74. ZHUO Guangping. Applied Research on Large-scale Date Sets for Efficient Data Mining[J]. Computer Engineering & Software,2014,35(8):72-74.

[6] 孟小峰,慈祥.大数据管理:概念、技术与挑战[J].计算机研究与发展,2013,50(1):146-169. MENG Xiaofeng, CI Xiang. Big Data Management: Concepts, Techniques and Challenges[J]. Journal of Computer Research and Development,2013,50(1):146-169.

[7] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2010:55-101. LIU Sifeng, DANG Yaoguo, FANG Zhigeng. Grey System Theory and Its Application[M]. Beijing: Science Press,2010:55-101.

[8] 谢明柱,查奇芬.基于GM(1,1)改进模型的我国农村人口老龄化预测[J].长江论坛,2013(4):42-45. XIE Mingzhu, CHA Qifen. The Prediction of China’s Rural Population Aging Based on GM(1,1) Improved Model[J]. Yangtze Tribune,2013(4):42-45.

[9] 程丽萍.灰色优化GM(1,1)和人工神经网络组合模型的江西省GDP预测应用[J].萍乡高等专科学校学报,2012(3):47-49. CHENG Liping. Grey Optimized GM(1,1) and Artificial Neural Network Combined Model of Jiangxi Province GDP Forecast Application[J]. Journal of Pingxiang College,2012(3):47-49.

[10] 师金钢,鲍玉斌,冷芳玲.基于MapReduce的关系型数据仓库并行查询[J].东北大学学报(自然科学版),2011,5(5):626-629. SHI Jingang, BAO Yubin, LENG Fangling. Parallel Query for a Data Warehouse Utilizing MapReduce[J]. Journal of Northeastern University(Natural Science),2011,5(5):626-629.

[11] 郭常莲,强彦,孙然.灰色系统理论预测算法研究及其在农村经济分析中的应用[J].电脑的开发与应用,2011,24(4):7-10. GUO Changlian, QIANG Yan, SUN Ran. On the Grey Prediction Algorithm and Its Application to the Rural Economy Analysis[J]. Compuer Development & Applications,2011,24(4):7-10.

[12] 牛移民.桥梁施工监控与灰色系统理论的应用[J].交通世界:运输车辆,2015(36):86-87. NIU Yimin. Bridge Construction Monitoring and Application of Grey System Theory[J]. Transpo World,2015(36):86-87.

[13] 刘笑冰,陈建成,何忠伟.基于MGM(1,N)模型的北京创意农业发展灰色预测[J].中国人口·资源与环境,2013,23(4):62-67. LIU Xiaobing, CHEN Jiancheng, HE Zhongwei. Grey Forecasting Analysis on Creative Agricultural Development in Beijing Based on MGM(1,N) Model[J]. China Population Resources and Environment,2013,23(4):62-67.

[14] 张胜跃,卿黎,张宇栋.基于雨流-灰色GM(1,1)模型的锅炉焊接头疲劳寿命预测[J].中国安全科学学报,2015,25(12):62-68. ZHANG Shengyue, QIN LI, ZHANG Yudong. Fatigue Life Prediction of Boiler Welded Joint Based on Rain Flow-Grey GM(1,1) Mode[J]. China Safety Science Journal,2015,25(12):62-68.

[15] 邓朝晖,刘洋,薛惠锋.基于VAR模型的水资源利用与经济增长动态关系研究[J].中国人口:资源与环境,2012(6):68-70. DENG Zhaohui, LIU Yang, XUE Huifeng. Study on the Dynamic Relationship Between Economic Growth and Water Resources-Use Based on the VAR Model[J]. China Popuation Resources and Environment,2012(6):68-70.

[16] 栾文鹏,余贻鑫,王兵.AMI数据分析方法[J].中国机电工程学报,2015,35(1):29-37. LUAN Wenpeng, YU Yixin, WANG Bing. AMI Data Analytics[J]. Proceedings of the CSEE,2015,35(1):29-37.

Area Economic Output Forecast Based on Gray Recurrence Equal Dimension Algorithm

CHEN Xuegai WANG Fei

(School of Business, Hohai University, Nanjing 211100)

The GM(1,1) model has a prediction error problem caused by less time-series data, incomplete data, by analyzing prediction methods of unknown data and features of time series data, on the basis of improving the original model defect, a new prediction method-adaptive algorithm gray fill vacancies is proposed. Combined with prediction theory derivation process, prediction algorithm steps are summarized to make prediction calculation process more concise. Finally, economic output of province A ecological agriculture development model of in recent years is used to to verify the prediction algorithm, the results show that agricultural sightseeing garden, folk scenic tourist facilities and three forms of ecological agriculture agricultural output prediction error are only 0.04, 0.001 and 0.0008, As a new method, the algorithm to predict the time series data has high accuracy.

grey system, GM(1,1) model, GM(1,n) model, data forecast, ecological agriculture, economic output

2016年9月11日,

2016年10月17日

国家社会科学规划基金资助一般项目(编号:15BGL054);江苏高校哲学社会科学研究重点项目(编号:20162DIXM008);自然科学基金项目(编号:71603070)资助。

陈雪改,女,硕士研究生,研究方向:公司金融。王飞,男,硕士生导师,研究方向:财务管理和会计金融。

TN02

10.3969/j.issn.1672-9722.2017.03.001