光电系统光轴与机械轴同轴度测试方法
2017-03-30高洋洋景文博尹超平王晓曼张汝平
高洋洋,景文博,尹超平,王晓曼,张汝平
(1.长春理工大学电子信息工程学院,长春 130022;2.长春理工大学光电工程学院,长春 130022;3.大陆汽车电子(连云港)有限公司,长春 130000)
光电系统光轴与机械轴同轴度测试方法
高洋洋1,景文博2,尹超平3,王晓曼1,张汝平1
(1.长春理工大学电子信息工程学院,长春 130022;2.长春理工大学光电工程学院,长春 130022;3.大陆汽车电子(连云港)有限公司,长春 130000)
同轴度是光学系统的重要技术指标。目前比较先进的方法是利用激光准直方法测量同轴度,但其仅仅认为同轴度属于二维的范畴,忽略了其三维空间性,即在三维空间里水平与俯仰方向同轴度之间的相互影响。因此,提出一种基于三维空间建模的方法,对同轴度进行测试。首先,建立机械轴与光轴的空间关系模型;其次,定位光斑质心;再次,对获得的光斑图像坐标,进行圆轨迹拟合;最后,将光斑圆轨迹上的任一点坐标代入到光轴与机械轴的旋转模型,即可获得二者的同轴度。实验结果表明:俯仰偏转角度对水平偏转角度的影响不可忽略,该方法使水平方向的同轴度测量精度得到显著提高。此方法对于同轴度的评估具有十分重要的应用价值。
同轴度;高分辨率CCD;光斑质心亚像素定位;旋转矩阵
炮口轴线的偏差是影响坦克射击精度的重要因素之一,这就要求标校火炮炮口线的光电系统有非常出色的质量,即高标准的精度。但是在集成组装光电系统的时候难免会使电子校炮镜的光轴与外部套筒的机械轴发生偏离,所以对电子校炮镜的同轴度的精确检测是保证该光电系统精度的关键。
同轴度的测量方法有很多,主要包括目视瞄准靶板法、平行光管法[1]、火炮瞄准激光光电靶法、基于图像处理的投影靶板法等[2],大多是利用光学方法、机械方法,或者是两者相结合的方法,不但过程复杂,而且使用的仪器和设备也不是十分先进,基本都需要人工判读或者人工目视瞄准,这其中掺杂着大量的人为干扰因素,测量精度不是很高[3]。本文采用的图像处理技术和机器视觉相结合的检测模式,弥补了人眼识别率有限和不稳定的不足,并且把思考方式从二维平面提升到了三维空间,从三维空间关联性入手,充分地考虑了造成同轴度误差的角度影响因素,有效地保证了测量精度。
1 同轴度测量系统工作原理
图1为光电系统同轴度测量示意图。同轴度是指校炮镜光轴对火炮机械轴的变动量,如果该变动量的值为零,则代表这两条轴线同轴,即利用标准炮口来测试光电系统的同轴度。首先,使平行光光管发出的平行光光轴与标准炮口的机械轴重合;其次,将校炮镜放到标准炮口里面,光斑成像在上位机显示界面上;最后,对采集到的光斑位置与成像界面的中心位置进行比较,若校炮镜光轴与标准炮口的机械轴重合,则光斑显示成像界面的中心位置,代表二者同轴,否则,成像在除中心以外其他的位置,代表二者不同轴。
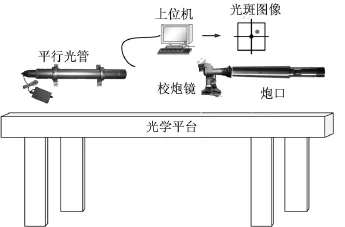
图1 光电系统同轴度测量系统工作原理图
根据CCD成像原理建立空间坐标系,如图2所示。以镜头处为坐标原点,镜头焦距为f,空间直角坐标系OXYZ的Z轴与机械轴重合,空间直角坐标系OX'Y'Z'的Z'轴与校炮镜的光轴重合,A1A'1代表炮口的机械轴空间指向,B1B'1代表校炮镜的光轴空间指向,点A'1是CCD视场的中心,点B'1表示机械轴与光轴不重合时平行光光斑位置。对于空间直角坐标系OX'Y'Z',相当于对空间直角坐标系OXYZ绕X旋转α角度,绕Y轴旋转β角度,形成新的空间直角坐标系。其中,绕X轴旋转,可以对俯仰角度进行调整,绕Y轴旋转,可以对水平角度进行调整。
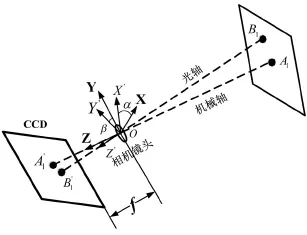
图2 同轴度模型
根据机械轴与光轴的空间关系特性,可以通过以下原理,求得二者的同轴度。
2 机械轴与光轴的三维空间特性


假设A'1先绕X轴旋转,再绕Y轴旋转,得到新的空间点A"1,其坐标为:
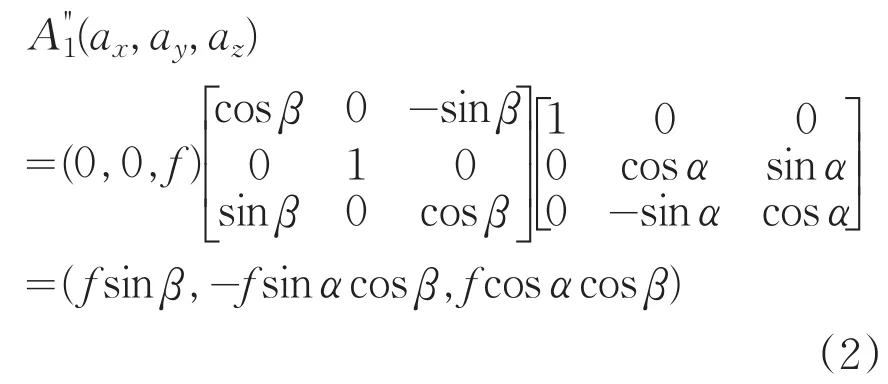




其中,α表示俯仰方向的角度,β表示水平方向的角度,二者的角度单位是秒。
通过上面的三维旋转模型推导过程,可以很好地解释机械轴与光轴的三维空间关系,表明水平方向的偏转角度,不仅受二维空间的自身角度偏转的影响,同时也受到来自于俯仰方向的偏转角度的影响,而激光准直测量方法[4],是一种基于二维空间的同轴度计算方法,它认为水平和垂直两个方向上的角度,都是通过公式(4)中计算α的思想获得,如公式(5)所示,它没有充分地考虑光轴与机械轴的三维空间关联性。

利用图像学方法,在已知图像中光斑成像点的坐标时,就可以根据公式(4)这个旋转模型,计算出光轴与机械轴在水平及俯仰方向的同轴度。
3 光斑质心提取
准确提取光斑质心坐标是基于图像处理方法测量精度的关键。首先对图像进行分割,用以梯度为基础的边缘信息引进全局阈值处理[5],得到目标的二值图像;其次,锁定目标区域;最后利用亚像素算法定位光斑质心,原理框图如图3所示。
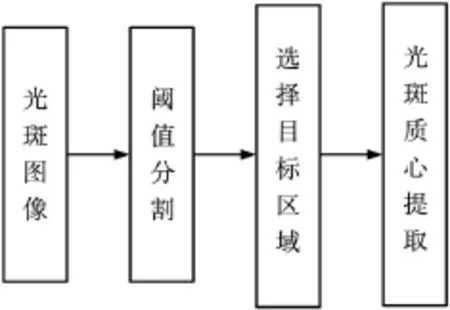
图3 光斑质心提取方法框图
观察光斑图像,它是一种典型的大背景区域上一个小物体组成的图像,其直方图将会有一个较大的波峰。设f(x,y)是输入图像,先用Sobel算子进行边缘检测,如图4所示是Sobel算子模板[6]:

图4 Sobel算子模板
获得梯度幅值图像;对其进行Otsu阈值分割,产生一幅二值图像gT(x,y),在从f(x,y)中选取对应于“强”边缘像素的下一步中,该图像用做一幅模板图像;仅用f(x,y)中对应于gT(x,y)中像素值为1的位置的像素计算直方图;用这个直方图全局地分割f(x,y),其中Otsu阈值分割公式[7]如(5)所示:

其中,T为阈值。
在二值图像上手动选取光斑区域。最后对光斑的质心进行计算,具体计算如公式(6),得到光斑质心。

4 圆轨迹的拟合技术
在以像素为单位的光斑图像中,炮口的机械轴过图像的中心点,当光轴与机械轴不同轴时,多次旋转校炮镜与标准炮口,目标的成像轨迹大致以圆形呈现,圆拟合过程如图5所示:

图5 圆轨迹拟合
其中,B'0,...,B'n表示n组光斑质心位置,Ri代表每个光轴成像点距离机械轴成像点的距离,R代表光斑质心拟合后圆轨迹的半径。在实际图像中,设A1'的坐标是A1'(xa,ya),B'i的坐标是B'i(xa,ya),则Ri及R的计算公式(7)如下所示:

其中,i代表实验次数。
这样,当我们已知一个平面圆的圆心及半径,可通过圆上任意一点带入到旋转模型公式(4)中,即可知道校炮镜与炮口的同轴度。
5 实验数据及结果分析
在实验过程中,采用分辨率是768×576,像元尺寸是8.3×8.3μm的CCD,焦距是200mm的镜头对光斑图像进行采集。采用光斑质心提取算法对图像进行处理,其过程如图6所示。其中一幅光斑图像如(a)所示;其直方图如(b)所示;首先对光斑图像进行Sobel算子边缘检测,再对其进行Otsu阈值分割,阈值为113,得到一幅梯度幅度图像(d);(e)为图(c)与图(d)之积形成的图像;图(f)是图(e)所示图像中非零像素的直方图;(g)以直方图(f)为基础,用Otsu阈值处理分割图像的结果。阈值为68,在该直方图中处在两个波峰间的位置。手动选取光斑区域,再对区域内的光斑进行亚像素质心定位,如图(h)所示。
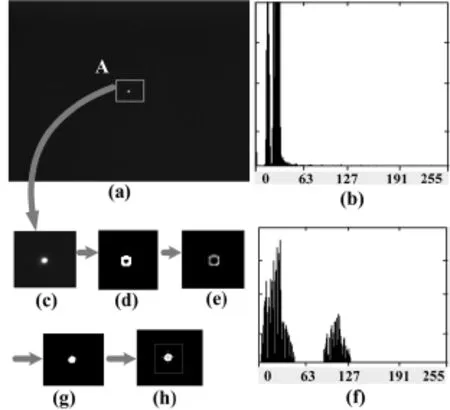
图6 光斑质心提取
在实际试验过程中进行10次操作,获得10组光斑数据,剔除距离最大值点(383.6263,288.2250)与距离最小值点(382.3358,287.8354),对剩余8组数据进行圆拟合,算得圆轨迹半径为R=0.4025个像素,圆心坐标为(384.0383,287.9463),可得光斑轨迹圆如图7所示:

图7 圆轨迹拟合
在拟合的轨迹圆上任意选择一点(384.6075,288.5155),减去偏移量(0.0383,0.0537),得到一个相对于理论中心(384,288)的点(384.5692,288.4518),将此点代入旋转模型公式(4),得知此时光轴与机械轴的同轴度为:

其中,α代表俯仰方向,β代表水平方向。
当利用激光准直方法测量同轴度时,将点(384.5692,288.4518)代入到公式(5)中进行计算,得到二者的同轴度为:

由此可以知道,利用本文推导的三维空间关系模型,表明俯仰方向偏转角度对水平方向偏转角度的影响不可忽略,此旋转模型使测量精度得到显著提高,可以很好地计算出光学系统的同轴度。
6 结论
在光电系统的同轴度测量系统中,光轴与机械轴轴线间的旋转模型、光斑质心的提取及轨迹圆半径的计算,对同轴度的测试起着十分重要的作用。本文提出的测试方法,能够高效、便捷地对光电系统同轴度进行测量,而且有效的保证了测量精度,为同轴度的测量提供了可靠、有效的依据。
[1]刘波.火炮同步精度测试系统研究[D].长春:长春理工大学,2011.
[2]蔡怀宇,李雪鹃.火炮平行性测量系统的设计[J].光学技术,2007,33(5):699-701.
[3]郑江涛.角度同步精度测量系统设计[D].南京:南京理工大学,2015.
[4]王震.基于图像处理的测角精度和同轴度测量方法[D].长春:长春理工大学,2012.
[5]Rafael C,Gon zalez.数字图像处理[M].第三版.北京:电子工业出版社,2011.
[6]白俊江,洪春勇.基于Sobel的边缘检测方法[J].电脑知识与技术,2009,5(21):5847-5849.
[7]Ma N,Wang J X.Dynamic threshold for SPWVD parameter estimation based on Otsu algorithm[J]. JournalofSystemsEngineeringandElectronics,2013,6(12):919-924.
Artillery Coaxial Precision Test Method
GAO Yangyang1,JING Wenbo2,YIN Chaoping3,WANG Xiaoman1,ZHANG Ruping1
(1.School of Electronics and Information Engineering,Changchun University of Science and Technology,Changchun 130022;2.School of Optoelectronic Engineering,Changchun University of Science and Technology,Changchun 130022;3.Continental Automotive Corporation(LianYunGang)Co.,Ltd,Changchun 130000)
Coaxial degree is an important technical index of optical system.At present,the advanced method is to use the laser collimation method to measure the coaxial degree,But it is only considered that the coaxial degree belongs to two-dimensional category,ignore its three-dimensional space,the mutual influence between horizontal and pitching direction in three dimensional space,therefore,this paper proposes a method based on 3D space modeling to test the coaxial degree.First of all,the establishment of the mechanical axis and the optical axis of the spatial relation model;secondly,facula centroid location;thirdly,the coordinates of spot images are obtained,circular trajectory fitting;finally,the circular spot trajectory coordinates of an arbitrary point substitution to the optical axis and mechanical axis of rotation model,will be awarded two coaxial precision.The experimental results show that:the influence of pitch angle on horizontal deflection can not be ignored,the accuracy of the coaxial degree measurement in horizontal direction is significantly improved.Therefore,this method has very important application value for the evaluation of the coaxial degree.
coaxial degree;high resolution CCD;spot centroid sub pixel localization;rotation matrix
TP391.41
A
1672-9870(2017)01-0089-04
2016-09-05
高洋洋(1987-),女,硕士研究生,E-mail:837027999@qq.com
景文博(1980-),男,副教授,E-mail:wenbojing@sina.com
