基于几何方法对太阳影子定位的研究
2017-03-30沈曙昀郭三敏闫旭旭朱家明
沈曙昀,王 立,郭三敏,闫旭旭,朱家明
(1.安徽财经大学统计与应用数学学院,安徽 蚌埠 233030;2.安徽财经大学外国语学院,安徽 蚌埠 233030;3.安徽财经大学会计学院,安徽 蚌埠 233030)
基于几何方法对太阳影子定位的研究
沈曙昀1,王 立2,郭三敏3,闫旭旭3,朱家明1
(1.安徽财经大学统计与应用数学学院,安徽 蚌埠 233030;2.安徽财经大学外国语学院,安徽 蚌埠 233030;3.安徽财经大学会计学院,安徽 蚌埠 233030)
目的 针对视频中物体的太阳影子与轨迹变化数据,分析太阳影子变化规律并建立数学模型,确定拍摄的地点和日期。方法 (1)对已知地点、时间与影子坐标情况下的投影问题,利用相似三角形原理建立影子长度变化模型,分析影子长度的变化规律,使用寿星天文历软件采集数据,得到模型结果。(2)对已知时间与影子坐标情况下的投影问题,对经度与纬度进行估计分析,建立模拟Analemmatic日晷模型。利用二次拟合和太阳影子长度变化规律,使用MATLAB求解,给出太阳影子定位。(3)对未知地点、时间情况下的投影问题,使用坐标系转换和空间向量建立地平系几何模型,结合模拟Analemmatic日晷模型和二次拟合方法,利用MATLAB求解,得到时间与太阳影子定位的经纬度值。结果 (1)2015年10月22日北京时间9∶00~15∶00时之间天安门广场3 m高的直杆的太阳影子长度变化曲线图,曲线端点:9∶00,影子长度为6.59 m;15∶00,影子长度为6.70 m。曲线最低影子长度为3.58 m,此时时间为12∶13。(2)文献[1]中直杆所在的地区为111.04 °E与4 °N以及111.04 °E 与29~35 °N范围内,直杆可能处在中国南海、常德市、十堰市、商洛市和宜昌市。(3)文献[1]日期为9月26日,直杆位于塔吉克斯坦;日期为1月1日,直杆位于中国南海。结论 通过分析视频中太阳阴影轨迹的几何属性来进行地理位置估计计算,利用几何关系建立3种模型,对问题进行由浅入深的分析。在3D角度和测量条件未知的情况下也可以使用上述研究方法,这使得该方法具有广泛的应用和更大的灵活性。
太阳影子定位;模拟Analemmatic日晷模型;二次拟合;MATLAB
随着网络的进步,越来越多的人将自己生活的所见拍摄成视频发布到网络上,但多数视频的拍摄地点和拍摄日期无法确定。于是如何确定视频的拍摄地点和拍摄日期成为视频数据分析的一个新的研究课题。太阳影子定位技术就是通过分析视频中物体的太阳影子变化,确定视频拍摄地点和日期的一种方法[1]。目前,国内对于太阳影子定位问题的研究相对较少,而国外的研究成果较为丰富。Van Gool等人研究了阴影机型物体的模式识别[2];Kriegman和Belhumeur[3]提出了投影物体结构与阴影之间的几何关系;除此之外,还有对户外相机进行校准的研究方法,例如文献[4]和[5]阴影对于视频理解是很重要的对象,这是因为它能提供重要的几何线索,但是在3D 视觉应用中阴影问题没有得到广泛的关注。目前为止,经纬度估计的方法主要有3种类型:基于特征匹配的方法;光度测量方法;几何测量方法。本文根据文献[1]中所提供的数据,利用几何方法与Analemmatic日晷投影原理来分析影子长度变化与时间和地点之间的关系,建立相关模型以实现太阳影子定位。
1 分析太阳影子长度变化的规律
1.1 研究思路
为了便于研究视频中太阳影子的变化,首先给定假设: 太阳光线不受云层、地形等因素的影响,直杆延长线经过地心,假设所有数据来源科学、准确;其次,就相关知识构建空间坐标系;最后结合全国大学生数学建模竞赛A题所给的数据进行拟合,可求得太阳影子长度的变化规律。
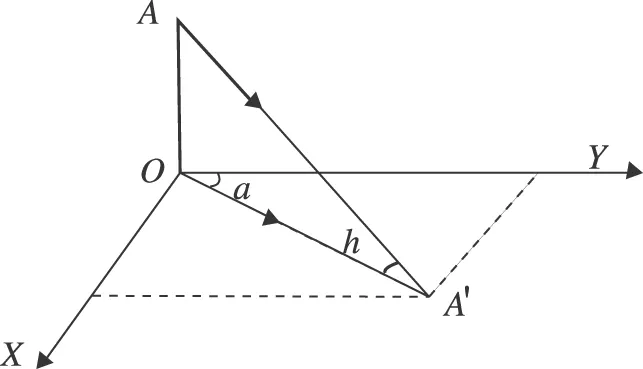
图1 太阳光平面投影坐标图
1.2 研究方法
在地平坐标系中(见图1),h为地平纬度(也称太阳高度角),地平线以上为正,地平线以下为负。α为地平经度(也称方位角)。
太阳赤纬角以年为周期,用δ表示,范围为[+23 °26′, -23 °26′]。太阳时角用ω表示,规定中天(经过当地子午圈的时间)时角为0 °,上午时角为负值,下午时角为正值,每小时时角变动为15 °[6]。
研究太阳和地球的运动一般采用地平坐标系和赤道坐标系,根据《天文算法》中坐标变换的描述[7],计算本地地平坐标公式:
tan(a)=sin(ω)/(cos(ω)sin(φ)-tan(δ)cos(φ))
sin(h)=sin(δ)sin(φ)+cos(δ)cos(φ)cos(ω)
(1)
根据三角形边角关系和太阳高度角的计算公式[8],影子长度变化模型有:
(2)
其中影子长度L′=A′,φ为测量点O的纬度。
根据天文学中固定指标计算公式[9],则有公式(3)和(4):
(3)
ω=15(ST-12)
(4)
其中n为日期天数,ST为真太阳时,即为测量点的当地时间。
1.3 结果分析
结合公式(2)、(3)、(4)得:太阳高度角直接决定影子的长度,当太阳高度角h越大,影子长度越短;反之影子长度越长。当δ与ω固定,φ越接近太阳直射点的纬度,影子长度越短。当φ与ω固定,δ不断增大,影子长度减小至最短;δ不断减小,影子长度不断增加到最长长度。当φ与δ固定时,ω不断增大,影子长度增加;反之影子长度减少。
根据模型求解2015年10月22日北京时间9∶00~15∶00时天安门广场(39 °54′26′′N,116 °23′29′′E)3米高的直杆的太阳影子长度。使用寿星天文历软件采集北京时间9∶00~15∶00时之间对应时间点的δ、ω数值,取步长为900 s。10月22日时,n=295。已知L=3,使用Excel计算得表1:
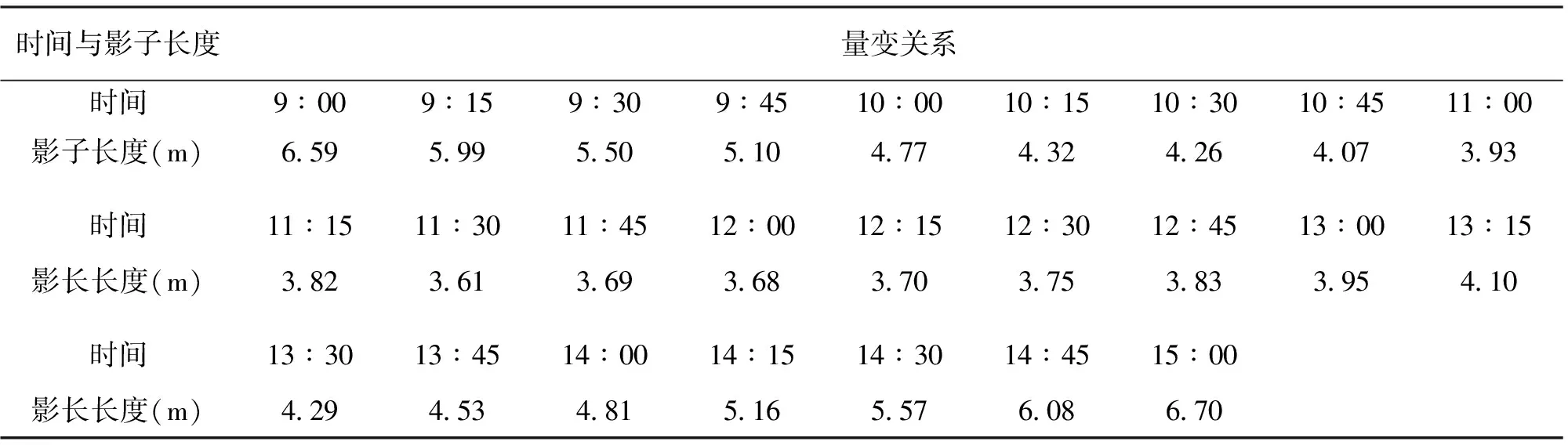
表1 时间与影子长度变化表
使用Excel作图,得到太阳影子长度变化曲线图,如图2。

图2 太阳影子长度变化曲线图
由图2知,9∶00时,影子长度为6.59 m,15∶00时,影子长度为6.70 m;曲线最低影子长度为3.58 m,此时时间为12时13分。
2 基于模拟Anemmatic日晷模型太阳影子定位中经纬度的确定
2.1 研究思路
首先分别对经度与纬度进行分析,得到相关的计算公式;其次,对文献[1]中数据进行二次拟合,利用太阳影子长度变化规律,得到最小影子长度对应的测量点时间;最后,将最小影子长度对应的测量点时间带入公式中,利用MATLAB求解,可以给出太阳影子定位。
2.2 研究方法
1)经度计算
测量点的经度=最高太阳高度角下时间对应的时角+标准时间所对应时区的中央子午线经度。对数据进行二次拟合可以得到最小影长对应的测量点时间。测量点的经度计算公式:
γ=γ′-15(ST-T)
(5)
其中γ′为标准时间所在区间的中央子午线经度,为标准时间,此处为北京时间。
2)纬度计算

图3 指示立杆投影
如图3所示,建立投影日晷方位图,指示立杆位于A点,影长为AB,交于投影日晷得时间线为AC。有OD=AG=sinω,CD=sinφcosω,指示立杆A点距O点的距离OA=DG=tanδcosφ。根据平行线等分线段定理得:
(6)
已知影子在地平坐标系上的x、y坐标,求得不同时间段影子的长度。将时间数值化,利用Excel对时间与影子长度的数值进行二次拟合,得到图4。

图4 时间与影子长度拟合图
由图4知,时间(t)与影子长度(L′)的函数式:
L′=0.1489t2-3.7519t+24.128
当L取最小值时,ST=t=12.598 7。以北京时间作为标准时间,其中央子午线位于东经120 °,4月18日正午时间T=12。由公式(4)换算后的时角公式为ω=15 °(MT-12.598 7)。利用寿星天文历软件取得数据,其中步长取180s。根据公式(6),设sinφ=Z,则:
2.3 结果分析
考虑到一元二次方程aZ2+bZ+c=0的系数在变化,利用MATLAB进行编程求解,求出sinφ与φ。
结合所求的经纬度,在地图上对求得的经纬范围进行划分。根据谷歌地图定位的范围圈定,得到1个区域和4个可能区域,分别为中国南海、常德市、十堰市、商洛市和宜昌市。
3 基于地平系几何模型对未知时间情况下的影子定位
3.1 研究思路
首先,结合空间向量与地平系几何模型,利用几何分析方法对未知时间下的太阳影子变化问题建立影子定位模型;其次,对文献[1]中相关数据进行二次拟合,得到最小影长对应的测量点时间;最后,结合模拟Anemmatic日晷模型,利用MATLAB求解[10],可以给出时间与太阳影子定位的经纬度值。
3.2 研究方法
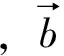
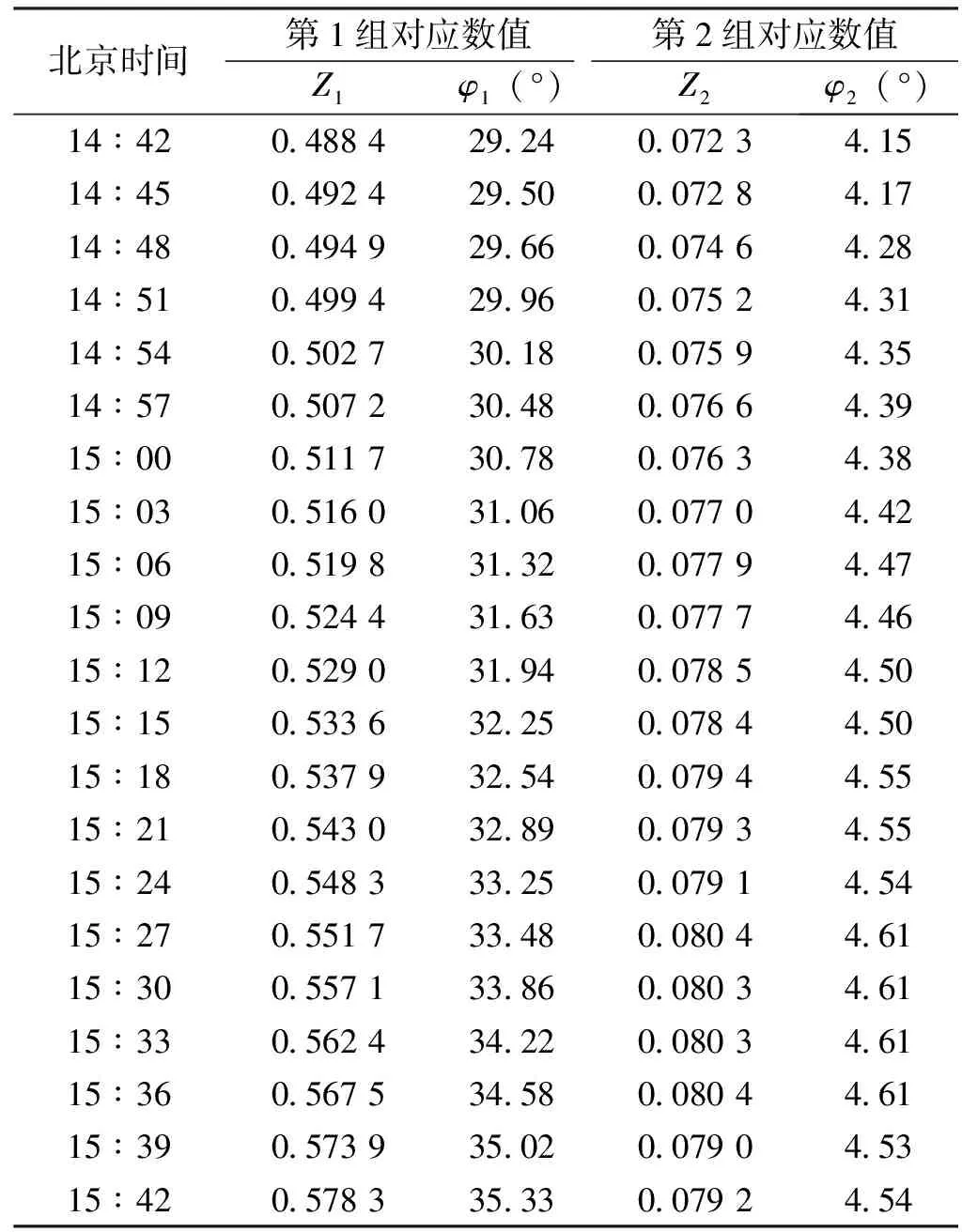
表2 z值及对其应的地理纬度φ数值表

图5 地平坐标系几何模型图
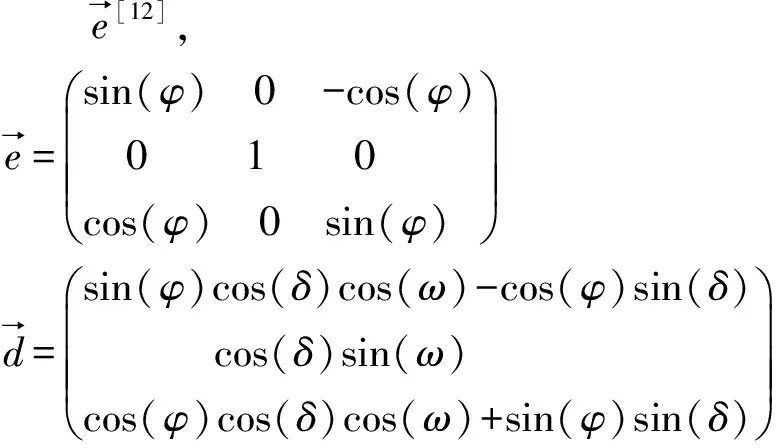
地平坐标系几何模型:地平坐标系的地平面原点是观察者所处的位置,指示立杆和太阳的坐标都转换为地平坐标系,进而利用日晷投影的原理求出指示立杆的经纬度和测量日期。

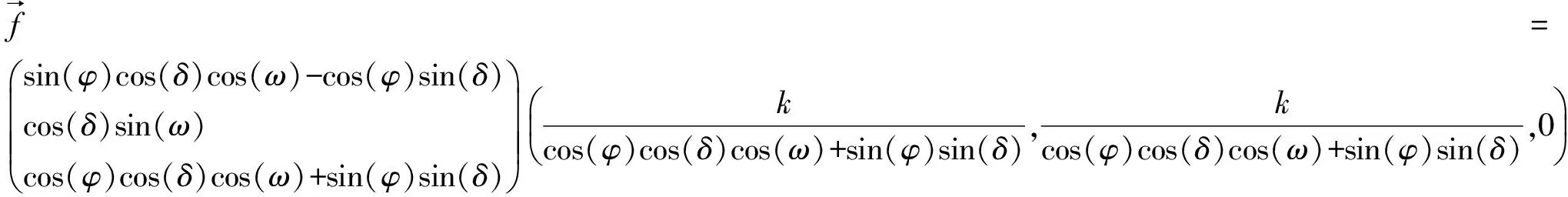

(7)

(8)
由附件2和附件3的影子在地平坐标系上的x、y坐标,利用勾股定理求得不同时间段影子的长度。将时间数值化,利用Excel对时间与影子长度的数值进行二次趋势拟合,得到图6。
由图6知,时间(t)与影子长度(L′)的函数式为:
L′=0.0981t2-2.985t+23.319
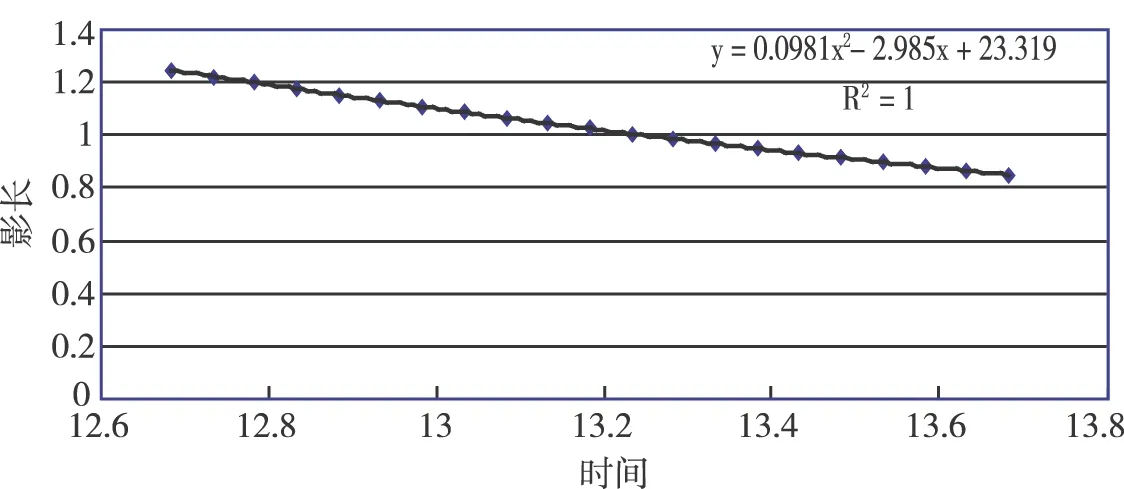
图6 拟合曲线
当L′取最小值时,t=15.2141,L′=0.6120。以北京时间作为标准时间,其中央子午线位于东经120 °,即T=12。利用公式(5)计算得γ′=71.79E。根据时角公式,可得测量地时角公式为:
ω=15°(ST-15.2141)
利用Excel求得原数据中每个时刻的时角ω,cosω都趋近于1,所以把公式(7)简化:
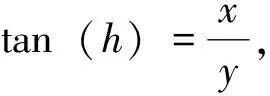
3.3 结果分析

同理,对附件3中数据进行二次拟合,得到时间(t)与影子长度(L′)的函数式:
L′=0.2964t2-7.5507t+51.564
当L′取最小值时,ST=t=12.7373,L′=3.4760。L=12,γ=108.94E。当L取4 m,日期为1月1日,利用谷歌地图可查(1 °N,108.94E),处于中国南海区域。
4 结束语
本文的主要研究工作是通过分析视频中太阳阴影轨迹的几何属性来进行地理位置估计计算,利用几何关系建立3种模型,分别对已知时间与地区条件下影子长度变化问题、已知时间与影子长度变化条件下地区分布问题和已知影子长度变化下地区与时间确认问题,进行了由浅入深的分析,得到较为准确的结果。在3D角度和测量条件未知的情况下也可以使用本文的研究方法,这使得本文的方法具有广泛的应用和更大的灵活性。但是由于较多涉及到几何处理与公式转化,模型计算量较大,若处理不当,会使得计算误差较大。同时需注意,北京时间与北京本地时间是不同的两个概念。上述研究方法经过适当修改,可以运用到天文、地理方面的定位问题。为实际测量太阳影子(不仅局限于杆的影子)的问题提供了一个较为科学的方法,在地理测绘中可以发挥了一定的作用。参考文献:
[1]中国工业与应用数学学会.全国大学生数学建模竞赛A题[EB/OL].http://www.mcm.edu.cn/html_cn/node/ac8b96613522ef62c019d1cd45a125e3.html.2015-09-10.
[2]Van Gool L,Proesmans M,Zisserman A.Planar homologies as a basis for grouping and recognition[J].Image Vis Comput,1998,16,21-26.
[3]Bouguet J,Perona P.3D photography on your desk[A].IEEE,Proceedings of the IEEE ICCV,IEEE Computer Society[C].Santa Clara:IEEE Xplore Digital Library,1998,43-50.
[4]Antone M,Bosse M.Calibration of outdoor cameras from cast shadows[A].IEEE,Proceedings of the IEEE International Conference on Systems,Man and Cybernetics[C].Shanghai:IEEE Xplore Digital Library,2004,3040-3045.
[5]Cao X C,Foroosh H.Camera calibration and light source estimation from images with shadows[A].IEEE,Comput Vis Image Understanding[C].Aberdeen:IEEE Xplore Digital Library,2007, 4 (02): 127-140.
[6]武琳. 基于太阳阴影轨迹的经纬度估计技术研究[D].天津:天津大学,2010.
[7]Meeus J.Astronomical Algorithms[M].2nded Richmond:Willmann-Bell Incorporated:1998:81-90.
[8]Cao X C,Foroosh H.Camera calibration using symmetric objects[A].IEEE,IEEE Trans Image Process[C].Anaheim:IEEE Xplore Digital Library,2006,15(11):3614-3619.
[9]好搜百科,太阳高度角[EB/OL].http://baike.haosou.com/doc/4128005-4327467.html.2015-09-10.
[10]赵志升,罗德林,李海英.数据挖掘技术与应用[J].河北北方学院学报:自然科学版,2006,22(06):63-66.
[11]百度百科,投影日晷[EB/OL].http://baike.baidu.com/link?url=cud3U4UDXkQSA8FJrRwNyo4aBdxkjPaMnFX3y_hYNZkx1fbHWMw6c7PEkhhwjS4nzi7FpuVt-piq8Of0gudmSln3YPIuZ4dIS_Kt8yUHeinEzS5zKU0ZfY7RYAhhIhWM,2015-09-10.
[12]刘来福,何青,彭芳麟,等.用Maple和MATLAB解决科学计算问题[M].北京:高等教育出版社,1999:318-321.
[13]百度文库,探究如何用影子的长度和身高计算纬度[EB/OL].http://wenku.baidu.com/view/e4db2a14af1ffc4fff47ac67.html.2015.
[责任编辑:刘守义 英文编辑:刘彦哲]
Solar Shadow Positioning Based on Geometric Techniques
SHEN Shu-yun1,WANG Li2,GUO San-min3,YAN Xu-xu3,ZHU Jia-min1
(1.School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu,Anhui 233030, China;2.School of Foreign Languages,Anhui University of Finance and Economics,Bengbu,Anhui 233030,China; 3.School of Accountancy,Anhui University of Finance and Economics,Bengbu,Anhui 233030,China)
Objective In view of the sun’s shadow and track changing of data of the object in the video,the changing rule of the sun’s shadow was analyzed and the mathematical model was established to determine the filming location and date.Methods (1)For a projection problem with known location,time and shadow coordinates,by using similar triangle principle to establish a change model of shadow length,the variation of the shadow length was analyzed,and the model results were obtained from data acquired by using the software-the longevity of the astronomy and calendar;(2)For the projection problem with known time and shadow coordinates,by evaluating the longitude and latitude,the sundial model of simulated Analemmatic was establish.By using the quadratic fitting,variation of sun shadow length and the MATLAB,the positioning coordinates of sun shadow were obtained.(3)For the projection problem with unknown location and time,by using coordinate transformation and space vector to establish horizon line geometric model,combining analog of Analemmatic sundials model with quadratic curve fitting method,and using MATLAB,the time and longitude and latitude values of the sun shadow position were obtained.Results (1)Between 9∶00-15∶00 of October 22,2015 Beijing time,the sun’s shadow length variation curve,and the curve ends of the 3-meter-high straight rod on Tiananmen Square were:on 9∶00,the shadow length was 6.59 m; on 15∶00,shadow lengths 6.70 m; on 12∶13 the curve for the lowest shadow lengths was 3.58 m. (2) In literature [1] the straight rod was located in the area between 111.04°E,4°N and 111.04°E,29°-35°N,and the straight rod might be in the South China Sea,Changde city,Shiyan city,Shangluo city and Yichang city.(3)In literature [1],on September 26,the straight rod was located in Tajikistan;on January 1,the straight rod was located in the South China Sea.Conclusions By analyzing the geometric properties of the sun shadow track in video to estimate location,three models were established by using the geometric relationship,and the problem was gradually analyzed.The research method of this paper applies to the condition with unknown 3D angle and measurement,which allows the method to have wide application and greater flexibility.
solar shadow positioning;sundial model of simulated Analemmatic;quadratic fitting;MATLAB
国家自然科学基金项目(11301001);安徽财经大学教研项目(acjyzd201429)
沈曙昀(1996-),女,安徽合肥人,安徽财经大学统计与应用数学学院在读学生,研究方向:应用统计学。
朱家明(1973-),安徽泗县人,副教授,硕士,研究方向:应用数学与建模。
O 242
A
10.3969/j.issn.1673-1492.2017.01.005
来稿日期:2016.05.11
