分形编码在人脸识别中的应用
2017-03-30陈云花章星
陈云花 章星
摘要:随着科学技术水平的大力发展与改进,怎样对人脸图像展开编码、识别、检索成为图像信息领域内一个较为热门的话题。针对一个大型的人脸库而言,一般首先需要对每一幅人脸展开压缩,以此对储存空间进行节省。文章分析了分形编码在人脸识别中的具体应用,并对目前的分形技术用于人脸识别方法进行了研究。
关键词:分形编码;人脸识别;人脸图像;图像信息;对称性;方差 文献标识码:A
中图分类号:TP391 文章编号:1009-2374(2017)03-0057-03 DOI:10.13535/j.cnki.11-4406/n.2017.03.025
1 目前的分形技术用于人脸识别方法
1.1 分形近邻距离法
分形近邻距离法主要是来源于分形代码吸引子以及欧氏距离的唯一性在第一次提出了分形近邻距离的概念之后,能够有效针对任意的初始输入图像I,运用图像X的分形代码展开有限次的迭代之后,I可以把X的吸引子进行收敛。但是因为分形编码本身具有较高的连续性,如果运用X或者和X相近似的图像,就像相对于同一个人的不同人脸图像而言,作为输入,在一次迭代的基础上,获得的结果图像将和输入图像较为近似。另外,运用其他的图像,就像相对于不同人的人脸图像来说,作为输入,在一次迭代的基础上,获得的结果图像却与输入图像相差很大。在这个事实的前提下,相关的工作者把将分形近邻距离法大力的运用于特定的ORL人脸库上,展开科学的识别分析,然而平均识别率仅是90%。要想有效的强化识别效率,在实际的分形编码工作之前,第一步需把输入图像展开4个方向的旋转步骤;第二步需充分考虑到人脸的不同部位,会影响对人脸的识别,需要把权值加入分形近邻距离法中,适时提出了一种特征匹配方法,即“局部—全局”,也就是加权分形距离法,进一步帮助识别率的大力提高,然而算法的复杂性也在一定程度上有所提高。
1.2 分形特征法
人们主要是在块的图像分形代码中,将定义域块旋转方向进行提取,同时也相应的提取出和值域块匹配的定义域块位置,挖掘出亮度因子、对比度因子等相关参数,并且在此基础上构建4个特征向量,将其当作图像的表征,从而促进对人脸的识别。然而该类方法与分形近邻距离法相比,不具有优越性。
1.3 分形与其他方法相结合
人们对以上两种方法进行了有效的改进,将其和主成分分析方法有机地进行了结合,相应得到了一个对人脸表情变化情况具有良好稳定性的人脸识别系统。借此人们在分形近邻距离的条件下,随之提出了分形奇异值近邻距离这一概念,进一步把局部奇异值分解与分形编码两者进行了有效的结合,相应增强了识别率。然而该类方法由于本身不是一种运用纯分形技术来展开人脸识别活动,所以其产生的结果无法与纯分形技术方法
比拟。
1.4 像素链法
此类方法主义运用的是“图形—理论”的思想,在分析图像的分形代码的基础上,得到像素链,而这种像素链代表的就是像素间的内在联系,同时有效定义了距离度量,进而便于人脸识别。另外,人们在大量实验证明的基础上总结出了一定的经验。然而,由于人们的研究活动对像素链产生过程的描述较为模糊不清,在实际的分形编码过程中,并未能充分说明是否展开压缩变换,也没有证明如何得到仿射变换参数等内容。
1.5 眼睛定位
人们把分形技术大力的运用于人眼定位中,这种方法也作为有效进行人脸识别的基础。为了进一步提高人脸识别率,在“图形—理论”思想的基础上,相应提出了一种运用分形编码图形来表示的人脸识别方法。该种识别方法主要是运用像素块来作为识别基元,对分形编码过程中在没有空间上压缩和有压缩两种不同的条件下的具体情况进行了进一步的讨论,对如何计算每个像素块的仿射变换参数a和b因子也进行了充分的研究。同时在分形编码的实际计算过程中以及在图形表示的生成过程中融入了一定的旋转变换步骤,获得了良好的人脸识别率。
2 基于对称性与方差的快速分形人脸图像压缩算法
2.1 基于方差的分形图像编码法
假设被编码图像I被分为互不重叠块,也就是值域块Ri,通常Ri能够取4×4、8×8、16×16等,第一步:需要把I分为若干定义域块Di,该尺寸一般比Ri大,能够满足实际的收敛要求,要想让Di可以和Ri进行对比,需要把Di收缩到和Ri一样的大小程度,把经过收缩之后的全部Di进行表示,即{Di}(i=1,2,…,n);第二步:每一个Ri,由{Di}中获取Di进行仿射变换,进一步挖掘出最优良的匹配块了,若是Di和Ri距离是最小的情况下,Di也就是Ri的最优匹配块。在实际的编码过程中,需要把仿射变换参数进行有效的记录,以便来获得此图像的分形码,并进行表示,即{xi,yi,Li,si,gi},而xi、yi作为定义域块Di的起始位置,si、Li、gi三者也分别作为对比度因子、对称变换参数、亮度偏移因子。在此基础上,人相应提出了基于方差的分形图像编码法,也就是在求仿射变换前,第一步对{Di}进行求方差{eDi},同时对{Di}依据eDi排序,针对每一个Ri而言,求Ri的方差eRi,依据预先明确的w,接着把Di明确在比eRi分别大(w/2)%以及小(w/2)%的范围中,并且在其中挖掘出最优良的匹配块,此方法主要是在降低定义域块数目的前提下来实现通过编码速度的要求。然而此算法主要是相对一般图像而言的,并不是针对于特定的人脸图像,所以需要在前人研究的基础上,进一步有效地提出了针对人脸图像的分形图像压缩算法。
2.2 人臉图像的分形码算法
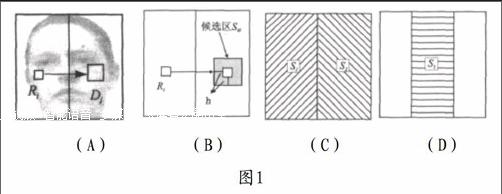
人脸图像的分形码其实就是一组压缩映射关系,主要是把定义域块变换至对应值域块,同时定义域块的形状能够选取正方形、长方形、三角形,而且其定义域块尺寸能够固定也可以变化,以上这些内容若是方式改变均会对最终的分形码带来一定的影响,更有甚者,若是输入图像中出现细微的改变,也同样会造成分形码内少数的参数发生变化。鉴于此,这就需要帮助分形码不随着人姿势变化以及人脸表情而出现相应的改变。本文所涉及的算法,主要是运用人脸本身分布具有一定的对称性来对定义域块所在范围的进行限制。
因为人脸图像本身就有左右的对称性,所以针对值域块Ri而言,一般能够在人脸对称的区域内挖掘出和人脸匹配的定义域块Di,详见图1(A)所示,然而因为人脸一般具有相关的表情或者姿势的改变,这就致使人脸的对称线有可能不是位于人脸部的中央,然而在实际对匹配块接着挖掘的过程中,能够略微将候选区域范围进行扩大,一般可以达到Si 0区,详见图1(B)所示,位于候选区Si 0内还是没有寻找到匹配块,这就需要依据值域块Ri处于的具体位置,把候选区分别进行扩大,达到S1区、S2区以及S3区,详见图1(C)、(D)所示。其实也就是在S1区内存在假定值域块Ri,那么候选区就会相应的扩大到S2区,就像值域块Ri位于S2区内,那么候选区就会扩大到S1区中,也就像值域块Ri位于S3区内,这就说明Ri是位于人脸中间的,所以需要把候选区扩大到S3区。鉴于此,相应提出了人脸图像压缩算法,也就是假设候选区Si 0是位于值域块Ri的对称位置上,同时S1区位于人脸图像的左半区域,尺寸比Ri大h,详见图1(C)。人脸图像的中间三分之一区域也就是S3区,人脸图像的右半区域也就是S2区,假设阈值为T。即第一步:对{Ri}是否为空进行判断,若是对所有Ri全部编码完,就需要退出,否则从其中取一Ri;第二步:将Ri的对应方差假设为eRi,把Di明确为Si 0区,同时eDi比eRi均大,差范围维持于(w/2)%之间,此范围通常表示为{Di 0};第三步:在{Di 0}中一一取出Di,并且和此前的Ri进行仿射变换,并且与之展开对比,若是Ri、Di两者的距离与阈值T相比要小,就需要明确Di作为目前最优的匹配块,将其位置及各仿射参数进行记录,就需要返回至第一步;第四步:如果是在{Di 0}内,Ri、Di两者的距离都比阈值T要大,这就需要按照目前的Ri位置,把候选区进行扩大,需要达到S1、S2、S3三个区的一个,同时eDi比eRi分别大(w/2)%与小(w/2)%的范围中,把此范围进行表示,即{Di 1};第五步:在{Di 1}内一一将Di取出,并且有效和目前的Ri进行仿射变换对比,若是Ri、Di两者的距离与阈值T相比要小,就能够明确Di,并且作为现如今最优匹配块,将其位置及各参数进行记录,返回第一步;若是在{Di 1}内,Ri、Di两者的距离与阈值相比,均大,这就需要与{Di 0}、{Di 1}内有效的选取最小距离对应的Di,并且将其作为如今最优的匹配块,对其位置及各参数进行记录,继而返回第一步。
假设处于最糟的环境下,也就是对全部被值域块都没有于候选区Si 0中找到相应的匹配块,但候选区已经被扩大至人脸图像的二分之一,这就需要运用此算法中所需要编码时间能够达到传统方法的二分之一,则说明了运用本文算法,编码速度令人满意。
3 基于分形码的人脸识别算法
分形码的表示:于分形码{xi,yi,Li,si,gi}内,xi、yi参数对某一值域块进行了充分的反应,在和其最匹配的定义域块的位置上,xi、yi对定义域块的绝对位置也展开了充分的反应,但是和值域块所处的位置并没有太大的关系,在实际的分形解码工作中,能够直接运用此参数获得一个正确的解码图像。与此同时,在具体的识别过程中,需要把xi、yi进行有效的转变,即向着类似于极坐标的θi、di来进行表示,θi、di表示的其实就是定义域块、值域块间两者之间的夹角和相对距离。在di较小的情况下,则说明在自身附近内值域块挖掘到了匹配块;若是在di较大的情况下,这就说明了只有在一个较远的地方才能够与此前值域块相似的块。而若是一幅图像的分形码内di均不大,这就表明了在自身附近内值域块挖掘到了匹配定义域块的机会较大,另外也充分地说明了在自身附近匹配块出现的频率也较高。通过幅角意义可以知道,θi其实就是对图像匹配块发生于哪一方向的表示,如果分形码中大多数θi的取向较为相同的情况下,很大程度上也就说明了图像纹理具有很大的方向性。与此同时,Li是对匹配块间的几何对称变换关系的有效反应,都是gi、si二者则充分则展现了图像对比度的差异性。
4 结语
分形编码本身作为一项复杂的工作,本文主要是在基于对称性与方差的快速分形人脸图像压缩算法的基础上,针对人脸自带的对称特性,相应提出了基于分形码的人脸识别算法,此方法得到的识别率较高,值得进一步得到应用。
参考文献
[1] 赵德平,鄭莹.Carotid-Kundalini函数和Logistic映射
在分形编码中的应用[J].计算机应用与软件,2008,
25(5).
[2] 姬光荣,曲翠璐,赵文仓,等.基于分块分形编码的
多姿态、表情人脸图像检索[J].中国海洋大学学报
(自然科学版),2004,34(5).
(责任编辑:蒋建华)
