污水处理系统溶解氧的改进GPC-PID控制算法
2017-03-29刘向,赵敏
刘 向,赵 敏
(上海理工大学 光电信息与计算机工程学院,上海 200093)
污水处理系统溶解氧的改进GPC-PID控制算法
刘 向,赵 敏
(上海理工大学 光电信息与计算机工程学院,上海 200093)
针对污水处理过程中,溶解氧浓度实时变化难以控制的问题,提出一种基于改进GPC-PID的DO值控制算法。通过改进GPC-PID算法的滚动优化原理,系统能够在线自整定PID参数,在溶解氧浓度达到稳定状态时无需反复求解Diophantine方程。改进后的算法减少了方程的求解次数和复杂度,降低了系统的运算量,同时解决模型时滞带来的控制问题。仿真结果表明,运用改进的GPC-PID预测控制算法能获得较好控制效果,同时提高了系统的稳定性和优化计算的快速性。
溶解氧浓度;污水处理;预测控制;广义预测控制PID
溶解氧(Dissolved Oxygen,DO)的浓度是活性污泥法污水处理曝气过程中重要的运行参数。曝气池中溶解氧浓度的高低较大程度上直接影响着出水水质,因此对DO值的控制对于提升活性污泥法水处理技术水平和能效具有重要的现实意义[1]。如今国内外的专家学者对污水处理系统DO值的控制算法进行了深入研究,提出来一系列的控制方法。如文献[2]提出了一种基于双层优化结构的加权区间预测控制方法。设计一种融合溶解氧区间控制和曝气能耗指标的双层目标优化控制策略。文献[3]为提高污水处理效果,设计线性自抗扰控制器以达到主动抵抗外部干扰、提高溶解氧浓度控制效果的目的。文献[4]提出一种溶解氧浓度的神经网络预测控制器设计方法。通过3层BP神经网络训练出系统神经网络逼近模型。设计满足出水水质指标的溶解氧约束预测控制器,将所设计的控制器用于污水处理DO值的时变设定值跟踪控制。
在满足出水水质的前提下,以上方法基本可以对溶解氧浓度进行控制,有效跟踪溶解氧设定值,但是仍存在一些问题,如控制模型必须满足一些前提的限制、较少考虑实际过程中外部因素对系统的干扰、对于模型时滞性带来的问题、控制算法的复杂度较大等问题。综合广义预测控制与PID控制两种方法的优点,本文提出一种改进的GPC-PID控制算法的溶解氧控制方法。
1 水处理系统DO值控制模型的建立
在活性污泥法污水处理过程中起到关键处理效果的因素是生化反应池中的溶解氧浓度(DO值),而DO值的控制是通过控制曝气装置进行控制的。因此本文选择对生化反应池中的曝气量大小进行控制,将生化反应池中的DO值作为被控量,在线实时监测生化反应池的溶解氧浓度,并根据平衡DO浓度的大小来判断污水有机物的高低进而及时地控制曝气量,使得DO值保持在2 mg/L。污水处理过程中曝气池中溶解氧浓度的预测控制模型如图1所示。

图1 GPC-PID的DO浓度预测控制模型流程图
采用改进后的GPC-PID控制算法建立模型对DO值进行预测控制,以在线DO检测值y(k)为控制器的输入量,改进后的GPC-PID控制器向调节曝气量的控制端输出为控制量u(k),调节鼓风机的曝气量,来改变生化反应池好氧区的溶解氧浓度。
2 溶解氧的GPC-PID控制器设计
在对溶解氧含量的控制过程中,根据在线DO检测准确分析,得出最优控制量,才能保证对于溶解氧含量的控制达到理想的预测控制效果。这就需要控制目标准确、快速的跟踪设定值,满足控制需求。传统的PID控制不能获得良好的控制效果,通常还要与其他自整定控制算法结合作用于被控对象。而广义预测控制算法对于模型的要求低,以保持广义最小方差、在线辨识等原理的基础上,并在优化过程中汲取了MAC、DMC中的多步预测优化策略[5]。当系统的溶解氧含量发生较大变化或系统出现时滞问题不能够获得当前被控量,但是由于模型预测控制方法需要建立被控对象的精确模型,且模型预测的精度对模型预测控制器的性能有较大影响,所以该方法在非线性系统控制中的应用受到限制预测控制算法与PID相结合构成了一种新的控制器,如图2所示。
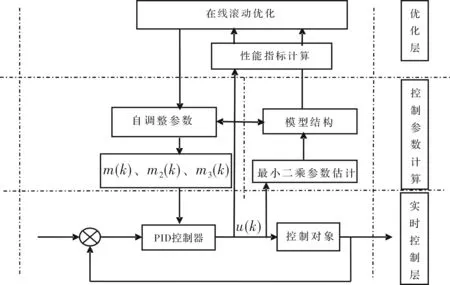
图2 控制系统结构图
2.1 GPC-PID控制算法
GPC-PID控制算法的控制结构分为两层,包括底层PID控制回路和上层GPC优化回路,基本PID控制层是普通的PID控制器,对于此系统需要调节整定的参数仍然是kpkikd但在实际使用中,溶解氧的控制过程有很复杂,具有非线性、不确定时变性、纯滞后性等特性。在负载、噪声等各种随机干扰的影响下,过程参数都会随时变化,这就需要在PID参数能够在线调整来满足实时控制的要求。优化的性能指标是基于多步预测信息的GPC性能指标,既要能保证输出能够准确跟踪设定值,并且被控量的变化不能过大。优化层回路含有两个模块分别为辨识模块和控制模块。辨识模块根据已有的被控对象模型,经过滤波、线性处理等,得到不同工况下的被控对象的实时CARIMA模型;控制模块,先检测系统的性能指标是否在合适的范围,若不合适,根据被控对象的模型重新运算预测输入与参考输入的偏差,采用滚动优化策略,通过最小化PID控制层参数的性能指标,得到最优的PID控制层回路的参数。
2.2 GPC-PID控制算法PID控制回路
一般增量型PID控制器的结构形式为[6]
Δu(k)=m1e(k)+m2e(k-1)+m3e(k-2)
(1)
其中,m1=kp+ki+kd,m2=-kp-2kd,m3=kd。
式(1)也可以写成如下结构
(2)
式中,MT(k)=[m1(k)m2(k)m3(k)]。系统被控模型仍采用CARIMA的形式[5]
A(z-1)Δy(k)=B(z-1)Δu(k-1)+ξ(k)/Δ
(3)
将式(2)带入式(3)得
(1-z-1)A(z-1)y(k)=B(z-1)WT(k)e(k)+ξ(k)
(4)
为得到系统的向前j步预测,为此引入Diophantine方程[7-8]
(5)
通过式(3)与Diophantine方程,利用GPC算法,再根据已知输入、输出、未来的输入值,可以得到预测被控对象的最优j步未来输出
Fj(z-1)y(k)+Hj(z-1)Δu(k-1)
(6)
将等式(6)代入系统的性能指标得
(7)
式中,N为预测时域;Nu为控制时域,表示被控变量在Nu步后将不再改变。
标准GPC控制器控制变量可写成
Δu(k)=(GTG+λI)-1GT(ω-Fy(k)-HΔu(k))
(8)
将等式(8)写成以下矩阵的形式
(9)
(10)
最优控制序列Δu(k)可表示为[9]

(11)

(12)
综上所述,根据广义预测控制的性能指标和被控对象的CARIMA模型可以直接得到底层PID控制回路层的参数调整规律。再由GPC的滚动优化与在线辨识,可以优化系统性能,然后得到最优的PID控制器参数,由此得到了具有GPC性能的PID结构新型控制器。
3 GPC-PID控制算法改进
以上所述的GPC-PID控制算法解决了PID参数在线自整定的问题,但在此过程中线滚动优化是一直进行的,换句话说PID自整定参数在实时的滚动调整。但是当污水处理系统的DO值达到稳定程度后,PID的控制参数一般不再需要改变,只有当系统的DO值在外界因素干扰下发生改变时,才要重新整定参数。所以前面讲述的控制方法在任意时刻都可以得到最优的PID参数,可是这样会带来诸多不必要的计算,给系统带来负担。对于以上问题,对算法进行改进来降低算法的计算量就显得很有必要。
首先,要定义和评估系统当前的性能。在满足这些性能的基础上,再调用GPC优化算法调整PID控制参数,来获得期望的DO值控制。由于系统存在很多实时动态的负载或干扰因素,所以系统的具体设计应含有稳态误差指标和时域响应指标。本文提出以下几个指标分别为振荡幅度、超调量、残差、衰减率。设衰减率定义
(13)
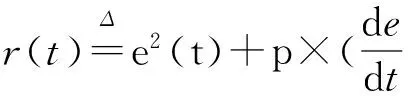

本文使用衰减率hr作为系统状态的判断依据,基于GPC算法的优化层回路。是否启动优化层分为两种情况:
(1)若当hr<1时,GPC优化算法则不启动,底层回路就相当于普通的PID控制器;
(2)当hr≥1时就认为系统的状况发生了改变,将启动上层优化,此时需要重新整定PID的控制参数,同时将控制量的变化及变化率约束在系统可控制与执行的范围内。改进的GPC-PID控制算法流程图3所示。
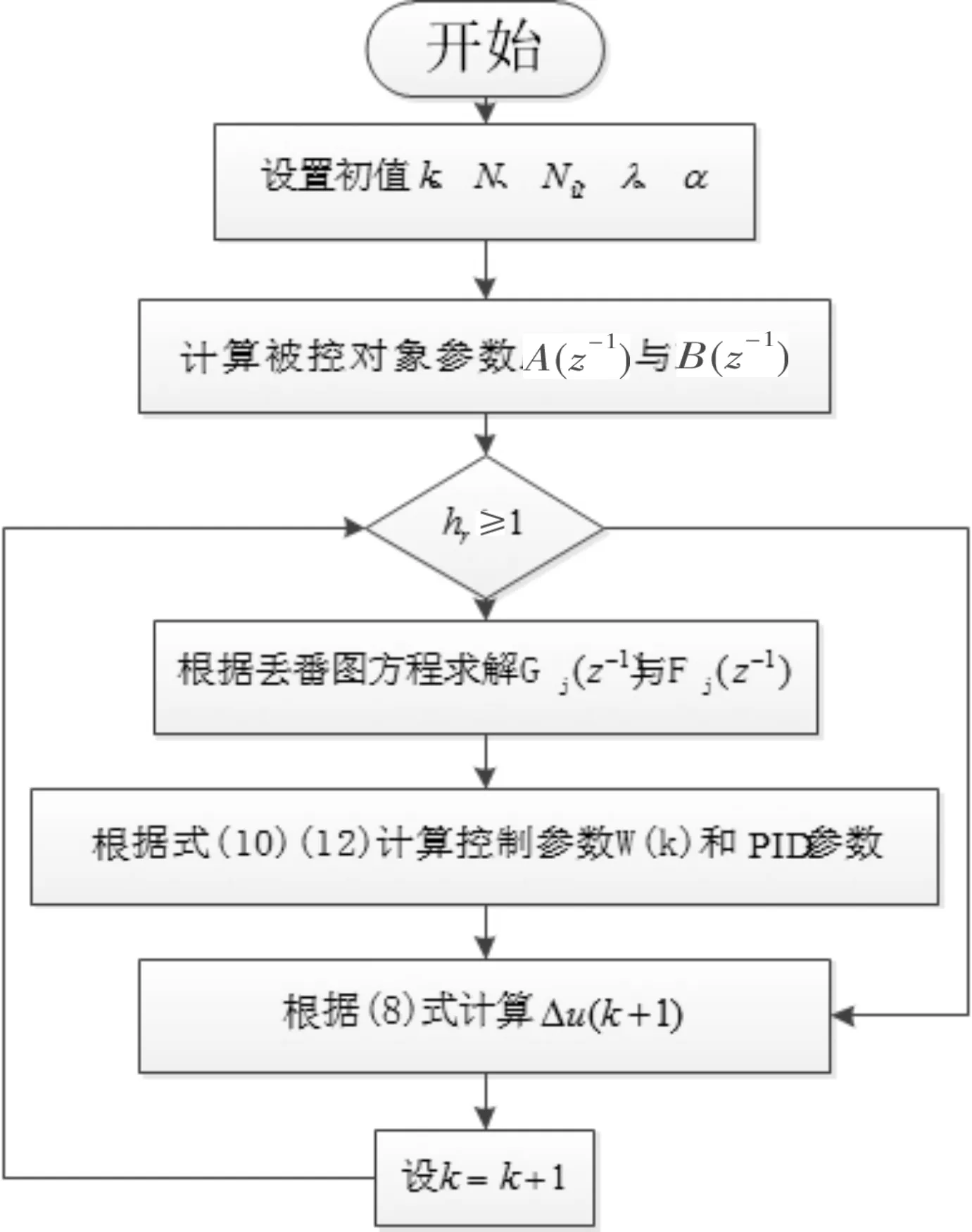
图3 控制算法流程图
4 实验仿真及结果分析
本文以某污水处理厂的单变量模型作为被控对象,其传递函数为G(s)=0.004/(300s+1)e-6,设定将生化反应池好氧区的溶解氧浓度控制为2.0 mg/L。其中控制器参数为运用相同的控制参数,普通PID算法与改进GPC-PID算法的仿真结果如图4所示。

图4 控制输出
其中,传统PID算法的曲线峰值较高,而改进GPC-PID算法的曲线峰值较低。改进GPC-PID算法比传统PID控制算法所用的时间更短,被控量能更快地达到稳定状态。改进GPC-PID算法较好地实现了这样的特性,节省了在线整定参数计算的时间,而原算法没有这样的优点。
如表1所示,改进GPC-PID算法优化过程中使用时间更短,而且系统输出的超调量显著降低。改进算法在线优化计算时间更短,较大程度减少了在线反复求解Diophantine方程的求解次数和复杂度,减少了系统的运算量。最终得到的曲线也比较平滑,达到了预想的效果。

表1 算法在线计算时间
5 结束语
在确保传统PID控制性能与简单易实现等特点的基础上,根据GPC算法原理在线整定PID控制参数。改进后的算法减少了方程的求解次数和复杂度,降低了系统的运算量,提高了算法的运行速度,在某种程度上扩大了算法解决相关问题的应用范围。
[1] Zhang P, Yuan M Z. Study on dissolve oxygen control method based on international evaluation benchmark[J].Information and Control,2007,36(2):199-203.
[2] 项雷军,张学阳,郑力新,等.污水处理系统溶解氧的区间预测控制方法[J].计算机与应用化学, 2015,32(4):468-472.
[3] 魏伟,王蒙,刘载文,等. 基于活性污泥法的污水处理线性自抗扰控制[J].计算机仿真, 2015, 32(8):417-421.
[4] 张学阳,项雷军,林文辉,等. 神经网络预测控制在污水处理溶解氧控制中的应用[J].华侨大学学报:自然科学版, 2015(3):280-285.
[5] 席裕庚.预测控制[M].北京:国防工业出版社,1993.
[6] 李少远.全局工况系统预测控制及其应用[M].北京:科学出版社, 2008.
[7] 王松桂,杨振海.广义逆矩阵及其应用[M].北京:北京工业大学出版社,1996.
[8] 张昊.污水处理系统中加药控制算法的研究[C].通化:全国冶金自动化信息网2016年会论文集,2016.
[9] Jiang N, Liu X, Li S, et al. Dual-rate sampled systems PID type generalized predictive control[J]. Journal of Computational Information Systems, 2012, 8(17):6995-7002.
[10] Li X, Fang Y, Zhang R. Hierarchical GPC-based PID control strategy for SST of USC under variable loads[J]. International Journal of Control & Automation, 2015(8):2317-2326.
Improved GPC-PID Control Algorithm for Dissolved Oxygen In Wastewater Treatment System
LIU Xiang,ZHAO Min
(School of Optical-Electronic Information and Computer Engineering,University of Shanghai for Science and Technology,Shanghai 200093,China)
aiming at the problem that the real-time change of dissolved oxygen (do)concentration is difficult to control in the wastewater treatment process, a do value control algorithm based on improved gpc-pid is proposed. by improving the rolling optimization principle of gpc-pid algorithm, the system can adjust the pid parameters online, and no need to solve the diophantine equation again and again when the concentration of dissolved oxygen is stable. the improved algorithm reduces the time and complexity of solving the equations, reduces the computation of the system, and solves the control problems caused by time delay. the simulation results show that the improved gpc-pid predictive control algorithm can get better control effect, and improve the stability of the system and the fast calculation of the optimization.
dissolved oxygen concentration; wastewater treatment; predictive control; generalized predictive control pid
2016- 05- 15
刘向(1990-),男,硕士研究生。研究方向:预测控制。
10.16180/j.cnki.issn1007-7820.2017.01.024
TP311;X52
A
1007-7820(2017)01-087-04
