基于四元数解算和模糊PID控制的四轴旋翼机
2017-03-29夏纪冬刘子龙张文文
夏纪冬,刘子龙,张文文
(上海理工大学 光电信息与计算机工程学院,上海 200093)
基于四元数解算和模糊PID控制的四轴旋翼机
夏纪冬,刘子龙,张文文
(上海理工大学 光电信息与计算机工程学院,上海 200093)
针对四轴旋翼机在运动过程中不能较好地保持稳定飞行姿态的问题,系统采用四元数算法对测量磁力传感器造成的常值漂移误差进行校正,采用模糊PID控制算法来调整系统运动姿态,运用Matlab Simulink对Fuzzy PID控制算法进行仿真。实验结果表明,四轴旋翼机控制系统的超调量为6.0%<20%,稳态误差为0.01,具有较好的抗干扰性。在实际飞行测试中,地面站接收的数据显示模糊PID控制具有较好的控制性能。
STM32F407;四元数;模糊PID控制;四轴旋翼机
四轴飞行器是一种具有对称结构的多旋翼直升机,由固定在中心板上的4 个安装了旋翼的悬臂组成[1]。其能够提供稳定的特技飞行,以其形体小、成本低、低环境要求、较强生存能力、省人、省物、安全方便等优势,以及广泛的实用价值,成为航模爱好者和科研人员研究的热点和对象[2]。运用集成电路技术,能够使四轴飞行器共享电路板、电池等,设计出精简紧凑的整体四轴旋翼机结构,高效的利用旋翼机产生的升力,实现旋翼机稳定的飞行姿态,以便将四轴旋翼机更广泛的应用于工业和农业领域中[3-5]。
1 飞控系统的结构分析和硬件设计
1.1 飞控系统运动结构
四轴飞行器的飞行状态由螺旋桨拉力的大小和螺旋桨盘的方向决定[6-7]。其有4个螺旋桨,所以可通过调节4个无刷电机的转速和方向,来实现四轴旋翼机的姿态控制,包括翻转、俯仰、偏行等[8-9]。
1.2 部分硬件姿态传感器设计
主控制器使用ARMv7m架构的STM32F407芯片,时钟频率可达168 MHz(可获得210DMIPS的处理能力),主要责读取接受模块的飞行命令信息和姿态传感器收集到的信息,将得到两个信息进行解算,经过四元数解算和PID模糊控制运算,得到飞行控制信号量,通过PWM方式来驱动4个无刷电机的转速和方向[10-11]。
姿态传感器采用MPU6050,内部含有第二个I2C 接口,可与外部磁力传感器AK8975三轴罗盘连接,同时利用芯片内部的DMP,选择I2C 接口通道,输出比较完整的9轴融合姿态演算数据。有了 DMP,可使用 InvenSense 公司提供的运动处理函数资料库,实现姿态解算, 减少了运动处理运算对整个飞控操作系统的负荷,降低了项目开发难度,MPU6050硬件电路设计如图1所示。
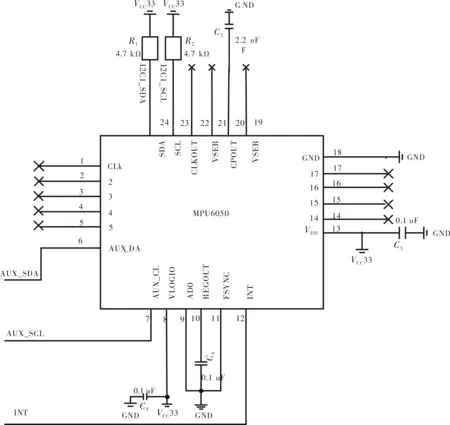
图1 MPU6050硬件电路设计
MPU6050的I2C的SCL和SDA的输出端可分别连接一个上拉电阻R1(4.7 kΩ)、R2(4.7 kΩ)。 CPOUT引脚需先接旁路电容C2(22 μF),然后接GND。引脚REGOUT主要是校准滤波电容,可先接0.1 μF的滤波电容,然后接地。因本飞控系统中使用的是内部时钟,故CLK引脚可以选择悬空,此外MPU6050的AUX_SCL和AUX_SDA分别连接AK8975三轴罗盘的AUX_SCL和AUX_SDA,AK8975三轴罗盘的应用电路设计如图 2所示。

图2 AK8975三轴罗盘应用电路
此外AK8975只需CSB和VID引脚之间连接一个0.1 μF的电容,VDD接3.3 V的电压,CAD0、CAD1、VSS引脚接直接接地外,其他引脚选择悬空。同时采用MS5611高精度气压计应用于高度检测,应用电路设计如图 3所示。

图3 高精度气压计应用电路设计
高度检测芯片MS5611通过I2C1_SCL和I2C1_SDA 分别和 F407芯片的I2C1_SCL和I2C1_SDA相连,并且F407芯片的I2C1_SCL和I2C1_SDA分别连接一个4.7 kΩ的上拉电阻。
2 系统的四元数算法和模糊PID算法
2.1 四元数算法及其C语言实现
在本系统MPU6050等磁力传感器大部分误差的是由于常值漂移造成的,为减少误差对测量角速度的影响,采用四元数对常值漂移进行校正。将得到的加速度的数值与磁场的值进行校正,由叉积公式得
ex=(azre×ay-ayre×az)+(mzre×my-myre×mz)
(1)
ey=(axre×az-azre×ax)+(mxre×mz-mzre×mx)
(2)
ez=(ayre×ax-axre×ay)+(myre×mx-mxre×my)
(3)
式(1)~式(3)中,ex、ey、ez为叉积的和;exre、eyre、ezre为加速度标准矢量;ax、ay、az为加速度测量矢量;mxre、myre、mzre为磁场标准矢量;mx、my、mz为磁场的测量矢量。
由式(1)~式(3)得角速度ω漂移修正值为
(4)
式(4)的wx(i)、wy(i)、wz(i)是角速度;KP为比例系数;KI为积分系数。将修正后的w通过代入式(5)
(5)
式(5)中,H(i+1)=[p0,p1,p2,p3]T,p0,p1,p2,p3为四元数;I是单位向量;T是更新周期。
Δθ2=[wx(i)×T]2+[wy(i)×T]2+[wz(i)×T]2
(6)
(7)
由式(1)~式(7)得欧拉角为
(8)
式(8)中,的ψ为航向角;φ为横滚角;γ为俯仰角。
本设计采用的软件开发工具是Keil公司开发的最新MDK5开发平台,软件功能强大,软件平台集编译连接器、库函数以及仿真调试器为一体,缩短了设计周期。四元数算法在C代码中的部分实现如图4 所示。

图4 四元数算法在C语言上的实现
2.2 模糊PID控制及其仿真
经典PID控制原理简单、稳定性好,广泛的应用于工业过程控制中[12]。其性能的品质在于调节过程中对PID各参数值,但对于复杂的、多变的、非线性控制领域具有一定的局限性,为满足对复杂多样的控制要求,系统采用模糊PID控制[13-14]。模糊控制是将工程技术人员实践所获得的经验理论和知识转化为控制规则和策略,模糊PID控制具有经典PID控制的优势,又兼有复杂控制的优势,因此在实际中拥有广泛的应用价值[15]。
考虑四轴旋翼机姿态控制的复杂性,同时考虑到P比例参数、I积分参数、D微分参数的相互作用和联系,先计算飞控系统误差e及误差的变化率ev,然后将e和ev作为PID自整定的输入,使用一定的控制规则在线对PID控制参数进行调整修改。FUZZY-PID控制结构图,如图5所示。

图5 FUZZY-PID结构图
通过模糊控制规则将控制输入转化为控制输出,目的是将输入的确定量转化为模糊矢量,飞控系统的误差e以及ev在模糊集上的取值范围e,ev={-1,0,1}模糊子集的取值范围e,ev={P,N,Z},P,N,Z分别代表正值,0值和负值。
如图6所示,在Simulink仿真下输入一定的值,在一定的模糊规则控制下,通过调整系统误差e和误差变化率ev便可通过模糊控制器得到PID调节相对应的修正参数值。

图6 基于模糊PID的控制模型

图7 FUZZY-PID模型仿真结果
在姿态稳定实现上,采用模糊PID算法,能实现良好的姿态控制,既使控制系统的模型选取不是特别好,其也可进行校准,Matlab模拟软件提供了一个良好的平台,便于了解该系统的控制参数的影响。然而,一个实际的机载系统使用该软件获得的参数进行调试,四轴旋翼机系统并不能够稳定运行。这是由于构建了并不准确的实际四旋翼系统的数学型造成的,因此还需在此基础上进行PID实际参数的调试。
3 系统软件设计以及飞行调试
在四轴旋翼机控制系统中,软件设计主要有:四元数姿态解算算法,模糊PID姿态控制算法,超声波定高算法,速度检测,电压电流检测等。在实际飞行调试过程中,相比经典PID控制,加入模糊控制算法,通过对模糊控制PID参数的反复实验,控制品质得到了大幅提高,四轴旋翼机的稳定姿态得到了良好的实现。
在实际飞行中,通过数传模块将四轴旋翼机的空中飞行姿态实时传递给上位机,如图8所示。可以观察到各个电机输出的相对大小,三轴加速度计和陀螺仪数据,以及气压高度、电压电流等数据,以便对四轴旋翼机的控制效果以及飞行姿态有更好的了解和改进。
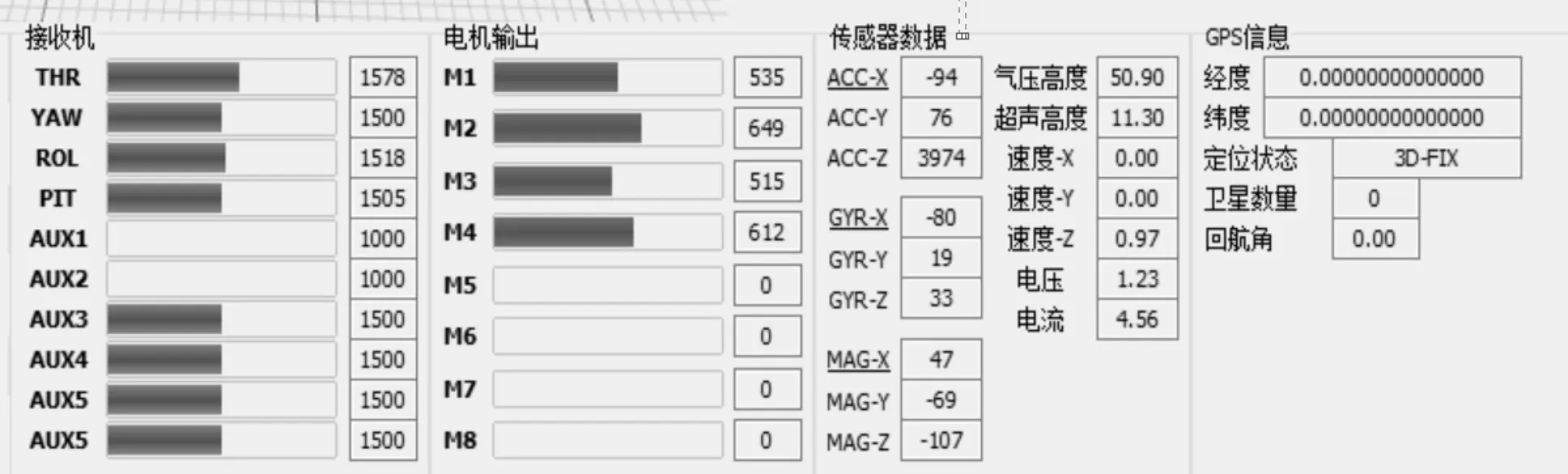
图8 上位机接受部分数据图
4 结束语
经对硬件平台的实际调试,四元数算法对MPU6050等姿态传感器造成的常值误差具有显著的调节作用,模糊PID算法能使四轴飞行器保持较稳定的飞行姿态和悬停,后续还需要继续优化控制算法,增加一些GPS定位和航拍功能,针对电池供电时间短的问题,将考虑设计用太阳能电池板或者无线充电模块给四轴飞行器供电。
[1] 刘焕晔.小型四旋翼飞行器飞行控制系统研究与设计[D].上海:上海交通大学,2009.
[2] 夏路.无人机编队导航与控制系统研究[D].哈尔滨:哈尔滨工业大学,2014.
[3] 袁征,罗卫兵,武毅.基于RSSI的微小型无人机天线自动跟踪系统设计[J].飞航导弹,2015(8):25-28.
[4] 贺天鹏,李书,李小龙.直升机旋翼/机体动稳定性研究进展[J].力学与实践,2013,35(3):1-19.
[5] 孙骅.基于GPS与AHRS的四轴飞行器悬停算法研究[J].机械科学与技术,2013,32(4):481-487.
[6] 史晓宁.飞行机器人轨迹跟踪控制的几何方法研究[D].哈尔滨:哈尔滨工业大学,2013.
[7] 吴怀宇,周兆英,熊沈蜀,等.微型飞行器的研究现状及其关键技术[J].武汉科技大学学报:自然科学版,2000,23(2):170-174.
[8] 郑权,忻尚芝,钱建秋.基于改进遗传算法的PID参数研究[J].电子科技,2015,28(11):5-7.
[9] 邓博文,窦强,龚国辉,等.四旋翼飞行器悬停算法设计与实现[J].电子科技,2015, 28(11):21-24.
[10] 刘杰.四轴飞行器研究与设计[D].南京:南京邮电大学,2013.
[11] 万俊.四轴飞行器的研究与制作[D].武汉:华中师范大学,2014.
[12] 黄宜庆.PID控制器参数整定及其应用研究[D].淮南:安徽理工大学,2009.
[13] 齐琳.模糊PID动态切换控制算法的研究[D].北京:北京交通大学,2008.
[14] 丁杭成.船舶航向智能PID控制算法研究[D].大连:大连海事大学,2010.
[15] 陆华颖,程光伟,陈凯.模糊PID双闭环直流电机调速系统仿真[J].电子科技,2011,24(10):56-58.
Four Elements Calculation & Fuzzy PID for Controlling Four Axis Aircraft
XIA Jidong,LIU Zilong,ZHANG Wenwen
(School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology, Shanghai 200093, China)
For four axis aircraft machine can’t be better to maintain stable flight attitude in motion process. This system uses quaternion algorithm to correct the error related to the measurement of the magnetic sensor, using the fuzzy PID control method to adjust the attitude of the system movement.Using MATLAB Simulink to test the effect of the puzzy PID control method, and the overshoot of the four axis aircraft machine control system is 6.9 percent less than 20 percent, steady-state error is 0.01, The ground station received data show that the fuzzy PID method has good effect in flying.
STM32F407; four element number; fuzzy PID control; four axis rotor machine
2016- 05- 09
国家自然科学基金资助项目(61573246)
夏纪冬(1989-),男,硕士研究生。研究方向:控制理论与控制工程等。
10.16180/j.cnki.issn1007-7820.2017.01.020
TP391.9;V249
A
1007-7820(2017)01-072-04
