基于全变分模型改进的图像修复算法应用
2017-03-29谢正伟王创新
谢正伟,王创新
(长沙理工大学 电气与信息工程学院,湖南 长沙 410004)
基于全变分模型改进的图像修复算法应用
谢正伟,王创新
(长沙理工大学 电气与信息工程学院,湖南 长沙 410004)
传统全变分(TV)模型对非纹理破损图像有较好的修复效果,但TV算法对参数敏感,导致修复图像容易在平滑区域产生阶梯效应。文中在传统TV模型的基础上,结合非线性扩散的思想,提出了一种针对参数的自适应迭代函数图像修复算法。实验结果表明,该算法在修复过程中扩散系数和自适应迭代函数的共同作用,消除了阶梯效应;修复的图像自然过渡,边缘信息保存良好。
TV模型;图像修复;非线性扩散;自适应
图像修复[1-2]是数字图像处理的一个分支。是利用已破损的图像信息,使图像破损部分还原并修复。图像修复技术分为两大类:一类是基于纹理的图像修复算法[4],该算法包含基于图像分解的采样纹理合成的修复技术和基于块思想的纹理图像修复技术;另一类是非纹理图像修复技术即基于偏微分数理方程(PDE)修复算法,PDE算法的图像修复是一个非适定(病态)问题[5]。为使修复后的图像人眼看起来“自然”,文献[6]中,提出了PDE图像修复算法的3准则:局域性、边缘连通性和去噪的鲁棒性。具有代表性的偏微分图像修复算法 有曲率驱动扩散(CDD)修复算法[7-8]、BSBC修复算法[9]、全变分(TV)修复算法[10]。这类算法将PDE进行数值化并进行差分转换,最后通过迭代求解偏微分方程。
Chan[6]等将TV去噪复原算法进行扩展,将TV算法运用到图像修复中。因此基于TV模型的图像修复算法成为近年来研究的热点。由于算法对参数的敏感和运算量较大,提出了一个针对参数的自适应迭代函数,并结合了非线性的思想,使得改进后的算法加快了图像的修复速度并具有良好的鲁棒性。
1 图像修复的TV算法
2002年Chan等人基于TV去噪模型的拓展,提出图像修复的TV模型即破损图像的修复也是一个最小化能量泛函问题。在图像I的领域内,Φ为图像破损领域,Ω为图像破损领域的外邻域,Φ∪Ω为修复后的领域;且破损图像的边界一般具有连通性,如图1所示。

图1 破损区及邻域示意图
则基于TV模型的图像修复代价函数为

(1)
式中,I0是初始图像;为梯度算子;λ为拉格朗日乘子;|I|dxdy为图像修复的TV模型,保证需要修复图像尽可能的平滑;|I-I0|2dxdy=const为有约束的最小二乘法,保证修复后的图像具有良好的稳定性。
当求解minEλ(I)时,得式(1)的Euler-Lagrange方程
(2)

由于式(2)是一个静态偏微分方程,其求解比较困难。因此才要采用梯度下降流的方法将求解静态非线性PDE转换动态PDE,当迭代达到稳态时的解就是式(2)的解,则式(2)对应的梯度下降流方程为
(3)
其中,a是一个较小的常量;为避免梯度模值|I|为0。
2 非线性扩散方程
为达到去噪并同时保护边缘,Perona和Malik[9]提出了非线性扩散PDE方程
(4)
式(4)中,g(|I|)是与图像梯度模值有关的扩散系数;g(|I|)是一个满足g(0)=1,g(∞)=0的单调递减有界函数。图像处于边缘时|I|较大,g(|I|)较小图像扩散程度小; 图像处于平滑区域时|I|较小,g(|I|)较大加快了图像在平滑区的扩散。文献[11~12]给出的扩散系数函数分别为如式(5)和式(6) 所示。
g1(|
(5)
g2(|
(6)
式(5)和式(6)中的正常数K是调整保护梯度的范围,扩散系数函数g(|I|)与图像梯度模值|I|的关系如图2所示。
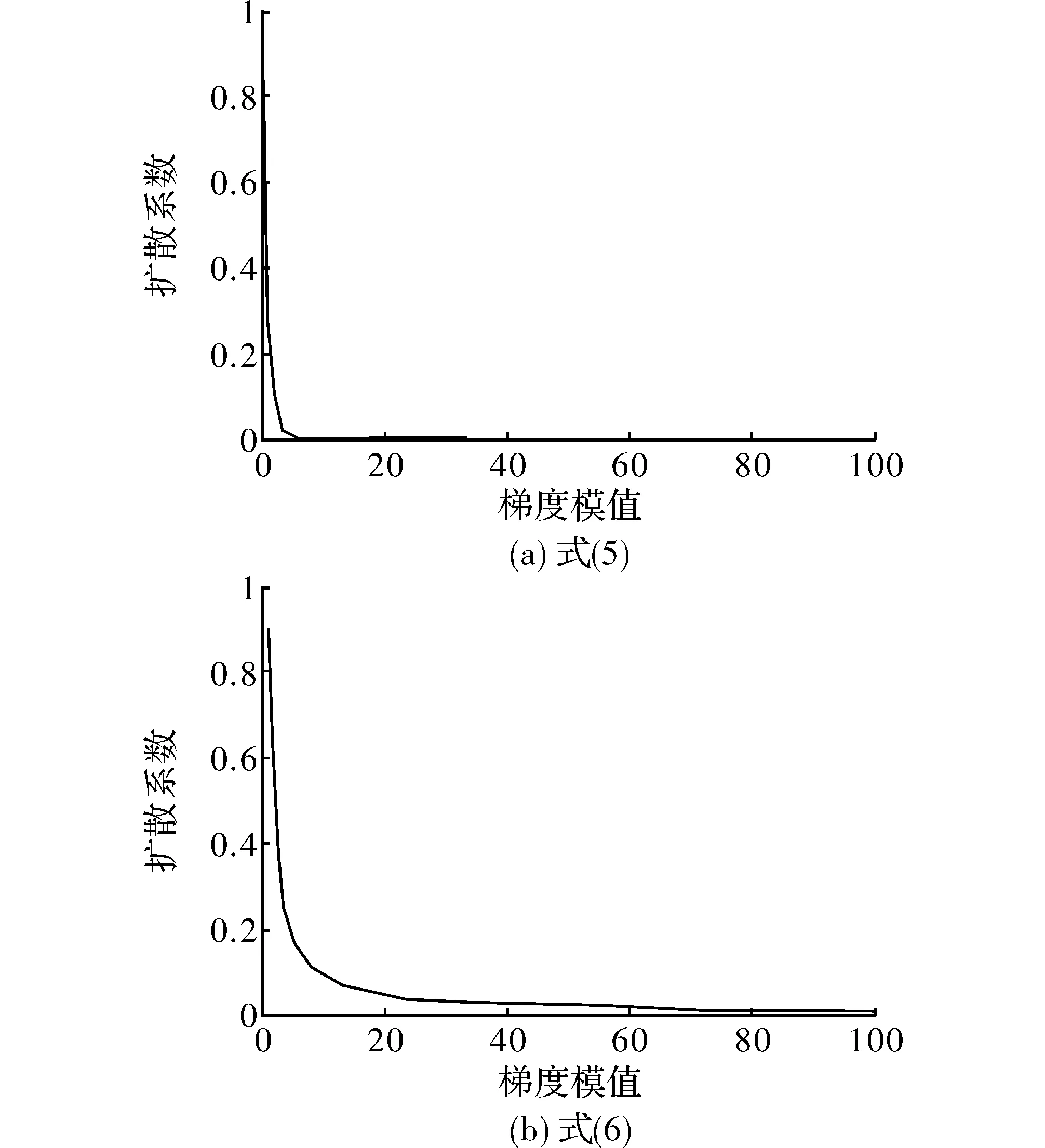
图2 扩散系数和梯度模值的关系
对破损图像,图像在破损区存在梯度模值较大的区域,图2(a)中g(|I|)在|I|较大时,扩散系数为0,因此在较大梯度模值的点的扩散就会停止。而图2(b)中,在对应较大的梯度模值时扩散系数仍>0,加强了图像破损区的扩散速度;因此本文扩散系数函数选g2(|I|)。
3 TV模型改进及数值实现
3.1 改进的修复算法
传统的TV图像修复模型为各向异性扩散。也就是说TV算法无论在大梯度还是在小梯度,对修复区域的领域像素点采用相同的扩散系数进行修复,因此易在平滑区产生阶梯效应;且式(3)中的参数a,在图像修复区域,a的参数的选取对图像的修复效果和修复速度影响大;若a取值较大,|I|的作用弱,可知迭代的得到的修复图像等效各向同性扩散,加快了迭代效率和扩散速度;若a取值很小,|ΔI|的作用强,得到修复的迭代图像为各向异性扩散,突出了图像的边缘。

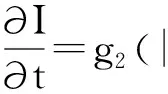
(7)
3.2 数值实现
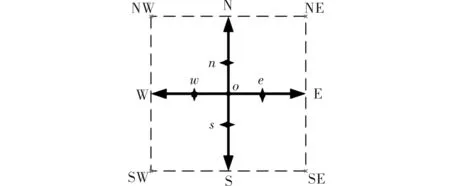
图3 邻域像素点
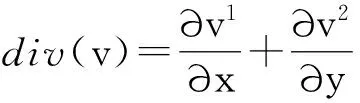
(8)
式(8)中,h为步长,“半点”离散化时为1。选取n半像素点,其中I0为修复后的图像

(9)
|In|≅
(10)
将式(8)~式(10)代入式(7)得到离散化的修复方程
(11)
(x,y)∈Ω
(12)
整理式(11)和式(12),并采用Gauss-Jacobi迭代算法[15],目标像素o点为破损像素点,则(x0,y0)∈Φ,在破损区域λ(o)=0,得到迭代次数为n0的图像修复区域数值方程
(13)
4 实验结果分析与对比
本实验在CPU为3.33 GHz,内存为2 GB的计算机平台,运用Matlab7对算法进行对比验证。本文实验采用Lena灰度图像,像素大小为256×256;进行两组对比实验,验证本文算法。对比实验1,是对Lena图像进行划痕修复,对比实验结果如图4所示。对比实验2,是对Lena图像进行文字修复,对比实验结果如图5所示。根据文献[15],当自适应参数a为0.01时,为停止迭代阈值。因此,本文的两组对比实验根据式(13)的迭代方程,当修复迭代次数达到2 000次或自适应参数a的阈值为0.01时停止迭代,即得到修复图像。

图4 划痕修复实验

图5 文字修复实验
在图4(d)~图4(e)和图5 (d)~图5(e)中,采用TV算法和自适应算法输出的修复图像有明显的阶梯效应;图4和图5(g)可看出,本文算法对划痕修复和文字修复输出图像无明显的阶梯效应,从使修复的图像边缘清晰,过渡自然。且基于偏微分的图像修复采用峰值信噪比(PSNR)[8]来对修复的结果进行评价。评价函数如下
(14)
式(14)中,M×N为图像的像素;I(i,j)为修复后的图像。修复效果越好,PSNR值也越大;修复后的PNSR值及算法的迭代时间如表1和表2所示。

表1 划痕修复实验

表2 文字修复实验
从表1和表2可知,本文算法相比TV算法和自适应算法,PSNR值有大幅提高;相比于复杂的CDD算法,在基本相同的修复效果下,修复图像所耗费的时间要少,且本文算法输出的修复图像,无明显的阶梯效应,体现了本文算法的有效性和实用性。
5 结束语
本文通过分析和评价TV图像修复算法的局限性,提出了一个针对参数 的自适应迭代函数并结合非线性扩散的思想,对TV算法进行改进。实验结果表明,改进后的算法复原的图像,峰值信噪比得到较大提高,修复效果自然,验证了本文算法的可行性。
[1] 张红英,彭启琮.数字图像修复技术综述[J].中国图象图形学报,2007,12(1):1-10.
[2] 赵颜伟,李象霖.一种基于TV模型的快速图像修复算法[J].微电子学与计算机,2009,26(6):253-256.
[3] 邵肖伟,刘政凯,宋璧.一种基于TV模型的自适应图像修复算法[J]. 电路与系统学报,2004(2):113-117.
[4] 朱晓临,许云云,李震宇.自适应Snake-TV模型在彩色图像修复中的应用[J].合肥工业大学学报:自然科学版,2011, 34(11):1655-1660.
[5] 林云莉.数字图像修复算法的研究[D].广州:华南理工大学,2010.
[6] Chan T F,Shen J.Mathematical model for local non-texture inpaintings[J].SIAM Journal on Application Mathmatical,2002,62(3):1019-1043.
[7] Tony F Chan.Nontexture inpainting by curvature-driven diffusions[J].Journal of Visual Communication and image Representation,2001,12(19):436-449.
[8] 印勇,李丁,胡琳昀.采用CDD模型的自适应图像修复算法[J].重庆大学学报,2013,36(4):80-86.
[9] Perona P,Malik J.Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.
[10] 林云莉,赵俊红,朱学峰,等.改进的模型图像修复算法[J].计算机工程与设计,2010,31(4):776-779.
[11] 王涛,王军峰,白青,等.改进的TV模型图像修复算法[J].计算机系统应用,2013,22(3):121-124.
[12] 田艳艳,祝轩,彭进业,等.一种基于整体变分的图像修补算法及其应用[J].计算机工程与应用,2008,44(26):180-182.
[13] 王大凯,候榆青,彭进业.图像处理的偏微分方程方法[M].北京:科学出版社,2008.
[14] 顾建平.图像修复快速算法研究[D].北京:中国科学院自动化研究所,2005.
[15] 屈磊,韦穗,梁栋,等.综合自适应与多尺度的TV图像修复方法[J].计算机工程,2007,33(22):18-20.
Application of Improved Inpainting Algorithm Based on TV Model
XIE Zhengwei,WANG Chuangxin
(School of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410004, China)
The Total Variation (TV) has a positive effect for non-texture damaged image; Owning to the TV algorithm of parameter sensitivity, the result of inpainting is easy to occur staircase effect. This paper proposes an improved image inpainting algorithm based on TV model, with the nonlinear diffusion theory and an adaptive iterative function for the parameter; In consequence of the influence of diffusion coefficient and an adaptive iterative function, the improved algorithm eliminate the staircase effect. The consequence of image inpainting transit naturally and protect the edge information.
TV model; image inpainting; nonlinear diffusion; self-adaptive
2016- 03- 24
谢正伟(1991-),男,硕士研究生。研究方向:图像处理。王创新(1965-),女,副教授,硕士生导师。研究方向:图像处理等。
10.16180/j.cnki.issn1007-7820.2017.01.017
TP391.41
A
1007-7820(2017)01-061-05
