一种新型1+D变换器的非线性及其控制技术

李少龙，周 敏，崔 悦，巫思源，卢浩孙，陈健霖

(上海理工大学 光电信息与计算机工程学院，上海 200093)

一种新型1+D变换器的非线性及其控制技术

李少龙，周 敏，崔 悦，巫思源，卢浩孙，陈健霖

(上海理工大学 光电信息与计算机工程学院，上海 200093)

针对部分便携式设备中升压变换器输出电压谐波不理想的情况，提出了一种新型的1+D非隔离式变换器，并对该拓扑结构非线性行为了进行分析研究。为控制其混沌行为采用了基于时间连续延迟反馈方法的混沌控制技术，通过搭建Simplorer仿真模型获得仿真结果，验证了在该变换器闭环系统中采用延迟反馈控制策略可有效抑制其混沌现象，同时使负载瞬态响应得到改善。

1+D非隔离式变换器；混沌控制技术；Simplorer仿真

放大电路等设备通常需要较高的供电电压来满足自身供电需求和足够的电压放大比例，因此当低压电源常作为供电电源时，需通过变换器进行升压。目前，在众多3C电子设备中，通常需要变换器来提升一个较低或更低的电压，尤其是针对一些便携式设备，例如MP3播放器、蓝牙设备、个人电子助手等。对于这类需求，考虑输出电压的谐波就显得尤为重要。就传统的非隔离式升压变换器如Boost变换器和Buck-Boost变换器，他们的输出电流有波动[1-2]，这就导致输出电压谐波很大。为了克服这一问题，一个方法就是使用大电容和低等效电阻，另一个方法是增加电感电容滤波[3]，此外还有增大开关频率的方法等[4]。近期，一些电压谐波较小的升压变换器技术被提出，如双向Buck-Boost变换器的交错控制。在提升输出电压的同时能减小输出电压的谐波。然而在这些变换器控制中，电路工作在电感电流连续模式下时，均会有一个零点在左半平面，相比于Buck电路，要获得好的负载瞬态响应大都比较困难[5]。

基于以上原因，本文提出了一种新型的1+D升压变换器，该变换器总能工作在电感电流连续的状态下。除此之外，输出电流无波动，减小了电压谐波。其表现类似于带有同步整流的Buck变换器。该变换器拥有较好的负载瞬态响应，且电压比(输入比输出)不同于传统的变换器，其比值为1+D，其中，D为PWM控制方波的占空比。

1 1+D变换器的拓扑结构及其工作原理

图1 新型1+D变换器的闭环拓扑结构

该变化器电路可工作在两种模式下，并通过这两种模式的交替运行，可达到变换输入输出电压，同时使电流工作在连续状态下的目的。

模式1 如图2所示，S1导通，S2关断，电感上的压降为输入电压和Cb上的电压之和减去输出电压，流过电容C的电流，为流过电感L的电流减去负载电流，在Mode 1下，Cb放电， 储能电感充磁。

图2 1+D变换器工作模式1

因此，此时系统响应等式如下

(1)

模式2 如图3所示，S1关断，S2导通，电感L上的压降为输入电压减去输出电压，与此同时，流过电容C的电流为流过电感L电流减去负载电流。除此之外，在模式2中，电源为Cb充电，储能电感放磁。

图3 1+D变换器模式2

因此，系统此时的响应等式如下

(2)

根据伏秒法则，电路在一个稳定状态下，ΔION=ΔIOFF=ΔI，也就是说电路处于稳定状态下，加在电感两端的电压在开关导通时刻的值与导通时间相乘，等于电感电压在开关关断时刻的值乘以关断时间[2]，其表达式如下

VON×tON×VOFF×tOFF

(3)

电感上的电压及持续时间的乘积为伏秒数，上式表示处于稳定状态的电感，开关到同时间(电流上升段)的伏秒数须与开关关断(电流下降段)时的伏秒数在数值上相等，尽管两者符号相反。只对电感电流连续模式(CCM，Continuous Current Mode)进行讨论，此时

T=TON+TOFF

(4)

可做如下推导，电流上升阶段

电流下降阶段

根据伏秒法则，由式(3)和式(4)可得该拓扑结构的输出比输入的电压转换比为

(5)

2 1+D变换器的非线性现象研究

构建合适的1+D变换器系统仿真模型是研究其非线性动力学行为的基础，根据峰值电流控制1+D变换器原理，基于Simplorer仿真软件搭建的系统模型如图4所示。有关峰值电流控制的1+D变换器的动力学研究，通过分岔分析可揭示峰值电流控制的1+D变换器的复杂动力学行为，能对其进行工作状态的域估计；稳定性分析可明确峰值电流控制1+D变换器的分岔路径，从而能够对其进行稳定参数的域估计[6-7]。

输入电压Vi=24 V，以参考电流Iref为混沌变量，通过Simplorer仿真模型可得到峰值电流控制模式下, 1+D变换器主要参数变化时电感电流波形图及电感电流与电容电压的相位图。当Iref=4 A时Simplorer仿真结果如图5所示。图中电感电流iL与电容电压vC相位图显示了双周期回路轨迹特征。 当Iref=6 A时仿真结果如图6所示，iL与vC相图仿真结论符合单周期轨道的特征。而在Iref=8 A时系统进入混沌状态，此时电感电流与电容电压的值呈现出无规则状态。

图4 峰值电流模式下的 变换器

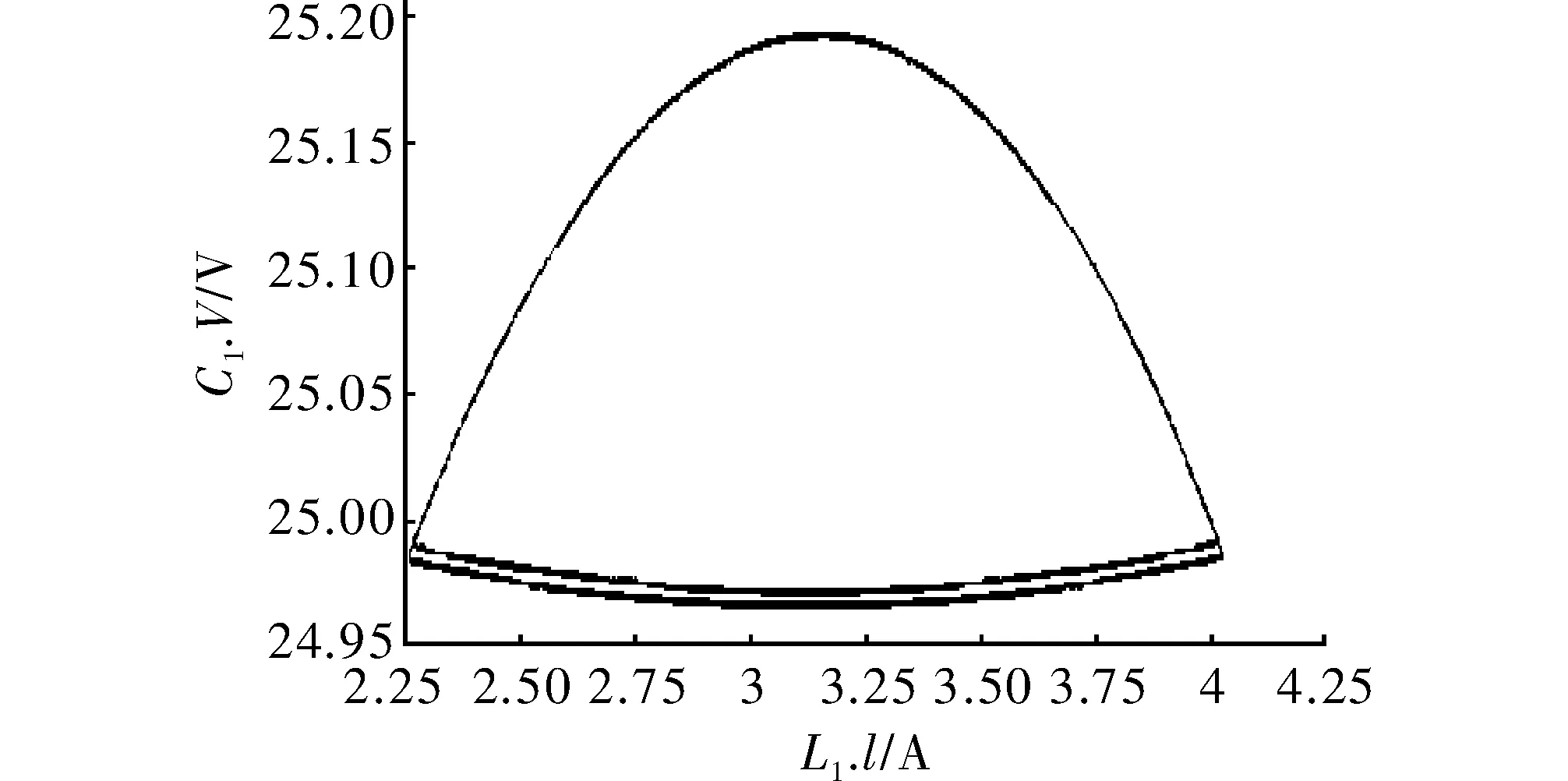
图5 Iref=4 A时电容电压vC、电感电流iL相位图

图6 Iref=6 A时电容电压vC、电感电流iL相位图

图7 Iref=8 A时电容电压vC、电感电流iL相位图

3 变换器的非线性控制策略

开关变换器的混沌控制技术主要采用两种方法，即反馈控制策略和非反馈控制策略[8-9]。前者的特点是保持了系统原有的动力学性质，且无需要大的控制信号。混沌运动具有遍历性，所以系统在某一时刻总会运行至目标态附近，以此为基础设计的反馈控制能确保目标态的局域稳定性[10-11]。而后者非反馈控制方法则需要外加信号干预系统，比较有灵活性具有易于实现的特点，但是应用上也具有一定的局限性[12-13]。本文所研究的斜坡补偿法属于反馈混沌控制方法[14]。

该方法是基于时间连续延迟反馈的想法，小微扰计算在高采样率，不改变所需的不稳定周期轨道的形式,但在一定条件下可稳定[15-16]。反馈控制F(t)等于当前值y(t)及其τ秒之前值的差值乘以一个常数K

(6)

F(y,t)=K[y(t-τ)-y(t)]

(7)

其中，K是反馈强度。

图8 变换器延迟反馈控制仿真电路

图9 Vi=24 V时采用延迟反馈输出电压vC和电感电流iL相位图

通过将图9与图5～图7对比可知，在相同情况下加入混沌控制时，可明显地观察到延迟反馈控制的加入使系统避免了进入混沌状态，效果明显。使用该方法可消除混沌中存在的混沌吸引子，而正是因吸引子的存在才导致了系统由稳定进入不稳定周期轨道。基于反馈参数τ、K研究混沌控制，能适应于1+D变换器的情况。

4 结束语

本文提出了一种新型的1+D变换器，其通过在两种模式下交替切换，达到对输入电压进行升压变换。通过原理分析可知，该变换器可保证电流工作在连续状态下，且输出电压的谐波较小。然后，通过对其非线性的研究，发现该拓扑结构中同样存在混沌行为，进而提出了一种基于延迟反馈控制策略的混沌控制技术。并通过仿真Simplorer软件建模和仿真，验证了该算法可有效抑制变换器的混沌行为。使基于该变换器的闭环系统获得较好的工作性能和较稳定的工作状态。

[1] Peng X, Ren Y C,Mao Y,et al.A family of novel interleaved DC/DC converters for low-voltage high-current voltage regulator module applications[J].IEEE Transactions on Circuit System: Fundam Theory Application, 1992, 39(8):680-683.

[2] Severns R. History of the forward converter [J].Switching Power Magazine,IEEE,2000, 14(8):1346-1356.

[3] Ericson R W, Maksimovic D.Fundamentals of power electronics[M].2nd ed. Norwell, MA:Kluwer,2001.

[4] Rodriguez H, Ortega R,Escobar G.A new family of energy-based non-linear controllers for switched power converters[J].Proceeding IEEE ISIE, 2001(2):723-727.

[5] 曲颖,张波.电压控制型BUCK变换器DCM的精确离散模型及分叉稳定性分析[J].电子学报,2002,30(8):1253-1256.

[6] 任海鹏,刘丁.Boost变换器中混沌现象及其控制的仿真研究[J].系统仿真学报,2004,16(11):2529-2532.

[7] Chakrabarty K,Podder G,Banerjee S. Bifurcation behavior in boost converter[J]. IEEE Transactions on Power Electronics,1996,11(3):439-447.

[8] 周宇飞,陈军宇,谢智刚,等.参数共振微扰法在Boost变换器混沌控制中的实现及其优化[J].物理学报,2004,53(11):2676-2683.

[9] 卢伟国,周雒维,罗全明,等.BOOST变换器延迟反馈混沌控制及其优化[J].物理学报,2007,56(11):6275-6281.

[10] 姜丹丹,周宇飞,王诗兵,等.基于时延反馈的Boost变换器混沌化控制[J].电测与仪表,2009,46(5):16-19.

[11] 王利清,魏学业,温伟刚,等.混沌态电流模式Buck-Boost开关变换器的OGY控制[J].信息与控制,2005,34(6):742-745.

[12] 包伯成,徐建平,刘中.开关DC-DC变换器斜坡补偿的稳定性控制研究[J].电子科技大学学报,2008,37(3):397-400.

[13] Basak B,Parui S. Exploration of bifurcation and chaos in buck converter supplied from a rectifier[J].IEEE Transactions on Power Electronics,2010,25(6):1556-1564.

[14] Sira Ramirez H.A geometric approach to pulse-width modulated control in nonlinear dynamical systems[J].IEEE Transactions Automation Contral,1989，34(3)：184-187.

[15] 王新生,王琪,徐殿国. DC-DC变换器中的分岔现象综述[J].哈尔滨工业大学学报,2008,40(5):754-758.

[16] Chan W C Y，Tse C K.Study of bifurcation in current-programmed DC/DC Boost converters: from quasi-periodicity to period-doubling[J].IEEE Transactions on Circuit and System,1997,44(12):1129-1142.

Study on Nonlinear and Control Technology of A New Type of Converter

LI Shaolong，ZHOU Min，CUI Yue，WU Siyuan，LU Haosun，CHEN Jianlin

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

For some portable devices currently, the output voltage harmonics of its boost converter are not ideal, this paper puts forward a new type of 1+Dnon-isolated converter and analyses its non-linear working condition, the chaos control techniques based on continuous time delay feedback method is adopted to avoid the chaotic behavior. with a simulation results come from the simulation model setted up by Simplorer, it is verified that this converter conducted in a closed-loop system can restrain the chaotic phenomena effectively by using the delay feedback control strategy, at the same time, improve the load transient response.

1+Dnon-isolated converter; the chaos control techniques; Simplorer simulation

2016- 03- 20

李少龙(1972-)，男，硕士，讲师。研究方向：电力电子非线性及控制。周敏(1992-)，男，硕士研究生。研究方向：电力电子非线性及控制。

10.16180/j.cnki.issn1007-7820.2017.01.044

TM 46

A

1007-7820(2017)01-050-04