关于曲线积分计算方法的研究

王晓晨

辽宁铁道职业技术学院，辽宁 锦州 121000



关于曲线积分计算方法的研究

王晓晨

辽宁铁道职业技术学院，辽宁 锦州 121000

积分学的基本问题就是求一个未知函数，使其导函数恰好是某一已知函数，与微分学所研究的问题是逆向的。积分学的提出和高速发展正是建立于许多现实问题的基础之上的，它为学习和掌握更加高深的数学知识提供了一个广阔的发挥空间，是培养人的数学理性思维能力的一个好的平台，有助于良好的数学建模意识的养成，可以让学习者以一个更高的数学视角更深刻的了解微积分。通过对微积分的灵活运用，搭建了学科与学科之间互为发展的桥梁，使数学不再仅仅是其他学科用于计算的工具，而是人们必须掌握的基本能力。

曲线积分；计算方法

一、曲线积分与定积分

定积分是计算各种积分的基础，曲线积分最终都转化成定积分的计算。

曲线积分有两类：一类是对弧长的曲线积分(第一型)；另一类是对坐标的曲线积分(第二型)。这两类曲线积分的定义是完全不同的，但由于它们都是沿曲线的积分，两者之间又有密切的联系。根据平面上两类曲线积分之间的转换关系式[2]，我们可以将第一型曲线积分转换成第二型曲线积分，也可以将第二型曲线积分转换成第一型曲线积分。

二、第一型曲线积分的计算

(1.1)

例1.1设L是y2=4x从O(0,0)到A(1,2)一段，试计算第一型曲线积分ʃLyds。

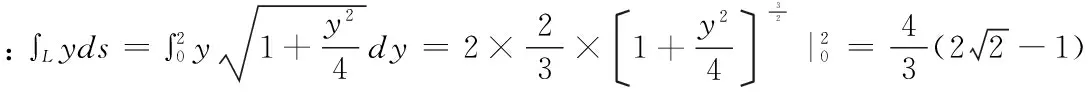
三、第二型曲线积分的计算

ʃLP(x,y)dx+Q(x,y)dy=ʃαβ[P(φ(t),φ(t))φ′(t)+Q(φ(t),φ(t))φ′(t)]dt

(1.2)

例1.2求ʃCy2dx+x2dy。其中C是上半椭圆x=acost，y=bsint，取顺时针方向。

解：根据题意计算如下：

四、第一型曲线积分与第二型曲线积分的联系

两类曲线积分通过公式[3]

(1.3)

例题1.3 把对坐标的曲线积分ʃLP(x,y)dx+Q(x,y)dy化成对弧长的曲线积分，其中L为沿上半圆周x2+y2=2x从点(0,0)到点(1,1)。

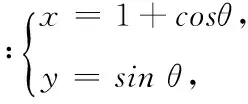
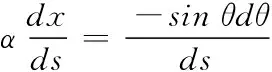
高等数学作为大学生素质教育阶段的一门必修课程，对培养人的逻辑思维能力有着至关重要的作用，微积分是一种高级的数学语言，是加深数学理论知识理解的重要基石。本文关于曲线积分的计算问题以及容易混淆的公式进行了相应的研究，并且提供了典型例题进行演示，有助于相关学者对曲线积分问题的研究。

[1]华东师范大学数学系.数学分析[M].北京:高等教育出版社,2001.

[2]赵莉.多元积分的计算与相互关系[J].张家口职业技术学院学报,2001(2).

[3]刘晓妍.“两类曲线积分之间的联系”中“夹角”与“转角”的差异[J].高等数学研究,2003(1).

O

A

1006-0049-(2017)07-0198-01