开口薄壁截面简支桥梁约束扭转的正应力分析

王艳华

（赛思达（上海）技术咨询有限公司，上海市 200070）

开口薄壁截面简支桥梁约束扭转的正应力分析

王艳华

（赛思达（上海）技术咨询有限公司，上海市 200070）

孟买地铁一号线高架简支桥梁采用了不对称开口薄壁截面梁的设计，这是一种近些年开始在城市轨道交通领域流行的新型结构，具有轻巧美观等特点。由于开口截面梁的扭转刚度相对较小且截面不对称，约束扭转效应显著，尤其是在曲线段。在对结构进行设计分析时，不能忽略扭转引起的应力效应。以孟买地铁一号线的简支曲线桥梁为例，介绍应用于该项目的约束扭转应力效应的分析方法。

不对称开口薄壁截面；约束扭转；简支桥梁

0 引言

孟买地铁一号线高架简支桥梁采用了开口薄壁截面梁的设计，这是一种近些年开始在城市轨道交通领域流行的新型结构。在上海的轨道交通项目中，8号线二期、16号线、11号线迪士尼段、17号线、8号线三期的高架桥梁都相继使用了这种类型的结构。和在轨道交通工程高架桥梁中大量使用的传统闭口箱梁相比，开口薄壁构件轻巧美观、截面形式和轨道交通设备系统完美匹配，是一种通过精细的设计分析得到的优化结构。开口截面构件扭转刚度和箱梁相比较小，加上截面的不对称性，约束扭转作用下的应力效应显著，尤其是在曲线段。要达到优化结构设计的目的，就不能忽略约束扭转引起应力效应。本文介绍了该项目设计时使用的适用于开口薄壁简支桥梁约束扭转应力效应分析方法。

1 项目概况

孟买地铁一号线(MassRapidTransitSystem)是印度首都孟买的第一条地铁线，连接Versova、Andheri、Ghatkopar三个地区，因此它被命名为VAG通道，总长度为11.4km，共设12座车站。全线为高架桥梁结构，工程总造价为432亿印度卢比，约合42.4亿人民币。

2 结构概况

本文以孟买地铁一号线高架区间使用的开口薄壁简支曲线桥梁结构为例，线路断面由两片开口薄壁梁组成，见图1。上下行线的轨道分别安装于左右两片梁的底板之上。图2为开口薄壁梁的截面尺寸图，梁截面高度为1837mm，底板宽度为4712mm，腹板厚度为240mm，底板厚度在246mm至260mm之间变化，总的截面面积为2.14m2。桥跨平面见图3，薄壁曲线梁所在线路的曲线半径R=280m。薄壁曲线梁采用了整跨预制、预应力钢绞线先张拉的施工工艺。该条线路所使用的开口薄壁简支梁的标准跨度为25m，最大跨度为30m。每片梁有4个支座，所选取的支座类型为板式橡胶支座。

图1 线路断面

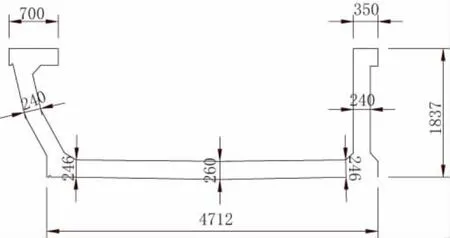
图2 截面尺寸（单位：mm）

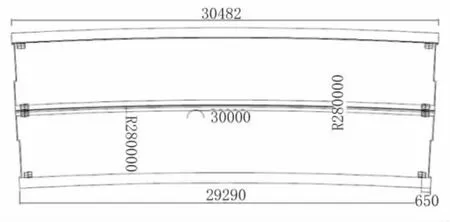
图3 桥梁平面图（单位：mm）

3 约束扭转的应力效应分析

3.1 获取截面相关参数

在进行约束扭转引起的正应力计算时，首先使用结构计算软件对截面进行分析，得到截面面积、圣-维南扭转惯性矩K、主惯性矩、主方向和水平方向的夹角、重心、扭转中心以及扇形惯性矩Iω这些相关参数。

3.2 计算扭转中心的主扇形面积

定义主扇形面积为ωC，薄壁构件截面近似用薄壁厚度中点的纤维来表示，主扇形面积是以扭转中心C为极点沿薄壁厚度中点连线建立的扇形面积。在原点处,主扇形面积为零。图4给出了该曲线简支桥梁开口薄壁截面主扇形面积的计算结果。

图4 主扇形面积（单位：m2）

3.3 截面的横向截面翘曲

在扭转的作用下，所有的薄壁梁都会产生翘曲，这意味着截面不再是一个平面。如图5所示，属于坐标x的截面上的横向曲线坐标上的任意一点在纵向发生移动。

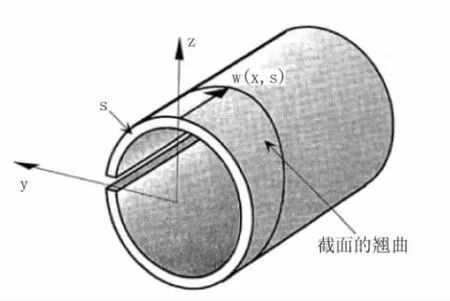
图5 扭转作用下截面的翘曲

3.4 约束扭转的微分方程

常数项由以下的边界条件确定：

不能自由旋转时：θ=0;

可以自由翘曲时：θ''=0;

不能自由翘曲时：θ'=0。

4 不同形式约束扭转的微分方程的解

在本项目中，引起约束扭转的扭矩有三种形式：集中力作用下的集中扭矩、均布荷载如自重和SIDL作用下的均布扭矩（荷载中心和扭转中心的不重合引起）和非均布扭矩（曲线效应引起）。以下对这三种情况分别进行分析：

4.1 集中扭矩

假设集中扭矩值为T,L为梁跨长度，a为集中扭矩作用点左边段的长度，b为右边段的长度。T1为左边段扭矩的定值，T2为右边段的定值。初始微分方程为：

当x∈（0，a）时，

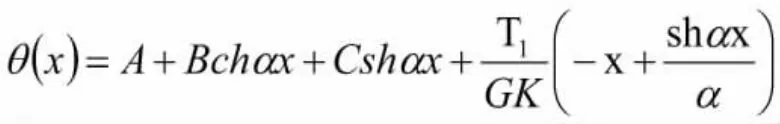
当x∈（a，L）时，

根据梁端的边界条件，得出：

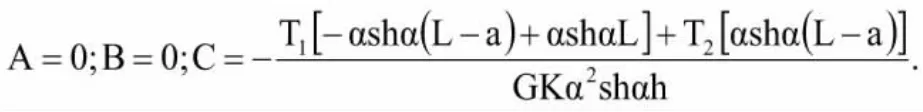
4.2 均布扭矩

设均布荷载为q,其到扭转中心的偏心距离为e，则：T（t）=T0-qet

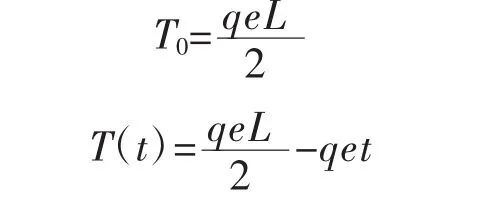
根据梁端的边界条件，得出：

4.3 曲线效应引起的非均布扭矩

在曲线段，竖向荷载如自重荷载和SIDL荷载到支座连线的距离是变化的的。假设曲线坐标 x始于结构跨端，d（x）为支座连线和x轴上的截面扭转中心的偏心距。扭矩可以根据图6表示成：

其中q为竖向荷载的强度(向上为+)，L为曲线跨的长度，R为曲线半径。

梁两端的扭矩为

图6 曲线坐标

可以得到：

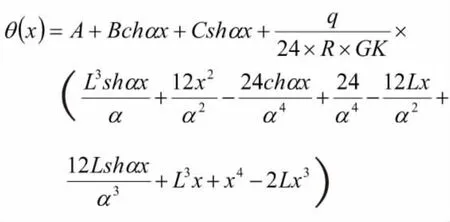
根据梁端的边界条件，得出：

5 结 语

本文给出了适用于地铁高架的开口薄壁简支梁在约束扭转下的微分方程以及约束扭转引起的正应力的计算分析方法。第4节给出的约束扭转下的正应力公式可以直接用于不同截面的开口薄壁简支梁。精细化的设计分析能够获得更优的结构，开口薄壁简支梁在城市轨道交通领域越来越广泛的应用充分说明了这一点。

[1]Jean-ArmandCalgaro.Poutresàparoisminces（薄壁截面梁）[M].巴黎：HERMES出版社,1998.

U448.21+7

：A

：1009-7716（2017）02-0066-03

10.16799/j.cnki.csdqyfh.2017.02.020

2016-11-10

王艳华（1983-），女，江苏张家港人，工程师，从事桥梁结构设计工作。