Integrated optimal method for cell formation and layout problems based on hybrid SA algorithm with fuzzy simulation①
2017-03-28ZhouBinghai周炳海LuYubin
Zhou Binghai (周炳海)Lu Yubin
(School of Mechanical Engineering, Tongji University, Shanghai 201804, P.R.China)
Integrated optimal method for cell formation and layout problems based on hybrid SA algorithm with fuzzy simulation①
Zhou Binghai (周炳海)②Lu Yubin
(School of Mechanical Engineering, Tongji University, Shanghai 201804, P.R.China)
To adapt to the complex and changeable market environment, the cell formation problems (CFPs) and the cell layout problems (CLPs) with fuzzy demands were optimized simultaneously. Firstly, CFPs and CLPs were described formally. To deal with the uncertainty fuzzy parameters brought, a chance constraint was introduced. A mathematical model was established with an objective function of minimizing intra-cell and inter-cell material handling cost. As the chance constraint of this problem could not be converted into its crisp equivalent, a hybrid simulated annealing(HSA) based on fuzzy simulation was put forward. Finally, simulation experiments were conducted under different confidence levels. Results indicated that the proposed hybrid algorithm was feasible and effective.
fuzzy demand, cell formation and cell layout problem, chance constraint, fuzzy simulation, simulated annealing algorithm
0 Introduction
As one of the first applications of group technology (GT) to factory reconfiguration and shop floor layout design, cellular manufacturing systems (CMSs) can reduce material handling cost, set-up time, manufacturing lead time, tooling cost, work in process, lot sizes, throughput times, labor cost and production equipment cost. Also CMSs can enhance manufacturing capability, workers’ satisfactions and flexibility along with a lot of other advantages[1].
Cell formation (CF) and cell layout (CL) (including intra-cell machine layout and inter-cell layout) are two basic and important steps in the design of CMSs. Over the past decades, many researchers have predominantly focused on solving CFPs, as it is the first stage in CMSs. Many analytical methods have been developed as a result of this massive movement. Ref.[2] proposed a methodology to incorporate new parts and machines into an existing cellular manufacturing system. Ref.[3] introduced a newly developed bacteria foraging algorithm based on operation sequences to solve CFPs. Ref.[4] solved the CFPs and minimized the number of voids and exceptional elements in a three dimensional machine-part-worker incidence matrix. Ref.[5] established a p-median model to find the optimal number of machine cells and associated part families considering real-world operation sequences and production volumes for parts.
Some researchers have also surveyed both CFPs and CLPs. Ref.[6] developed a class algorithm that identified not only cells but also sequence of machines in the cells in a simultaneous fashion using sequence data. But they did not regard inter-cell movements. Ref.[7] and Ref.[8] proposed a two-phase approach to tackle the CFPs and CLPs with consideration of intra-cell and inter-cell part movements. In the first phase, a mathematical model with multi-objective function was formed to obtain the machine cells and part families.Afterwards, in the second phase, another mathematical model with single-objective function was presented. The output of its first phase was employed to the second mathematical model. Actually, this research covered the CFPs and CLPs, but not in an integrated mathematical model.
In recent years, some researchers investigated the CFPs or the CLPs in dynamic environment in adaptation to real-world manufacturing systems. Ref.[9] established a multi-objective mixed-integer nonlinear programming model and used GAMS software to solve CFPs and CLPs in dynamic environment with predefined demands in different periods. However, this method cannot solve CFPs with uncertain demands. Ref.[10] presented a dynamic multi-objective mixed mathematical model for CLPs with probabilistic demand and machine reliability analysis. Refs[11,12] established three types of fuzzy programming models to solve the capacitated CLPs with fuzzy demands. The three models are the expected cost minimization model, fuzzy minimization model and credibility maximization model respectively. Ref.[13] adopted a hybrid GA with fuzzy simulation to solve CLPs in uncertain environment. Although this hybrid algorithm could handle uncertainty fuzzy demands brought, as GA has to set a number of uncertain parameters and it has a slow convergence speed, and fuzzy simulation need lots of time when computing due to its statistics essence, this hybrid algorithm would lead to much more searching time and alternative solutions.
Among the literatures mentioned above, most studies, however, have only addressed CFPs and CLPs sequentially or independently, and despite that these two decisions are interrelated and impact each other.In this paper, integrated CFPs and CLPs are considered simultaneously with the assumption that demands of parts are fuzzy numbers with different member functions. To solve such a problem, an integrated model is established based on chance constraints for the objective function and a hybrid simulated annealing (HSA) with fuzzy simulation is proposed.
1 Problem definition and formulation
1.1 Problem definition
Considering a cellular manufacturing system which produces P kinds of products wih M different machines, the demand volume for parts is assumed as fuzzy numbers with different member functions. Each part type may have a number of processing routes. Machines are located in linear arrangement within cells, while cells themselves are located in some predetermined compulsory places in a plant.The problem is to select a processing route for each product, determine the location of each machine, and arrange cells into the plant in a way that total material handling cost is minimized.
The problem is also formulated under the following assumptions: (1) the member functions followed by product demands are known; (2) all machines have same dimensions and are placed in the locations with same dimensions.The distance between any two adjacent locations is the same and the maximum and minimum of the cell size are known in advance; (3) processing routes of parts are known and parts must be processed based on operation sequence readily available from the route sheet of parts; (4) penalties for forward and backtracking movements in cells are different, and that for inter-cell movements is the highest; (5) consecutive operations of one part type are not allowed to be processed on the same machine.
According to assumption (2), following Eq.(1) and constraint (2) can be inferred.
Dmi, mj=D×|mi-mj|
(1)
(2)
where miand mjare machine numbers, mi, mj={1,2,…,M}, Dmi,mjdenotes the distance between any two machines in Eq.(1). D is the distance between two adjacent locations in cells. In constraint (2), Wlmkipis a binary variable, which will be 1 if operation i of part p is performed on machine m which is located in location l of cell k, otherwise it will be 0. MUand MLare lower and upper bounds of locations in a cell.
According to above assumption (4), Eq.(3)~(5) can be derived.
(3)
(4)
(5)
In Eqs(3)~(5), CF, CBand CEXrespectively represent total forward, backtracking and inter-cell material handling cost while Cf, Cband Cexrepresent forward, backtracking and inter-cell unit cost of material handling respectively. Apikand Bpikare decision variables, Apikequals to lki+1p-lkipif machine miperforming operation i of part p is in front of machine mi+1performing operation i+1 of part p, otherwise Apikis 0. Bpikequals to lki+1p-lkipif machine miperforming operation i of part p is behind machine mi+1performing operation i+1 of part p, otherwise Bpikis 0. lkipis the location number of machine miperforming operation i of part p. k and k’ are cell numbers, k,k′={1,2,…,K}
Eqs(6) and (7) are constraints for Apikand Bpik
Apik-Bpik=lki+1p-lkip
(6)
Apik×Bpik=0
(7)
Therefore, the objective function of minimizing intra-cell and inter-cell material handing cost is as Eq.(8).
(8)
1.2 Chance constraints for objective function
To handle the uncertainty fuzzy parameters brought, chance constraints for objective function are adopted as Ref.[11] did. Chance constrained programming is applied to solve the practical optimization problems with the requirement that the chance constraints should hold with at least some given confidence levels provided as an appropriate safety margin by the decision-maker.
Constraint (9) ensures the credibility of the optimal solution C0must not be less than confidence level α. Constraint (10) shows how to calculate Cr
Cr={x∈X|C(ξ1,ξ2,…,ξp)≤C0}>=a
(9)
(10)
where Cr is the credibility measure, α is the predetermined confidence level, ξpis the demand fuzzy number of product p. Pos and Nec denote the possibility and necessity of a fuzzy event, r is a reference value.
2 Proposed algorithm
Certain models of integrated CFP and CLP have been proved to be NP-hard problems in Ref.[14]. It should be noted that considering fuzzy data amounts for demand does increase complexity of the problem, and may consequently make the exact optimization methods become very difficult and sometimes impossible. Therefore, in the next section, a novel simulated annealing algorithm with fuzzy simulation is proposed to solve the developed model.
2.1 Hierarchical scheme for coding
In this paper, a three-layer hierarchical scheme for encoding is proposed.Table 1 shows a general example of the chromosome for a problem with p parts and M machines.

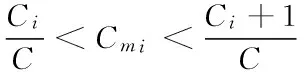
The last layer, which also consists of M genes, is related to the locations which the machines are assigned to. Allele lmmof each gene is a real number randomly generated from 0 to 1. Supposing machines mi1, mi2,…, mijare divided into the same cell according to the rule of the second layer. lmi1,lmi2,…,lmijwill be sorted which are codes for corresponding machines mi1,mi2,…,mijfrom small to large. Based on the sort, machines are assigned to the locations.
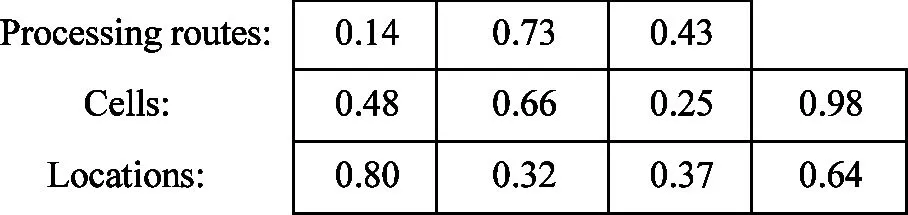
The encoding rule is explained with a numerical example. Suppose that a cellular manufacturing system consists of 3 kinds of parts and 4 machines. The three kind types of parts have 3, 4 and 3 processing routes respectively. According to the code shown in Table 2, the solution of CFP and CLP is as follows: the 3 parts select its first, third and second processing routes respectively. Machine 1 and machine 3 belong to location 2 and location 1 of cell 1. Machine 2 and 4 belong to location 1 and 2 of cell 2.
Table 1 General encoding rule
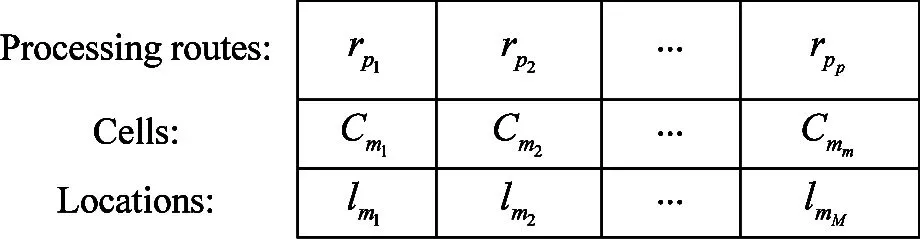
Table 2 A numerical example of encoding
2.2 Simulated annealing algorithm based on fuzzy simulation
One way of solving chance constrained programming with fuzzy parameters is to convert the chance constraints to their respective crisp equivalents. This process is usually a hard work and only successful for some special cases. As the mathematical model of this paper cannot meet the requirements in Ref.[11] reviewed, a fuzzy simulation is proposed in this paper to solve the above chance constraints referring to Ref.[15].
Fuzzy simulation technique is an applicable form of the Monte-Carlo simulation. Considering constraint (8), whenever we need to calculate the fitness values of chromosomes in different iterations of the simulated annealing algorithm, the fuzzy simulation approach will be employed. In the following parts, the steps of SA based on fuzzy simulation technique in estimating the optimal solution for integrated CFP and CLP are introduced.
Step 1: Produce random variables Yp1, Yp2,…,YpN, p={1,2,…,P} on the condition that Vpk=μp(Ypk)≥ε. Ypkis the kth selected random variable from fuzzy number ξp(demand volume of p), ε is a very small positive real number and μpis the membership function of fuzzy number ξp, N is the number of the simulation process iterations.
Step 2: For each j there would be a complete set of certain numbers, which are presented as Yk, showing the amount of demand.
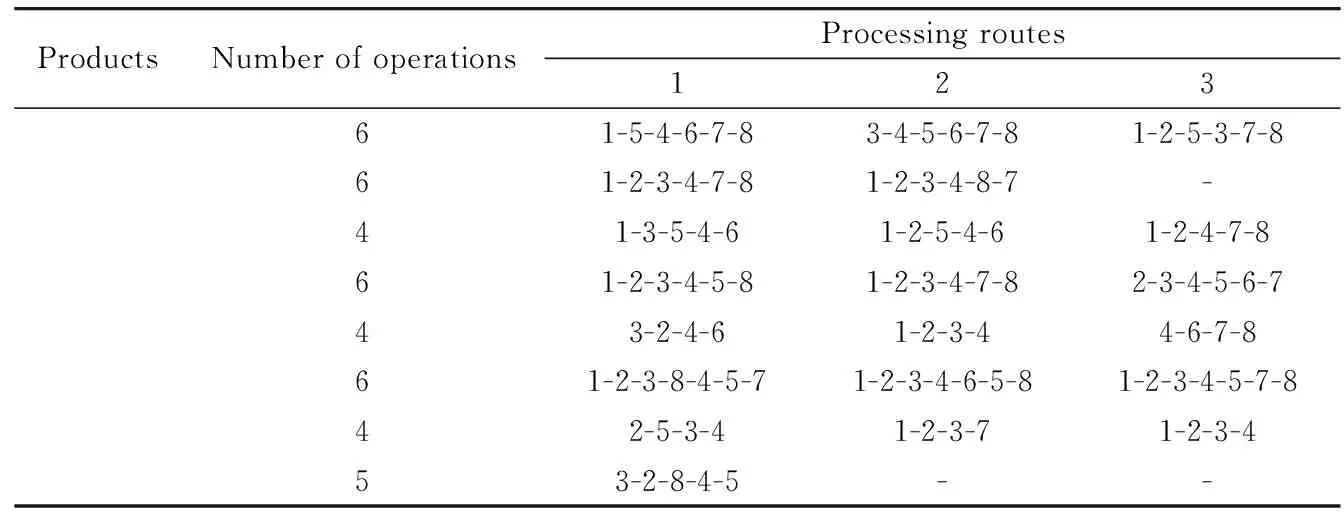
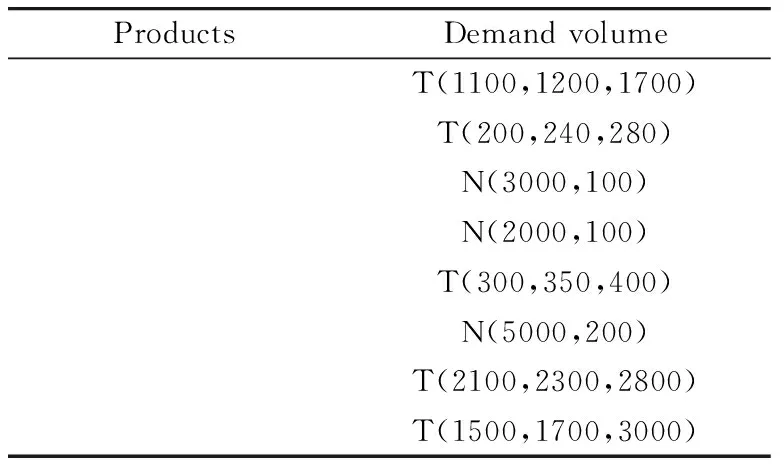
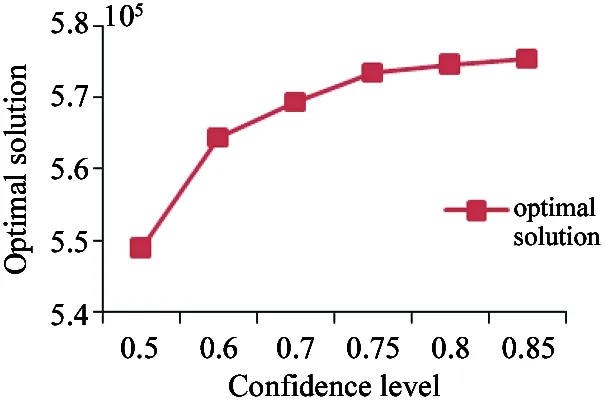
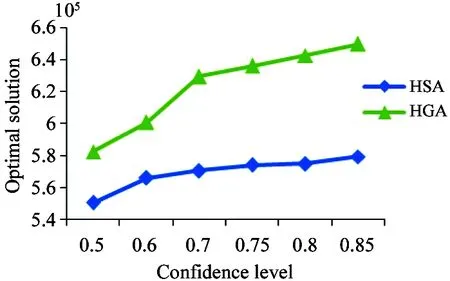
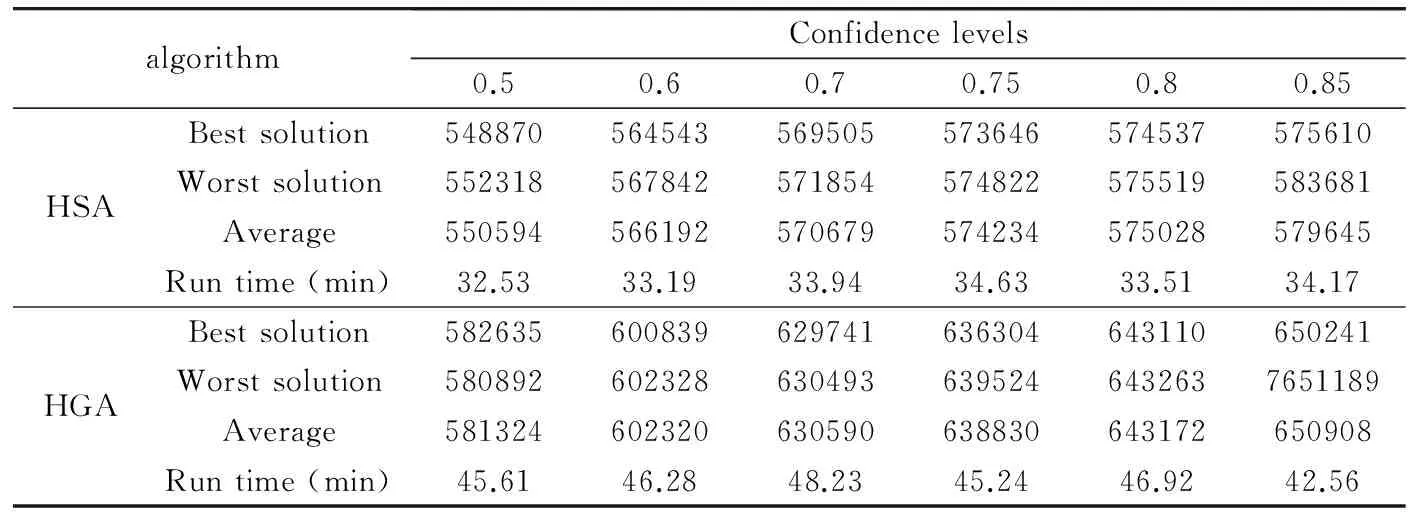
Yk={Ypk|1 Step 3: Use SA to calculate the total cost by substituting Ykwith ξp. Ck=C(x,Yk) (11) Step 4: Calculate the possibility of Vkaccording to Eq.(12) Vk=min(V1k, V2k,…,VPk) (12) Step 5: Calculate the amount of Pos(C(x,Yi) Pos(C(x, Yi) (13) Step 6: Calculate the credibility Crkof total cost of kth fuzzy simulation according to Eq.(14) converted from Eq.(10). k={1,2,…,K} (14) Step 7: Repeat the 5th and 6th steps for N times to calculate the respective credibility of total cost when simulation is conducted for one time,then go to step 8. Step 8: Calculate the optimal solution that meets chance constraints (8) and (9) by C0=min{Ck|Crk≥α} (15) To validate the model and evaluate the performance of proposed hybrid SA, two experiments are conducted: (1) a medium-scale numerical example is solved by proposed HSA under different confidence levels. Besides, the influence of different confidence levels on the experimental results is analyzed; (2) HGA proposed by Ref.[12] are also used to solve the above numerical example. The obtained results are compared with those generated by proposed HSA. 3.1 Sensitivity analysis of the confidence levels Considering a cellular manufacturing system with 8 different kinds of products, the number of machines is 8 which should be located in discrete candidate locations of 2 cells. Table 3 shows the available processing routes to process the products. The amount of demand is uncertain and stated in fuzzy numbers. It is considered triangular fuzzy numbers for P1, P2, P5, P7, P8and normal for p3, p4, p6. Complementary data of demand is provided in Table 4.Suppose Cf, Cband Cexare 3, 5 and 7 respectively. D is 1 and Dk, k′is 2. The proposed algorithm is coded in MATLAB R2012a and solved in PC with 2.67GHz Intel Core processor and 2GB of RAM. The SA parameters are set as follows: initial temperature Tin=15,000, final temperature Tf=100, rate of cooling α=0.98, length of Markov L=24, stopping criteria also as 30 iterations without any improvement. Iteration N of fuzzy simulation is 1000. The numerical example above is solved under different confidence levels. The best chromosome obtained is shown in Table 5. The convergence curves of proposed HSA under α=0.75 and α=0.70 are shown in Fig.1. Table 3 Processing routes of parts Table 4 Member functions followed by parts demands From the best chromosome shown in Table 5, result of CFP and CLP are obtained: the first 6 machines are assigned into the 6th, 5th, 4th, 3rd, 2nd, and 1st location of cell 1 respectively. Machine 5 and machine 6 are assigned into location 2 and location 1 of cell 2. The 8 products select their 2nd, 1st, 1st, 3rd, 2nd, 3rd, 3rd and 1st processing routes respectively. The optimal cost obtained by coding in MATLAB is 573646. Effects of different confidence levels on optimal solution are depicted in Fig.2. As seen from Fig.2, the solution quality decreases with the increase of confidence level.The results can be explained with the fact that, when confidence level increases, solutions should have a higher ability of handling uncertainty. According to Eq.(9), for any solution, the corresponding overall fitness value computed by fuzzy simulation increases, leading to higher cost of the optimal solution acquired by proposed HSA. Table 5 Corresponding chromosome of optimum solution Fig.1 Convergence of optimal solution Fig.2 Sensitive analysis of confidence level 3.2 Comparison with HGA In this section, hybrid genetic algorithm(HGA) proposed in Ref.[12] and HSA proposed in this paper are used to solve the above numerical example. The parameters of HGA are considered as: population size 40, crossover rate 0.8, mutation rate 0.2, stopping criteria as 30 iterations without any improvement, or producing 100 generations. In order to reduce deviation fuzzy parameters brought, the problem is solved for 10 times by both of the two algorithms. Detailed computing results can be seen in Table 6. Comparative results are depicted vividly in Fig.3 and Fig.4. Fig.3 The best solution of HSA and HGA algorithm in different confidence levels Fig.4 Computing time of HSA and HSA As seen in Fig.3 and Fig.4, no matter from the view of material handling cost or computing time, the solution obtained by proposed HSA in this paper is better than that obtained by HGA. These results can be explained with computing process of HGA. In the fuzzy simulation part of HGA, the fitness value of one solution is calculated with demands randomly generated for many times according to statistical principle. It may be exactly the calculation method that has a negative influence for retaining excellent genes of GA.This is why the cost of the optimal solution obtained by HGA is higher than that obtained by HSA. From Fig.4, as the convergence speed of GA is slower than SA, and when calculating fitness value of one solution, every time fuzzy simulation is used, GA should be used first as depicted in algorithm steps of Section 2.2. That is the reason that HSA would consume more time. Table 6 The best solution of last instance within different confidence level In order to solve CFPs and CLPs with fuzzy demands, HSA is proposed based on fuzzy simulation after chance constraints for the objective function is introduced to handle the uncertainty fuzzy parameters brought. The results of numerical examples demonstrates that the HSA could find good solutions in a reasonable time, showing its good adaptation. Compared with other algorithms for solving chance constraint programming, the proposed HSA could find better solutions in shorter time. Therefore, the proposed HSA based on fuzzy simulation is feasible and effective. In the future, CFPs and CLPs with resource assignment problems in the fuzzy environment could be further discussed. [1] Hearago S S. Group technology and cellular manufacturing. IEEE Transaction on Systems, Man and Cybernetic, 1994, 24(2): 203-215 [2] Bhandwale A, Kesavadas T. A methodology to incorporate product mix variations in cellular manufacturing. Journal of Intelligent Manufacturing, 2008, 19(1): 71-85 [3] Nouri H, Tang S H, Hang T B T, et al. BASE: a bacteria foraging algorithm for cell formation with sequence data. Journal of Manufacturing Systems, 2010, 29(2): 102-110 [4] Mahdavi I, Aalaei A, Paydar M M, et al. A new mathematical model for integrating all incidence matrices in multi-dimensional cellular manufacturing system. Journal of Manufacturing Systems, 2012, 31(2): 214-223 [5] Won Y, Currie K. An effective P-median model considering production factors in machine cell/part family formation. Journal of Manufacturing Systems, 2006, 25(1): 58-64 [6] Mahdavi I, Mahadevan B. CLASS: an algorithm for cellular manufacturing system and layout design using sequence data. Robotics and Computer Integrated Manufacturing, 2008, 24(3): 488-497 [7] Chan F T S, Lau K W, Chan P L Y, et al. Two-stage approach for machine-part grouping and cell layout problems. Robotics and Computer Integrated Manufacturing, 2006, 22(3): 217-238 [8] Chan F T S, Lau K W, Chan L Y, et al. Cell formation problem with consideration of both intracellular and intercellular movements. International Journal of Production Research, 2008, 46(10): 2589-2620 [9] Kia R, Shirazi H, Javadian N, et al. A multi-objective model for designing a group layout of a dynamic cellular manufacturing system. Journal of Industrial Engineering International, 2013, 9(1): 1-14 [10] Aghajani A, Didehbani S A, Zadahmad M, et al. A multi-objective mathematical model for cellular manufacturing systems design with probabilistic demand and machine reliability analysis. International Journal of Advance Manufacturing technology, 2014,75(5~8):755-770 [11] Liu B D, Iwamura K. Chance constrained programming with fuzzyparameters. Fuzzy Sets and Systems, 1998, 94(2): 227-237 [12] Zhou J, Liu B D. Modeling capacitated location-allocation problemwith fuzzy demands. Computers and Industrial Engineering, 2007, 53(3):454- 468 [13] Nasab H H. A hybrid fuzzy-GA algorithm for the integrated machine allocation problem with fuzzy demands. Applied Soft Computing, 2014, 23(5): 417-431 [14] King J, Nakornchai V. Machine-component group formation in group technology: review and extension. International Journal of Production Research, 1982, 20(2):117-133 [15] Iwaruma K, Liu B D. A genetic algorithm for chance constrained programming. Journal of Information & Optimization Sciences, 1996, 17(2): 409- 422 Zhou Binghai, born in 1965. He received his M.S. and Ph.D degrees respectively from School of Mechanical Engineering, Shanghai Jiaotong University in 1992 and 2001. He is a professor, a Ph.D supervisor in School of Mechanical Engineering, Tongji University. He is the author of more than 140 scientific papers. His current research interests are scheduling, modeling, simulation and control for manufacturing systems, integrated manufacturing technology. 10.3772/j.issn.1006-6748.2017.01.001 ①Supported by the National Natural Science Foundation of China (No. 61273035, 71471135). ②To whom correspondence should be addressed. E-mail: bhzhou@tongji.edu.cn Received on Feb. 14, 2016,3 Experiments and analysis



4 Conclusions
杂志排行
High Technology Letters的其它文章
- A GA approach to vehicle routing problem with time windows considering loading constraints①
- Research on intelligent ultrasonic thickness measurement system applied to large area of hull①
- Coupling methods of global climate models and regional climate models①
- A study on TCP performance of crowdsourced live streaming①
- Docking process on hybrid self-reconfigurable modular robots①
- A clustered routing protocol based on energy and link quality in WSNs①
