巧构直角坐标系 妙解平面向量题
2017-03-28江苏韩文美陆东标
江苏 韩文美 陆东标
(作者单位:江苏省张家港职业教育中心)
巧构直角坐标系 妙解平面向量题

平面向量是衔接数学中代数与几何的纽带,沟通“数”与“形”的桥梁,是数形结合的典范.其优势在于可以将几何问题坐标化、符号化、数量化,从而将几何推理转化为代数运算,这也决定了向量法在解题中有着广泛的应用.而在解决平面向量问题中,通过巧妙构造直角坐标系,利用直角坐标法来求解相应的平面向量问题,也是高考中比较常见的一类技巧方法.
1.巧构坐标系,妙求参数值

【分析】通过三角形形状的特殊化,并结合构造平面直角坐标系,利用平面向量的坐标运算来转化对应的线性运算,进而求解相应的参数值问题.
【解析】不妨设AC⊥AB,且AB=4,AC=3,以A为坐标原点,AB,AC所在直线分别为x轴、y轴建立直角坐标系,图略.

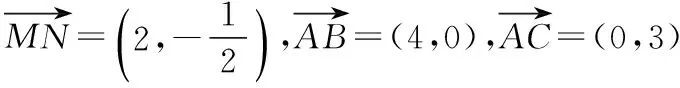

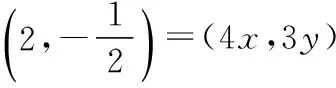

【点评】解决此类平面向量的参数值问题时,常规方法是结合平面几何图形,利用平面向量中的三角形法则,通过平面向量的线性运算进行转化,对比平面向量的线性关系式来求解相应的参数值,过程比较繁杂,计算量也大.而通过平面图形的特殊化思维,结合平面直角坐标系的巧妙构造,利用特殊化情况下坐标运算来处理一般性问题,目标性强,方法巧妙,解答简单.

【解析】不妨设AD⊥AB,且AB=4,AD=3,以A为坐标原点,AB,AC所在直线分别为x轴、y轴建立直角坐标系.


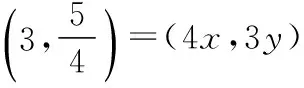
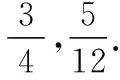
2.巧构坐标系,妙解模问题
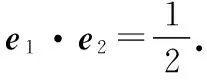
【分析】根据题目条件确定两平面单位向量的夹角,通过建立相应的平面直角坐标系,设出平面向量b的坐标,利用平面向量的数量积分别确定坐标参数,进而求解平面向量b的坐标,即可求解相应的模.
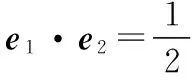
设b=(x,y),则由b·e1=b·e2=1,


【点评】解决平面向量的模问题,往往可以通过平面向量的数量积公式来求解.而利用题目条件建立相应的平面直角坐标系,利用平面向量的坐标结合模的定义来确定相应的模问题是非常巧妙的一种方法.关键是合理构造直角坐标系,结合条件建立与坐标有关的参数关系式.
【变式2】已知平面向量a,b,|a|=1,|b|=2,a·b=1,若平面向量c满足a·c=b·c=2,则|c|=________.
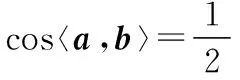
设c=(x,y),则由a·c=b·c=2,
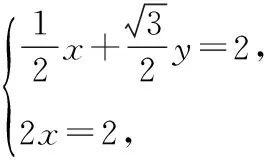

3.巧构坐标系,妙解数量积
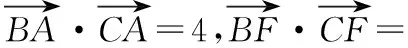

【分析】通过建立平面直角坐标系,设出点B,A的坐标,结合相关平面向量的坐标,利用平面向量的数量积来转化,通过求解所设的坐标值的整体代换即可达到求解相应向量的数量积问题.
【解析】以D为坐标原点,BC为x轴,BC的中垂线为y轴建立平面直角坐标系,设B(―a,0),A(b,c),则C(a,0),
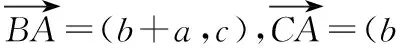
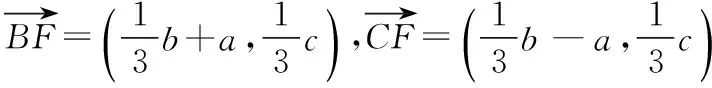
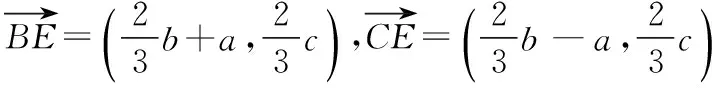

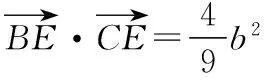
【点评】解决平面向量的数量积问题,往往通过平面线性的线性运算,结合平面向量数量积的定义与关系式来转化.在解决平面向量数量积问题中,通过巧妙构造坐标系,利用坐标法来求解相应的平面向量问题,也是高考中比较常见的一类技巧方法.
4.巧构坐标系,妙求代数式
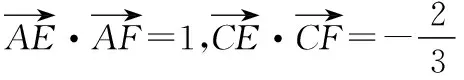
( )
【分析】结合菱形的特征建立平面直角坐标系,利用平面向量的坐标法以及数量积公式建立相应的方程组,进而通过方程组的转化来达到求解代数式的值.
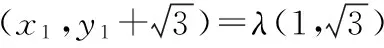


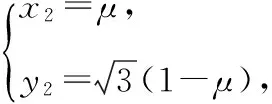
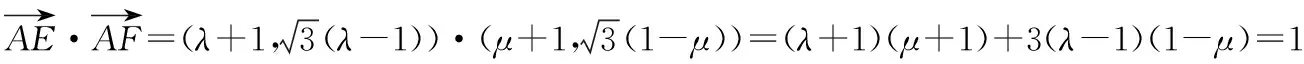
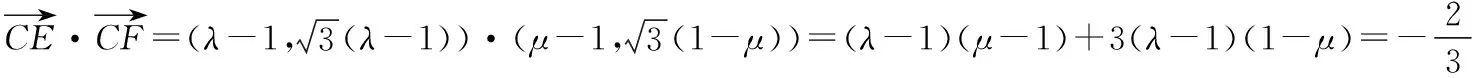
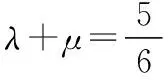
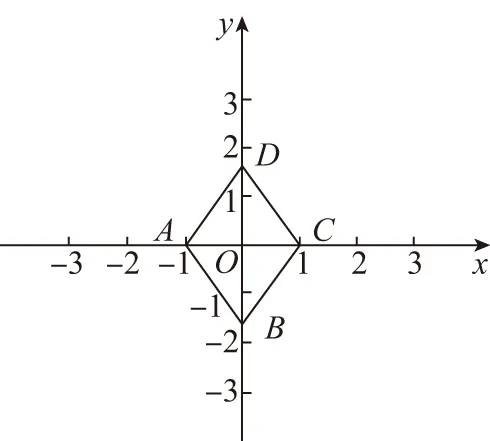
【点评】解决平面向量中的代数式问题,往往利用平面向量的线性运算及数量积等相关知识来处理.而通过建立平面直角坐标系,把几何问题转化为代数问题,通过平面向量的坐标代数式,利用平面向量的数量积来转化与应用,进而达到求解代数式的值的目的.
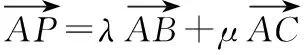
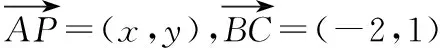
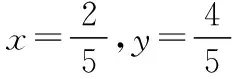
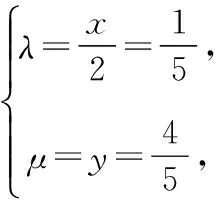
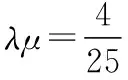
5.巧构坐标系,妙解最值题

( )
【分析】结合题目条件加以分析判断△ABC的形状特征,通过构造平面直角坐标系,把平面向量的线性关系转化为坐标关系,结合两点间的距离公式,利用三角函数的图象与性质来确定平面向量的最值问题.

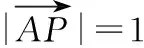


【点评】解决平面向量中的相关最值问题,通过巧妙构造坐标系,利用坐标法来求解相应的向量问题,把平面向量的线性运算、模、数量积等问题加以转化,利用平面向量的几何意义、函数的性质、三角函数或不等式等来确定对应的最值问题,有效转化,思路清晰,解法巧妙.
( )
A.13 B.15 C.19 D.21
【解析】以A点为坐标原点,AB,AC所在直线为x轴、y轴建立平面直角坐标系(图略),
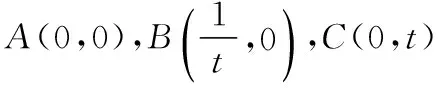
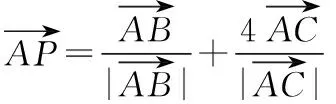



6.巧构坐标系,妙求范围题
( )
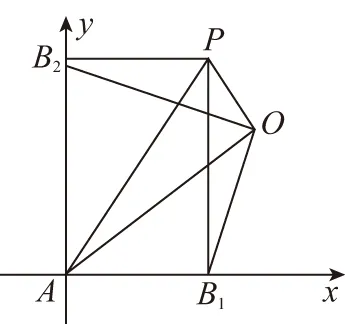
【分析】根据条件联想到通过建立平面直角坐标系来解决,主要是观察到A,B1,P,B2构成一个矩形,而向量与坐标有着密切的联系,通过已知向量的模的不等式来建立相应的不等式,结合模的定义,利用不等式的性质来转化与应用,进而达到确定相关模的取值范围的目的.
【解析】根据条件知A,B1,P,B2构成一个矩形AB1PB2,
以AB1,PB2所在直线为坐标轴建立直角坐标系,



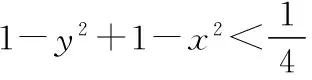
又由(x-a)2+y2=1,
得x2+y2+a2=1+2ax≤1+a2+x2,则y2≤1,
同理由x2+(y-b)2=1得x2≤1,即x2+y2≤2,②
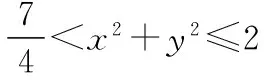
故答案为D.
【点评】解决平面向量中的相关取值范围问题,往往结合题目条件,经过求解转化,应用排除法来分析与求解.另外,建立平面直角坐标系,通过把问题坐标化,关键是应用不等式性质与平面向量中的相关几何意义来确定与之有关的取值范围.
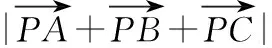
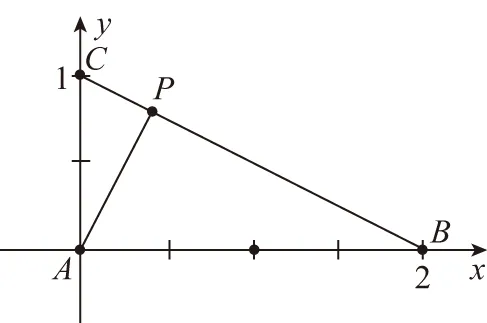
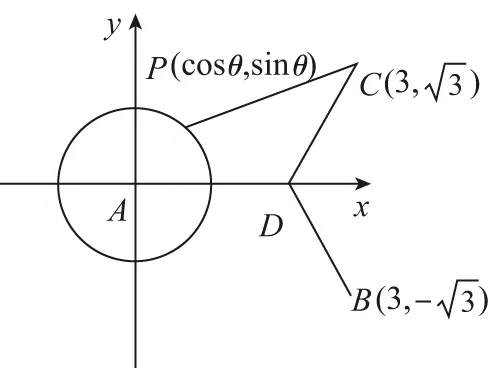
【解析】由圆周角的性质得点B是在以AC为直径的圆O上,
以AC所在直线为x轴,AC的垂直平分线为y轴建立平面直角坐标系,如图所示,
则有A(-1,0),C(1,0),P(2,0),
设B(x,y),x∈[-1,1],x2+y2=1,



7.巧构坐标系,妙解创新题

( )
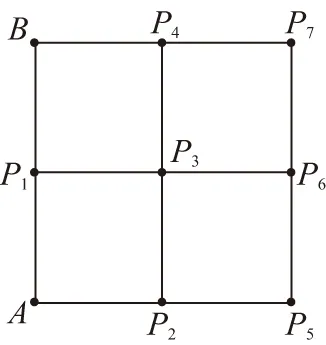
A.7 B.5 C.3 D.1
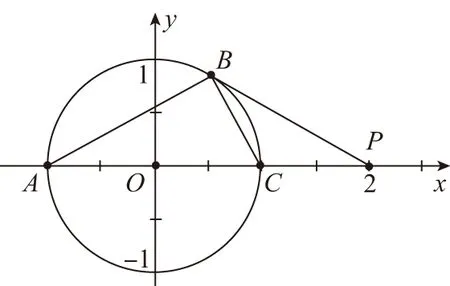
【分析】通过建立平面直角坐标系,进而确定各相应点的坐标,利用平面向量的数量积的坐标运算来分析,结合数量积的不同结合,达到应用的目的.
【解析】以A为坐标原点,AB所在直线为y轴建立平面直角坐标系,对应的点A(0,0),B(0,2),P1(0,1),P2(1,0),P3(1,1),P4(1,2),P5(2,0),P6(2,1),P7(2,2),

【点评】解决平面向量的创新应用问题,往往要结合题目条件,选择最恰当的方法来处理创新问题.而涉及与平面几何有关的平面向量问题,可采用平面直角坐标系的巧妙建立,把平面向量问题与平面几何问题加以有效转化,可以使创新问题的解决朝着方便简捷的方向转化.
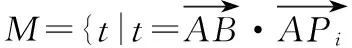
( )

A.7 B.5 C.3 D.1



(作者单位:江苏省张家港职业教育中心)
