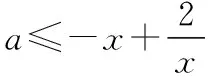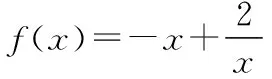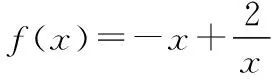山重水复疑无路 柳暗花明又一村
——例谈解题过程受阻的原因和对策
2017-03-28安徽朱启州
安徽 朱启州
(作者单位:安徽省淮北市杜集区教育局教研室)
山重水复疑无路 柳暗花明又一村
——例谈解题过程受阻的原因和对策

在数学解题中,我们常有解题解不下去的时候,有时是越解越没信心做下去,有时是思维受阻无计可施,有时是因思维定式钻进了牛角尖,种种困境不一而足.遇到这种让人心烦的情况怎么办?现从原因与对策两个方面谈一谈,供大家参考.
一、解题思路正确,因不当变形,解不下去

下面是某学生解题历程,让我们看看是什么原因造成解不下去.

要判断f′(x)的符号,关键是判断分子的符号,由此来确定原函数在区间(0,1]上的单调性,进一步求得最大值的表达式,于是可求出参数a的值.这种想法是没问题的,但这种情况下我们常需对上式中的分子因式分解,观察发现对ax2-2ax-2分解不易,转而对其中的参数a讨论,于是陷入困境.
【点拨】我们注意到a>0这个条件,对f′(x)换一种变形方式如何?
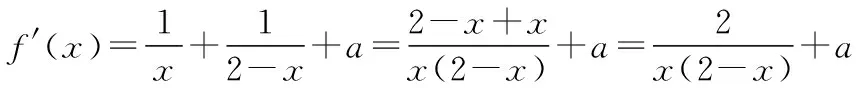
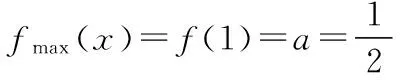
【评析】知识没问题,思路也正确,为什么会越做越没头绪了呢?由于受思维定式的影响,我们习惯地将f′(x)化为(1)的形式,而ax2-2ax-2不易继续变形,对参数a讨论又过于繁杂,而f′(x)换一种变形方式就可顺利求解.当我们因不当形变陷入困境时,不防换一种方法去思考.
二、运用常规方法,解题陷入繁杂运算,解不下去
【例2】讨论关于x的方程lg(-x2+x+2)=lg(1-k-x)解的情况.
下面是某位学生的解题历程,让我们看看是什么原因造成解不下去.
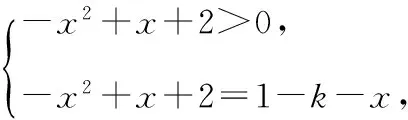
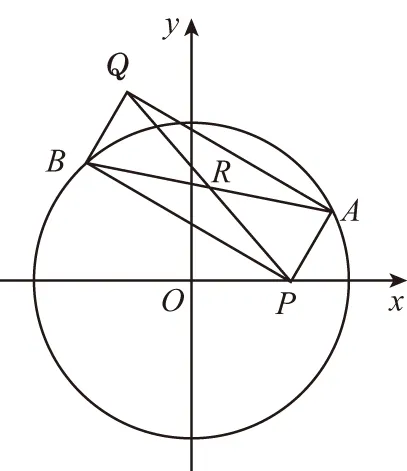
所以x2-2x-1-k=0 (-1 所以Δ=4+4(1+k)≥0,通过求根公式或用韦达定理列不等关系,讨论两根x1,x2的分布,结果解题陷入复杂的运算,解不下去. 【点拨】解至x2-2x-1-k=0 (-1 【解析】由x2-2x-1-k=0 (-1 得x2-2x=k+1, 可设y1=x2-2x,y2=k+1(-1 画图象,如图,观察图象,知当k+1≥3,或k+1<-1时,即k≥2,或k<-2时,方程无解; 当k=-2,或-1≤k<2时,有唯一解; 当-2≤k<-1时,有两解. 【评析】数形结合与分类讨论都是重要的数学思想方法,常可化腐朽为神奇. 【例3】如图,已知P(4,0)是圆x2+y2=36内一点,A,B是圆上两动点,且满足∠APB=90°,则矩形APBQ的顶点Q的轨迹方程为________. 某学生是这样解的: 设点Q的坐标为(x,y),A(x1,y1),B(x2,y2), 由矩形APBQ的两对角线交点R既是PQ中点,又是AB中点,得 x1+x2=x+4,①y1+y2=y,② 又A,B两点在圆x2+y2=36上, (x1-4)(x2-4)+y1y2=0, 即x1x2+y1y2-4(x1+x2)+16=0.⑤ 联立上述五个式子,消去x1,x2,y1,y2,找到x,y之间的关系,这一点做到真需要一点运算技巧,一般同学恐怕没有耐心做下去. 【解析】由∠APB=90°,得|AP|2+|BP|2=|PQ|2, 将①③④整体代入上式并整理,可得顶点Q的轨迹方程为x2+y2=56. 【评析】设参数过多或隐含条件挖掘不充分常造成上面这种困难局面. (1)求角C的大小; 【评析】解题中我们常根据解题经验会对问题解题思路有一个预设,关键是要随着解题的深入要随时矫正预设的解题方向和思路. 【例5】已知点O为△ABC的外接圆圆心,且|AC|=4, 【解析】作直径AD,连接CD,BD,则∠ACD=∠ABD=90°,并设∠CAD=α,∠BAD=β. 【评析】解题找不到着手点,常因问题隐含条件的挖掘不够或题设条件没充分利用.一般思考起点选择从问题条件、解题目标、解题方法等方面着手,正确的图形、特殊情形、类似问题等常能启发思考. 【例6】若关于x的不等式x2+ax-2>0在区间[1,2]上有解,则实数a的取值范围为________. 这是某校高三期末试题,有同学用分类方法求解得出了正确结果,但做得很辛苦,不少同学半途而废. 【点拨】问题实质就是“存在x0∈[1,2],使x2+ax-2>0”,其否定是“对任意x∈[1,2],都有x2+ax-2≤0”,于是问题转化为“不等式x2+ax-2≤0在区间[1,2]上恒成立,求实数a的取值范围”,解这一问题就容易多了. 所以fmin(x)=f(2)=-1, 所以不等式x2+ax-2≤0在区间[1,2]上恒成立,a≤-1, 即不等式x2+ax-2>0在区间[1,2]上有解实数a的范围是(-1,+). 【评析】“穷则思变”,解题中要注意思维的变通性,要善于观察、联想、转化,根据问题不同情况灵活制定解题方案. (作者单位:安徽省淮北市杜集区教育局教研室)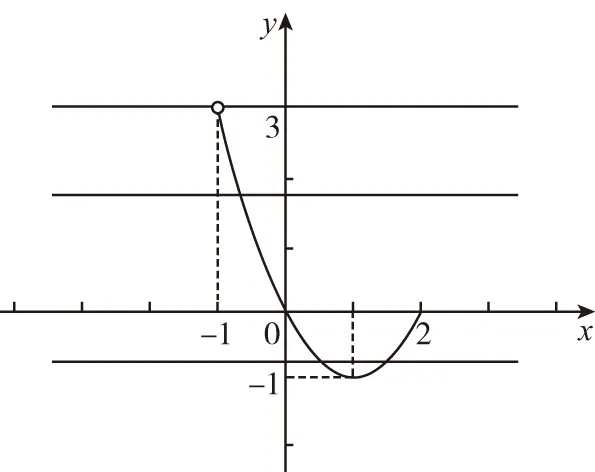
三、选用关系不当,化简困难,解不下去

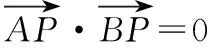
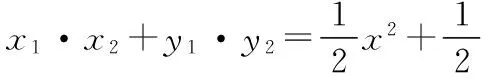

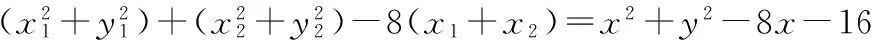
四、因解题预设,思维受阻,解不下去
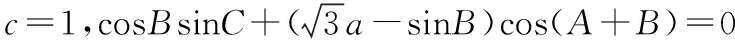
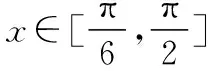
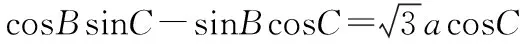
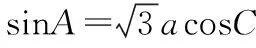

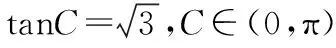
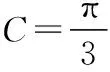
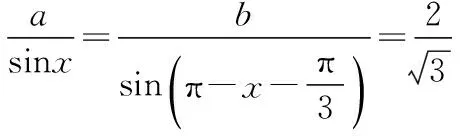
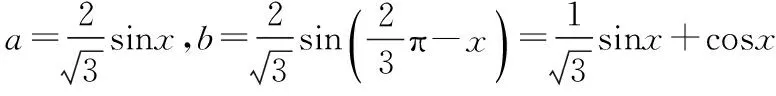
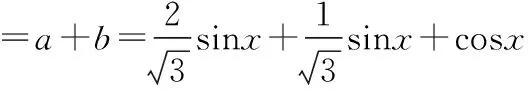

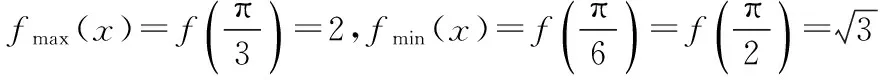
五、因找不到解题的着手点,解不下去


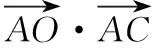

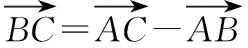
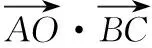
六、因思维变通性不够,解不下去