火箭垂直回收着陆段在线制导凸优化方法

张志国,马 英,耿光有,余梦伦

(北京宇航系统工程研究所,北京100076)

火箭垂直回收着陆段在线制导凸优化方法

张志国,马 英,耿光有,余梦伦

(北京宇航系统工程研究所,北京100076)

为了研究火箭垂直回收着陆段的制导律设计问题,通过求解最省燃料问题获得制导律,将连续优化问题转化为一类二阶锥凸优化问题(SOCP)。采用凸优化问题求解程序,实时计算最优轨迹获得当前制导周期内的制导律,导引火箭飞向目标点并垂直软着陆。该方法对着陆段初始状态偏差和下降过程中气动扰动有较强的适应性。进行了3个算例的仿真,结果表明:凸优化方法具有确定的收敛性质,相较于Radau伪谱法求解更加高效;参数设置简单,能够满足实时制导需求,具有在线应用的潜力。

火箭回收;垂直着陆;在线制导;凸优化

自20世纪60年代开始,世界各航天大国相继开展了大量可重复使用运载器研制工作,研究围绕着两条主线展开:一是以火箭发动机为动力的重复使用运载器,如航天飞机、X-37等;二是以吸气式发动机为动力,如X-30/NASP、高超声速巡航飞行器(HCV)等。从研究现状来看,火箭发动机技术相对比较成熟,已经成功应用于一次性运载火箭和部分重复使用的航天飞机上,同时两级部分重复使用运载器是目前研究发展的一个热点,Spacex公司的Falcon 9系列火箭已经多次成功实现一子级海上平台回收和陆上原场回收任务。

火箭垂直回收的制导控制方法是一项关键技术。以火箭一子级回收为例,返回任务可以分为[1]调姿段、减速转弯段、滑行段、动力减速段、气动减速段和垂直下降段。考虑到火箭着陆下降段时间短,精度要求高,因此对制导控制方法提出了更高的要求。

美国Apollo计划时期,已经有大量关于有动力着陆制导方法的研究,文献[2-3]给出了一种闭环形式的解,在月面着陆任务中,加速度采用时间的二次函数,该解析方法计算简单能够实时获得制导律[4],但整个过程无法对推力优化和限幅,若出现超出推力幅值的情况,将难以保证落点精度。随后的几十年间,多种数值和近似求解方法被提出。Najson[5]通过求解非最省燃料问题,给出了一种最优控制问题的近似解析解。Topcu[6]推导出有动力下降问题的一阶必要条件,并且表明燃料最优下降的推力控制律是Bang-Bang控制模式。Sostaric[7]采用Legendre伪谱法对定点着陆问题进行了数值求解。轨迹优化问题中的直接法在求解有动力软着陆问题中有一定的优势,将无限维的最优控制问题转化为有限维参数优化问题,可以通过非线性规划的方法进行求解。然而如果没有关于非线性规划求解程序收敛性质的显式信息,仅通过一般的迭代算法将无法满足实时在线制导律求解的要求。

近年来,Acikmese[8]和Blackmore[9]采用凸优化方法求解火星软着陆问题,为火箭有动力回收着陆段制导控制方法提供了新的途径。随后采用凸优化方法求解飞行器轨迹优化问题的研究逐渐增多,如行星软着陆问题[10]。Liu[11]采用凸优化方法研究了避免碰撞、非线性末端约束等复杂约束条件下的航天器交会和接近操作的轨迹优化问题。谭峰[12]将凸优化方法应用于高超声速飞行器轨迹跟踪控制。应用凸优化方法的关键是将问题构造成凸优化的结构。最好是能将参数优化问题构造成一类二阶锥凸优化问题(second order cone problem,SOCP[13])。二阶锥问题复杂程度低,并且可以在多项式时间内求解,目前原始对偶内点法(primal-dual interior point methods,IPM)已经能够完全求解SOCP,并且存在求解软件SeDuMi[14],YALMIP,MOSEK[15],CPLEX,SDPT3[16]等。凸优化问题的收敛精度可以指定为任意阶,并且达到指定精度的迭代程序,其迭代次数具有确定的上界。因此SOCP数值求解程序非常适合于在线计算和求解制导问题。

本文将凸优化方法应用到火箭有动力回收着陆段在线制导律的设计中,通过实时计算最优轨迹获得当前制导周期内的制导律,导引火箭飞向目标点并最终垂直着陆。凸优化方法具有确定的收敛性质,能够保证问题的收敛性和高效性。最后考察了该制导方法对于着陆点初始偏差和着陆过程中气动干扰的适应性。

1 火箭有动力着陆段动力学模型

首先建立着陆表面固定参考系。由于着陆段飞行距离较短,假设在整个着陆过程中地表为一个平面。如图1所示,rx方向垂直于着陆表面;ry方向为预先设定好的地表水平横向;rz方向满足右手坐标系,为地表水平侧向。假设火箭发动机的推力始终沿着箭体轴的方向,火箭飞行攻角在着陆段保持180°,火箭着陆段的动力学方程为[8]

(1)

式中:r(t),v(t)分别为火箭当前的位置和速度矢量;m(t)为火箭当前质量;Fc(t)为火箭的推力矢量;ge(t)为引力加速度矢量;Ispg0为发动机比冲,为简化后续推导过程的表达式,定义α=1/Ispg0为比冲的倒数,是一个常量;aD(t)为火箭在下降过程中受到的空气阻力加速度矢量,考虑到着陆段火箭飞行速度较低,气动阻力相对推力为小量级,因此首先将其当作扰动力进行分析。

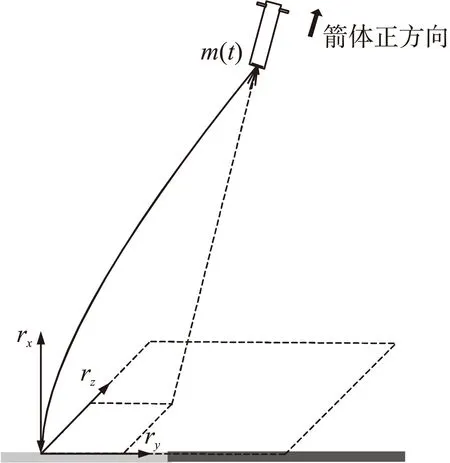
图1 火箭垂直软着陆下降示意图

在火箭下降的过程中,火箭制导系统需要根据当前状态和目标状态提供控制指令和关机指令,通过优化推力矢量Fc(t)的大小和方向,以最省燃料的方式实现火箭的精确定点着陆。根据飞行剩余质量计算公式:

(2)

由于Ispg0>0,因此在下降过程中最省燃料控制优化问题的目标函数为

(3)

式中:tf为火箭着陆过程的飞行时间,在应用制导算法前,可以通过轨迹优化方法给出tf的设计值,也可以利用经验公式进行估算。在下降过程中,火箭还需要满足各种约束条件。

①推力大小约束。

如果设计的制导控制律超过火箭自身控制能力的范围,将无法保证精确着陆的要求,因此优化设计过程中需要设置推力幅值约束,即

0≤F1≤‖Fc(t)‖≤F2, ∀t∈[0,tf]

(4)

式中:F1和F2分别代表推力幅值的下限和上限,在整个飞行时间内推力设计值不能超出范围。

②火箭与着陆点位置关系约束。

此约束主要包括两点。首先,需要保证火箭飞行过程中不能与地面相撞,即

rx(t)≥0, ∀t∈[0,tf]

(5)

(6)

③推进剂剩余量约束。

由于火箭在着陆段飞行之前已经历多个飞行阶段,剩余燃料有限,因此在着陆段进行制导律的设计时需要考虑推进剂剩余量的约束:

m(t0)=mwet,m(tf)≥mdry

(7)

式中:m(t0)为着陆阶段起始时刻的火箭质量;mwet为含燃料总质量;mdry代表燃料耗尽极限情况下火箭的结构质量,为火箭飞行过程中质量的下限。

④精确着陆约束。

火箭垂直回收最关键的任务是保证火箭最终能够精确定点着陆,即最终着陆瞬间的位置速度降为0:

r(0)=r0,v(0)=v0;r(tf)=0,v(tf)=0

(8)

式中:r0,v0分别为火箭着陆段的起始位置和速度;着陆末端约束保证位置r(tf)和速度v(tf)同时降为0。同时,火箭姿态需要保持垂直,由于推力方向沿着箭体轴的假设,最终推力方向垂直地面可以保证火箭姿态垂直着陆的条件,即加速度矢量的末端值需要满足在水平横向和侧向都为0,在竖直方向不为0,即

(9)

从上述优化问题模型中不难看出,存在质量随时间变化的非凸约束和最省燃料的非凸性能指标。若要采用凸优化方法进行求解,需要将原非凸问题进行凸化处理。

2 模型的凸化处理

在动力学方程(1)中,问题的非凸性质主要在于加速度右边项质量变量m(t)出现在分母中,可以通过取对数的形式转化为凸约束。原优化问题经过凸优化处理后得到的新问题与原问题优化结果的一致性可以参考文献[9]给出的证明,这里直接利用其证明结论。定义新的变量:

z(t)lnm(t)

(10)

对应地定义新的控制变量:

u(t)Fc(t)/m(t),σ(t)‖Fc(t)‖/m(t)

(11)

动力学方程可以写为

(12)

式中:z(t)为新定义的质量变量对数形式,u(t)和σ(t)为新定义的控制变量。相应地,推力幅值不等式约束变为

F1≤‖Fc(t)‖≤F2⟹F1e-z(t)≤σ(t)≤F2e-z(t)

(13)

对不等式约束两端进行Taylor展开,只保留一阶线性项:

(14)

新的不等式约束也定义了一个凸的可行域:

F1e-z0[1-(z(t)-z0(t))]≤σ(t)≤F2e-z0[1-(z(t)-z0(t))]

(15)

式中:z0为t时刻z(t)值的下确界,z0(t)=ln(mwet-αF2t),为了保证新定义的变量z(t)不违反原来的质量边界约束,定义新的约束:

ln(mwet-αF2t)≤z0(t)≤ln(mwet-αF1t)

(16)

火箭与着陆点位置关系角度约束方程(6)可以简写为

(17)

其他的约束都为线性或者凸约束,不需要进行额外处理,至此,原非凸优化约束和性能指标已经完成凸化处理,原连续优化问题转化为凸优化问题:

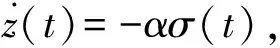
F1e-z0[1-(z(t)-z0(t))]≤σ(t),

σ(t)≤F2e-z0[1-(z(t)-z0(t))],

ln(mwet-αF2t)≤z(t)≤ln(mwet-αF1t),

rx(t)≥0, ‖Sx‖+cTx≤0, ∀t∈[0,tf],

(18)

3 着陆段制导模型及求解

通过时间等间隔离散,将原来的无限维优化问题转化为有限维的优化问题,在每个时间节点给出约束条件,采用数值程序求解离散问题。由于约束都是线性的或者二阶锥形式的,因此优化问题将是一个有限维的SOCP问题,可以通过文献[14]的程序快速求解。对于任意给定的时间区间[0,tf],均匀离散为N段,每段时间间隔为Δt,则对应离散节点的时间为

tk=kΔt,k=0,1,…,N

(19)

式中:NΔt=tf。然后通过M个离散点的控制量基函数来表示各离散时间节点的控制量u和σ:

(20)

式中:φ1,φ2,…,φM为M个离散点的控制量基函数,pj(tk)∈R4×1为待优化求解的常系数向量。基函数的选取有多种,可以选择简单常值函数,也可以选择插值多项式的形式,如果选择后者,则控制量的维数M可以远少于问题维数N(M≪N),这将能够明显减少SOCP问题的维数,减少问题求解的时间。选择不同的基函数,系数矩阵的定义也将不同,但是最优化问题的求解形式非常接近。因此,在这里将基函数选为分段常值函数,将最优控制问题转化为参数优化问题:

(21)

在各个时间节点处的微分方程的解和控制量可以通过下面的系数表示:

其中:

(22)

式中:x(tk)和η(tk)为离散时刻tk处的状态量和控制量矢量;I为单位矩阵。由于着陆下降段高度变化较小,重力加速度按照常值矢量处理:

ge(t)=(-9.806 65 0 0)T

(23)

对于气动加速度项,根据假设,火箭在飞行过程中攻角保持为180°,因此气动加速度方向为速度的反方向,由于着陆段飞行速度较小,气动阻力作为扰动力加入,后面将通过数值模拟考察该制导方法对气动阻力的适应性。至此,原来的连续优化问题完全转化成为有限维的凸优化问题:

(24)

对于离散点N的选取,随着N取值增大,达到同样的算法收敛精度,求解时间将变长,但是得到的制导律结果更加光滑,制导精度更高。一般N值选取需要兼顾制导精度和凸优化问题规模,对于本文研究的问题,当N<200时,离散问题规模小于5 000,可以保证单次求解燃料最优问题时间小于300 ms。上述模型(24)定义了有限维二阶锥问题,利用现有的SOCP求解程序可以在保证收敛的前提下非常高效地求解。

4 考虑气动力的制导模型

(25)

气动力项中,速度为时变量,加入问题离散矩阵中将改变状态空间矩阵A定常的性质,因此这里采用近似处理,在每一个离散时刻,速度幅值采用当前时刻速度v(tk)和终点速度0的平均速度‖v(tk)‖/2幅值。由于加入气动力,对应的状态空间矩阵需要进行修正:

(26)

式(26)与式(22)中的矩阵A表示相同的含义。除此之外,其他约束条件处理方法与第3节一致。

5 仿真算例

仿真算例选择Falcon 9 v1.2[17]发射600 km圆轨道,一子级回收返回原场任务,火箭气动减速段结束时刻位置、速度、质量作为着陆段制导状态量初始条件,其他结构参数(结构质量、发动机比冲)选择Falcon 9一子级结构参数,推力上限设为1台Merlin-1D发动机满推Fmax,下限设为0,即假设发动机具有连续任意大小可调节的推力,因此对于有动力下降段燃料最优问题,发动机只需要具备多次开关机功能即可实现。火箭飞行末端状态量与着陆点状态量一致。模拟着陆段制导律仿真参数设置如表1所示。

表1 火箭一子级着陆仿真参数表[17]

1)算例一。考察凸优化实时制导方法的求解效率。仿真过程中,每次求解凸优化问题获得一个制导周期内的制导律,火箭实时按照当前周期内制导律的引导,逐渐飞向目标着陆点。具体实现步骤如图2所示。

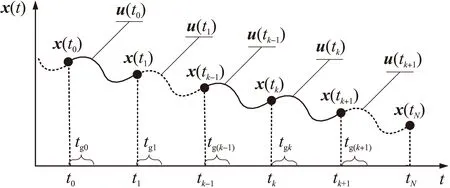
图2 凸优化制导方法过程图

①根据给定(预测)的火箭着陆段起始点位置x(t0),用凸优化方法求解x(t0)→x(tN)的制导律u(t0)。

②实际进入时段t0→t1内采用控制u(t0)。

③在第x(tk-1)处,采用上一时刻求解得到的u(tk-1)预测tk时刻的状态量x(tk),用凸优化方法求解x(tk)→x(tN)的制导律u(tk)。

④当火箭实际进入时段tk→tk+1内采用控制u(tk)。

⑤当飞行时刻到达tN时或经判断已实现着陆,结束制导指令。

采用本文设计的凸优化方法,整个仿真过程采用Matlab版本的凸优化求解工具箱SeDuMi 1.02进行凸优化问题的求解,得到仿真结果如图3～图8所示。作为对比,采用Radau伪谱法[18]求解同样的制导问题,得到对比仿真结果如图6～图8所示。

图4 凸优化制导着陆段一子级位置-时间变化曲线

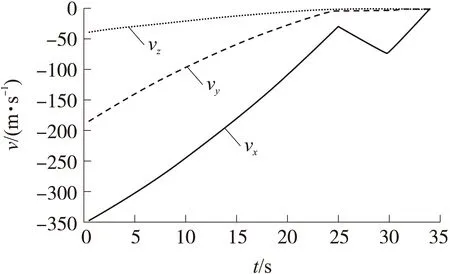
图5 凸优化制导着陆段一子级速度-时间变化曲线

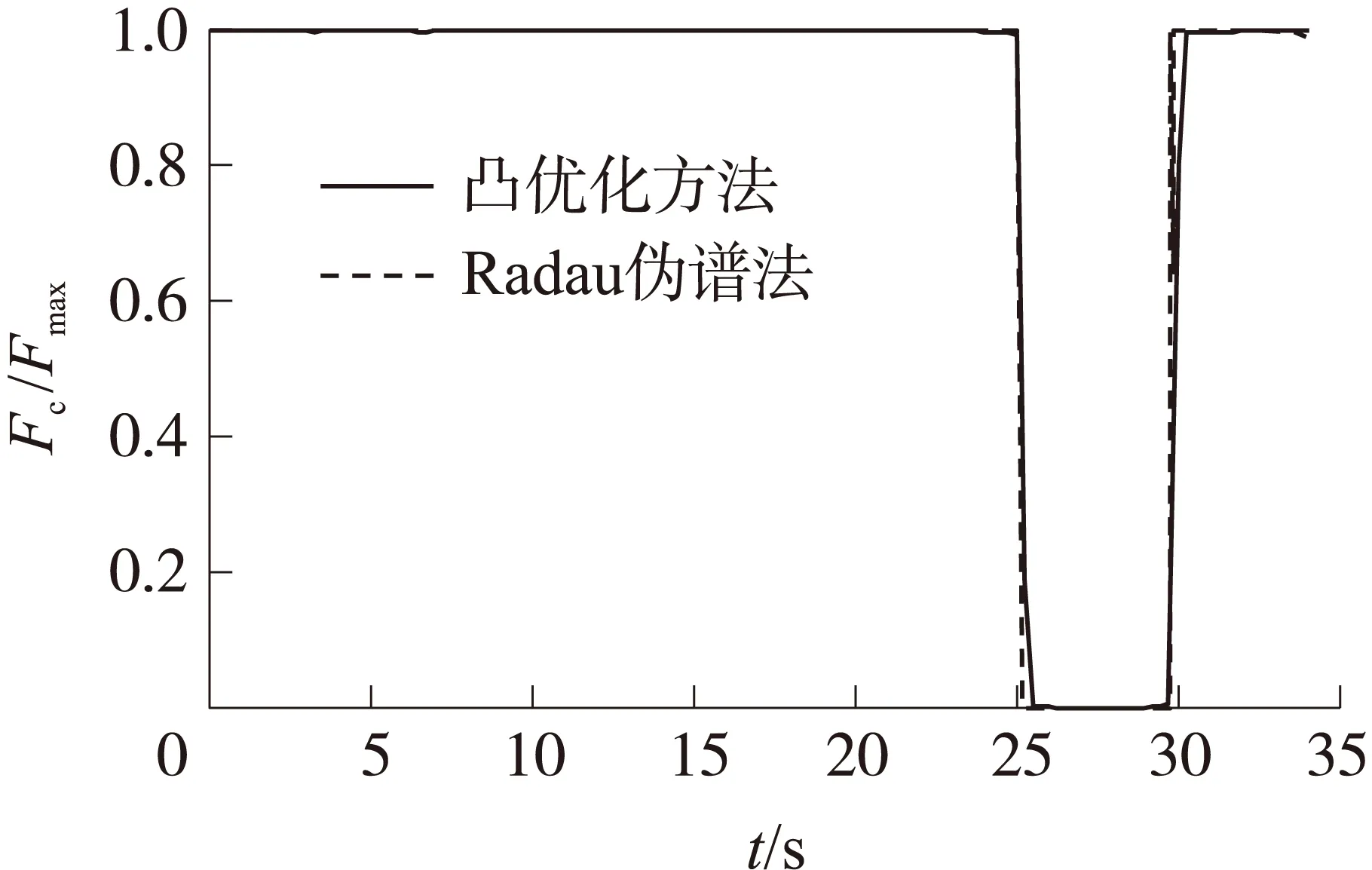
图6 着陆段火箭一子级推力幅值-时间变化曲线

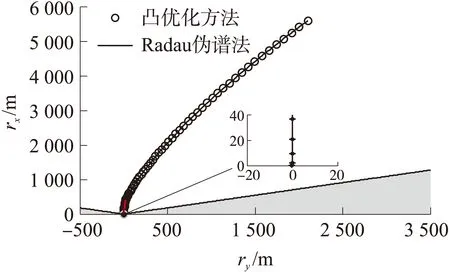
图7 着陆段火箭一子级水平横向距离-高度轨迹曲线

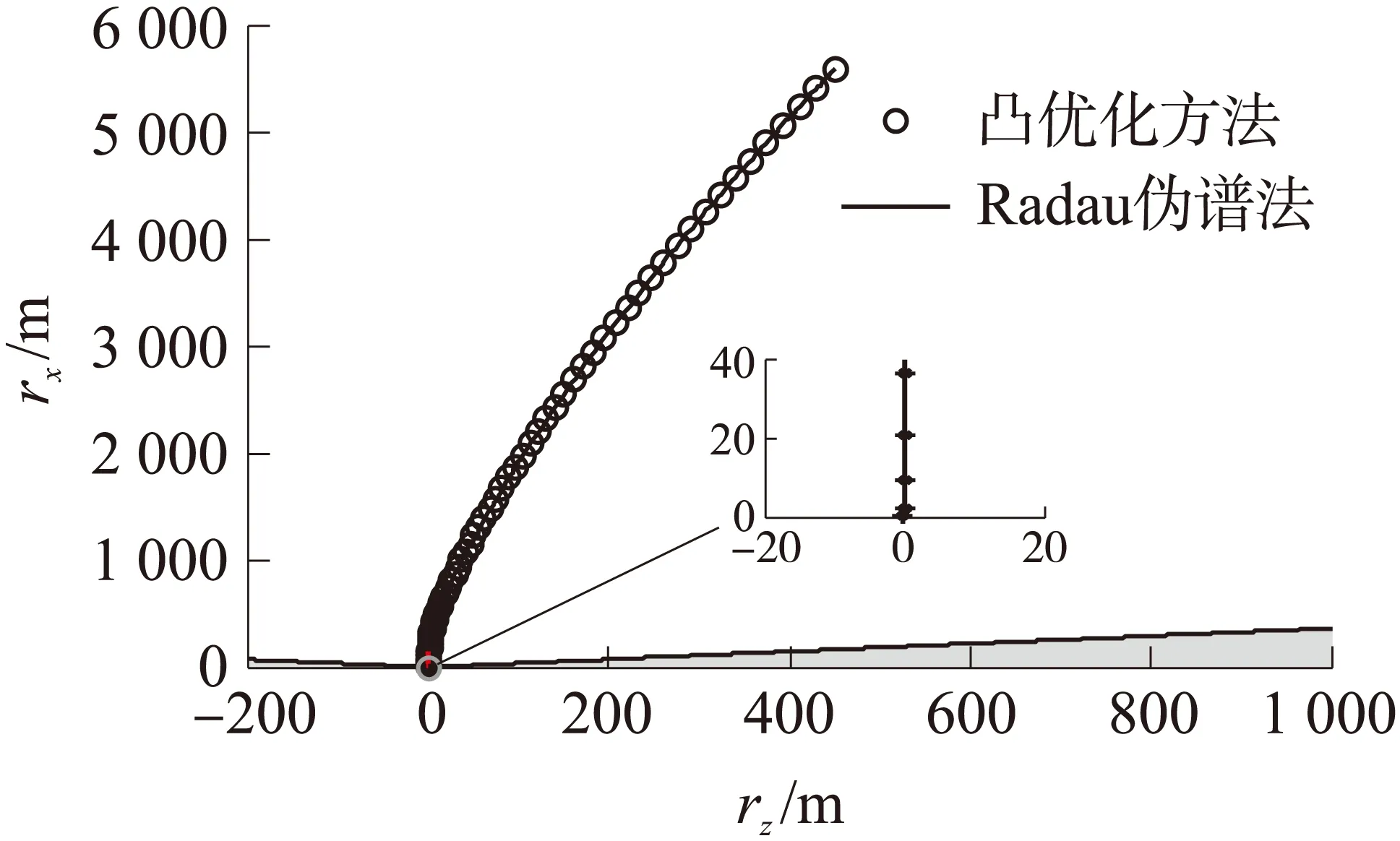
图8 着陆段火箭一子级水平侧向距离-高度轨迹曲线

从仿真结果曲线中可以看出,控制策略在每个制导周期内保持常值,如图3所示,能够导引火箭飞向着陆点,并在着陆瞬间仅有高度方向加速度ax,保证了垂直着陆的需求;着陆段终点位置如图4、速度如图5，在火箭飞行末端都降为0,实现了软着陆的目的;无论是从水平横向距离-高度曲线(图7),还是水平侧向距离-高度曲线(图8),火箭着陆时刻的姿态为垂直着陆(推力矢量方向分别为89.524 2°和89.263 9°);从图5中可以看出发动机的推力形式为典型的Bang-Bang控制,符合最优控制推力结果的一般规律,同时说明通过推力分档调节和姿态控制结合可以实现火箭垂直着陆并保证了推力幅值约束。

表2为凸优化方法与伪谱法制导效率的对比,表中,tp为2种方法分别求解轨迹优化问题获得制导律的单次平均计算时间,e为收敛精度,s为迭代次数。

表2 凸优化方法与伪谱法的制导效率对比表

整个仿真过程,凸优化方法制导周期选择为500 ms,单次制导律求解所需要的计算时间为200～300 ms(数值仿真过程采用台式机CPU3.19 GHz,内存1.93 GB,编程语言Matlab,算法收敛精度为1.0×10-9,凸优化原始与对偶问题的对偶间隙为1.0×10-15),而同样的基于Radau伪谱法的单步求解时间需要1 s以上。从计算效率角度对比,凸优化方法更适合应用于在线实时制导律的设计中。另一方面,伪谱法在求解轨迹优化问题时,需要给出过程中各状态量的范围区间,范围过大或者过小都会影响求解效果,甚至无法求解,而凸优化方法的设置则非常简单,只要将原问题转化为凸问题,无需其他设置,就能够实现快速求解,这些特点表明该方法具有一定的在线制导实用能力。

2)算例二。考察凸优化制导方法对着陆段起始状态偏差的适应性。火箭在大气减速阶段需要防止过载和热流过大,着重考虑力热约束,对制导控制精度允许一定范围的误差。大气减速阶段的终点误差将会导致着陆段起始状态的偏差,因此,着陆段制导方法应该对初始状态偏差具有一定的适应能力,即只要大气减速段能够将火箭的高度、速度降低到一定范围内,利用着陆制导方法都能保证最终的定点着陆精度要求。下面同时考虑高度rx、水平横向ry和水平侧向rz3个方向位置一定范围的初始偏差(各±20%和±50%),采用上述同样的方法进行制导律设计,加偏差仿真结果如表3所示。

表中:Δr0为着陆段起始点状态量相对于标准设计值的偏差;ηΔr0为其相对偏差;Δrf和Δvf分别为终点位置和速度的偏差量幅值。仿真结果如图9所示,着陆段凸优化制导方法的结果对于初值状态的偏差具有较强的适应性,即使初始偏差达到50%,在剩余燃料足够的条件下,该方法都能够有效地保证导引火箭垂直精确着陆于预定的着陆点,这就等价于气动减速段的末端约束可以进一步放宽,拓宽了火箭回收减速段的可设计范围。

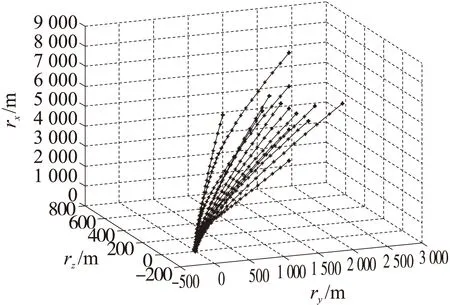
图9 不同初始状态偏差条件下的火箭着陆段三维飞行曲线

3)算例三。通过数值模拟来考察该制导方法对阻力的适应性。考察3种情况:算例3-1,制导过程采用忽略气动力模型;算例3-2,制导过程采用增加气动力修正模型;算例3-3,制导过程也采用增加气动力修正模型,同时rx和ry方向初始位置和速度大小在前面初值基础上降低50%。3个算例实际飞行都采用增加气动力全模型,制导周期仍为500 ms,ode45积分,仿真结果如表4所示。

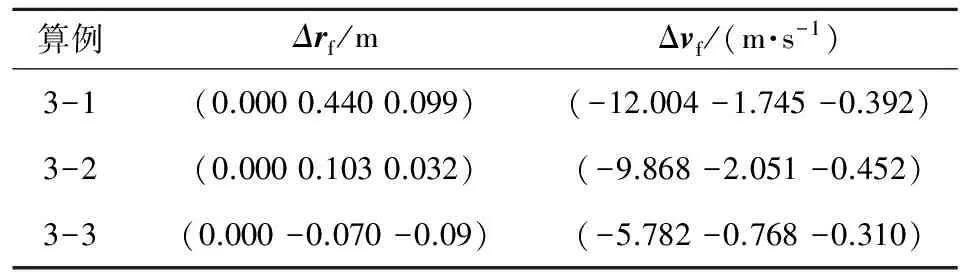
表4 考虑气动阻力的不同模型制导精度误差表

表4中,Δrf和Δvf分别为终点位置和速度的偏差量向量值。仿真结果如图10所示。图中,算例3-2曲线、算例3-1(a)曲线火箭下降初始位置和速度采用表1中的参数;算例3-3曲线、算例3-1(b)曲线火箭下降rx和ry方向的初始位置和速度大小在表1参数基础上降低50%。当竖直位移rx=0时积分终止。

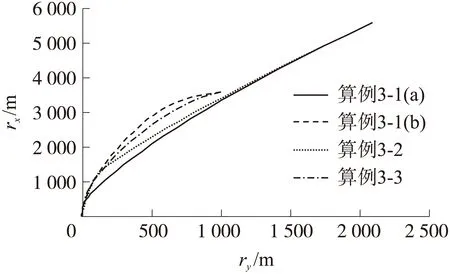
图10 增加气动力模型与原模型飞行轨迹对比图

经过增加气动力修正后的模型(算例3-2)能够保证在有气动力的条件下,火箭落点位置水平误差在0.1 m以内,速度纵向误差在10 m/s以内,速度水平误差在3 m/s以内。由于算例采取的初始纵向高度和速度较大,通过气动减速段让着陆段起点纵向速度进一步降低,可以保证最终火箭垂直着陆末端纵向速度误差进一步减低到6 m/s以内(算例3-3)。在实际工程中,该速度可以通过增加缓冲机构实现软着陆的要求,表明本文设计的凸优化制导方法已经可以使火箭在有气动力的条件下具有定点垂直精确着陆的应用潜力。

6 结束语

本文设计的火箭垂直回收着陆段凸优化制导方法,能够在满足各种约束条件下,以最省燃料的方式导引火箭一子级精确定点着陆。原优化问题转化为SOCP问题,利用凸优化求解程序能够在多项式时间内实现任意阶求解精度,保证较高的求解效率,并且该制导算法设置简单,具有在线应用的潜质。后续研究可以考虑建立更加精确的气动力模型,并加入地球自转对落点位置的影响,来满足更高精度制导律的设计需求。

[1] 高朝辉,张普卓,刘宇,等.垂直返回重复使用运载火箭技术分析[J].宇航学报,2016,37(2):145-152. GAO Zhao-hui,ZHANG Pu-zhuo,LIU Yu,et al.Analysis of vertical landing technique in reusable launch vehicle[J].Journal of Astronautics,2016,37(2):145-152.(in Chinese)

[2] MEDITCH J S.On the problem of optimal thrust programming for a lunar soft landing[J].IEEE Transactions on Automatic Control,1964,9(4):477-484.

[3] MIELE A.The calculus of variations in applied aerodynamics and flight mechanics[J].Mathematics in Science & Engineering,1962,5:99-170.

[4] KLUMPP A R.Apollo lunar descent guidance[J].Automatica,1974,10(2):133-146.

[5] NAJSON F,MEASE K.A computationally nonexpensive guidance algorithm for fuel efficient soft landing:AIAA 2005-6289[R].San Francisco,CA:AIAA,2005.

[6] TOPCU U,CASOLIVA J,MEASE K.Fuel efficient powered descent guidance for mars landing:AIAA 2005-6286[R].San Francisco,CA:AIAA,2005.

[7] SOSTARIC R,REA J.Powered descent guidance methods for the moon and mars:AIAA 2005-6287[R].San Francisco,CA:AIAA,2005.

[8] ACIKMESE B,PLOEN S R.Convex programming approach to powered descent guidance for mars landing[J].Journal of Guidance Control & Dynamics,2007,30(5):1 353-1 366.

[9] BLACKMORE L,ACIKMESE B,SCHARF D P.Minimum landing error powered descent guidance for mars landing using convex optimization[J].Journal of Guidance Control & Dynamics,2010,33(4):1 161-1 171.

[10] ACIKMESE B,CARSON J M,BLACKMORE L.Lossless convexification of nonconvex control bound and pointing constraints in the soft landing optimal control problem[J].IEEE Transactions on Control Systems Technology,2013,21(6):2104-2113.

[11] LIU X.Autonomous trajectory planning by convex optimization[D].Iowa:Iowa State University,2013.

[12] 谭峰,陈洪普,侯明哲,等.高超声速再入飞行器基于凸优化的模型预测轨迹跟踪控制[C]//第32届中国控制会议.西安:中国自动化学会,2013:4 167-4 171. TAN Feng,CHEN Hong-pu,HOU Ming-zhe,et al.Model predictive trajectory tracking of a reentry hypersonic vehicle based on convex optimization[C]//Proceedings of the 32nd Chinese Control Confernce.Xi’an:Chinese Association of Automation,2013:4 167-4 171.(in Chinese)

[13] 王书宁,许鋆,黄晓霖,等.凸优化[M],北京:清华大学出版社,2013. WANG Shu-ning,XU Yun,HUANG Xiao-lin,et al.Convex optimization[M].Beijing:Tsinghua University Press,2013.(in Chinese)

[14] STURM J F.Using SeDuMi 1.02,a MATLAB toolbox for optimization over symmetric cons[J].Optimization Methods & Software,1999,1(11/12):625-653.

[15] ANDERSEN E D,ROOS C,TERLAKY T.On imple-menting a primal-dual interior-point method for conic quadratic optimization[J].Mathematical Programming,2003,95(2):249-277.

[16] TOH K C,TODD M J,TÜTÜNCÜ R H.SDPT3:a Matlab software package for semidefinite programming,Version 1.3[J].Optimization Methods & Software,1999,11(1):545-581.

[17] Space Exploration Technologies Corp.Falcon 9 launch vehicle payload user’s guide,rev 2[EB/OL],2015-10-21/2016-10-21.http://www.spacex.com/sites/spacex/files/falcon_9_users_guide_rev_2.0.pdf.

[18] RAO A V,BENSON D A,DARBY C,et al.Corrigendum Algorithm 902:GPOPS,a MATLAB software for solving multiple-phase optimal control problems using the gauss pseudospectral method[J].Acm Transactions on Mathematical Software,2010,37(2):163-172.

Convex Optimization Method Used in the Landing-phase On-line Guidance of Rocket Vertical Recovery

ZHANG Zhi-guo,MA Ying,GENG Guang-you,YU Meng-lun

(Beijing Institute of Aerospace System Engineering,Beijing 100076,China)

To study the guidance law for vertical-recovery landing phase of rocket,the guidance law was obtained by solving the problem of saving most fuel.The continuous optimization problem was transformed into a second-order cone program(SOCP)convex optimization problem.During each guidance-period,the guidance law was obtained by calculating the optimal trajectory to guide the rocket to the preassigned target and achieve vertical soft landing.The method has strong adaptability to the initial state variables deviation and aerodynamic disturbance during descending.The simulation of three examples was carried out.The results show that the convex optimization method has deterministic convergence properties,and it is an efficient solving method compared with Radau pseudo-spectrum method.The setting of parameters by the method is easy,and it meets real-time guidance requirement and can be implemented for on-line application.

rocket recovery;vertical landing;on-line guidance;convex optimization

2016-10-24

张志国(1991- ),男,博士研究生,研究方向为航天器动力学,导航、制导与控制。E-mail:zhangzhiguo08@yeah.net。

V448.13

A

1004-499X(2017)01-0009-08