制导炮弹可控滚转执行机构模型分析

刘源翔,崔 岩,李 睿,葛立坤

(中国北方车辆研究所 总体技术部,北京 100072)

制导炮弹可控滚转执行机构模型分析

刘源翔,崔 岩,李 睿,葛立坤

(中国北方车辆研究所 总体技术部,北京 100072)

为解决可控滚转电动舵机在低旋尾翼弹上的应用,以舵体为研究对象,分析了作用在舵体上的力矩,建立了系统动力学模型;在分析舵机结构的基础上建立了舵机机构的的动力学模型和系统动力学模型。在不同的工况条件下对系统模型进行了分析和验证,分析结果验证了系统动力学模型的正确性。仿真结果表明,该舵机降低了伺服电机功率及响应速度的要求,提高了舵面效率,为在低旋制导炮弹上的应用提供了一种新的解决方案及理论参考。

制导炮弹;可控滚转舵机;电动舵机;动力学模型

目前,对于低旋制导炮弹的控制大多采用鸭舵控制、脉冲矢量控制及弹头修正[1]等简易制导控制技术。文献[2]较为全面地介绍了不同类型弹道修正执行机构,并分析了各自的工作原理及优缺点。文献[3]设计了一种弹道修正引信电动舵机并仿真验证了其可行性。文献[4-5]探讨了采用脉冲发动机直接进行质心控制的方案,但是脉冲发动机修正力有限,安装位置苛刻以及喷流对弹的气动特性有很大的影响。文献[6]提出一种新型的四轴联动舵机,通过一个舵机实现4片舵翼的同时控制,在一定程度上降低了舵机输出功率,并没有提高舵片的偏转速度和效率。针对制导炮弹舵机控制效率较低的问题,文献[7]提出了一类可应用于旋转弹控制的可控滚转舵执行机构,提高了舵机的舵面效率,并降低对伺服电机功率及响应速度的需求,但只对舵系统的滚转控制原理做了初步的研究,尚未对系统动力学模型做进一步的分析和讨论。

1 舵系统结构和原理

可控滚转舵系统可以相对于弹体自由滚转,通过控制舵机舱的滚转,调整导弹的最大升力面,减小通道间的耦合[5]。可控滚转舵系统的鸭式布局示意图如图1所示,系统采用单通道控制方式,舵机舱可以由机构保证与弹体相对自由滚转,系统的2个舵翼由2个独立的电机控制,其工作原理在文献[7]中已经有详细的论述。

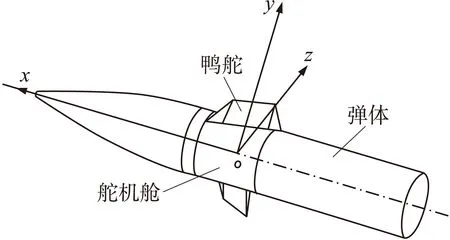
图1 可控滚转舵系统鸭式布局

对于传统的旋转弹执行机构,弹体旋转一周,在从0°～360°的任一方向上均可出现一次向该方向提供控制力的机会,舵翼提供给弹体等效周期控制力实现对弹道的修正。而可控滚转执行机构可以在任意时刻任意方位上实现对弹体的控制,在系统滚转角指令不变时,舵机舱相对于准弹体坐标系的滚转角稳定,此时舵机舱以弹体的滚转速度反向滚转。如果已知弹体的偏离方位,需要改变滚转角时,两片舵片作差动,产生副翼作用,调整舵机舱的滚转速度,以此调整滚转角。当滚转角稳定后,利用差动舵产生的控制力抵消摩擦力矩,以维持相对弹体坐标系转动,并在此过程中完成在此方向上的舵片偏转,实现弹体向该方向的机动。为了实现上述过程,采用如图2所示的舵偏角控制执行机构。

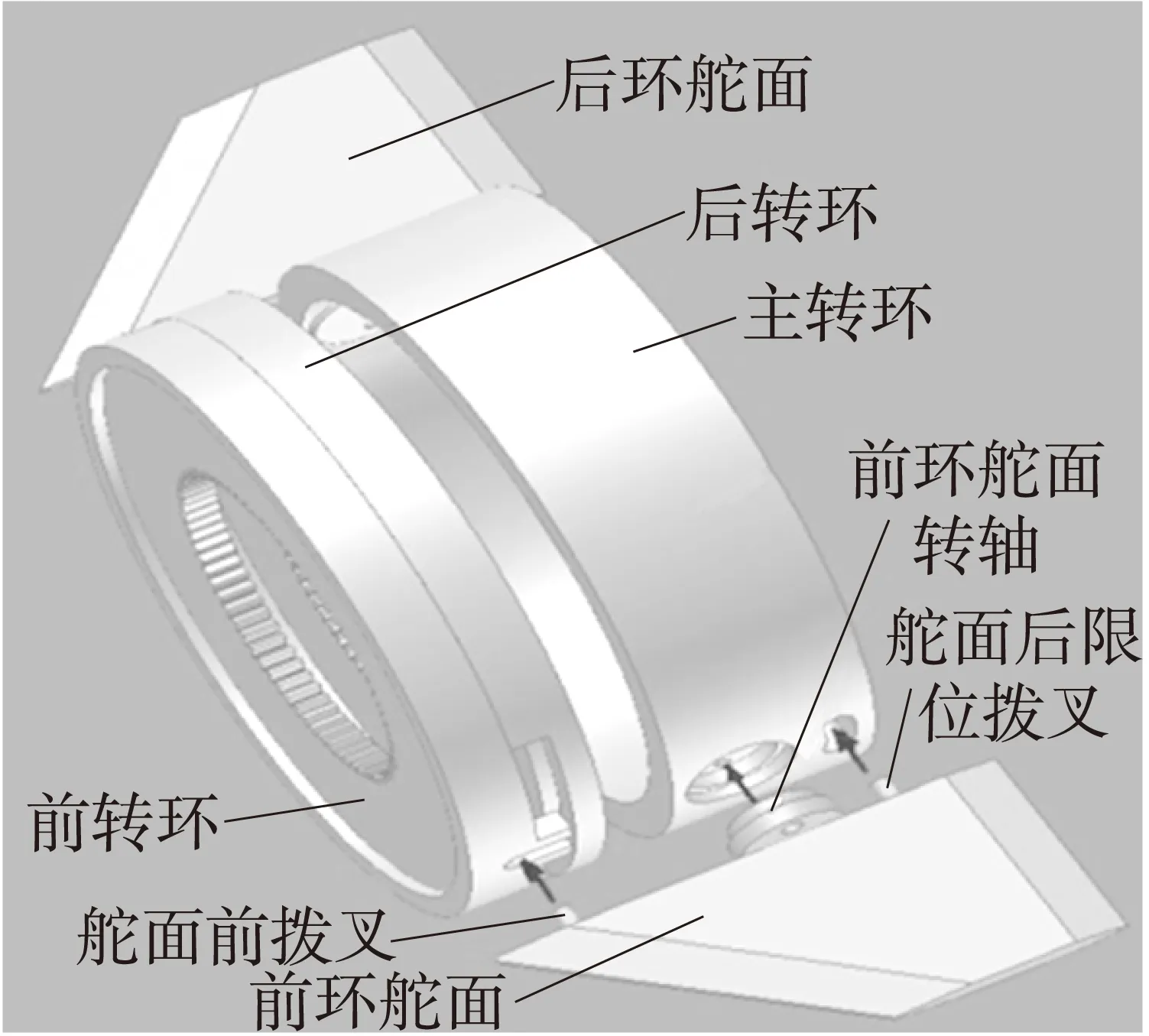
图2 舵偏角控制执行机构

该系统舵偏角是通过主转环与前、后转环的运动差产生的。主转环的空间位置实际上就是舵机的方位角,通过前、后转环的运动,产生舵偏角。舵偏角在空气动力的作用下,推动主转环运动,达到对方位角的调整。

显然,该系统主要依靠空气动力维持滚转角的稳定,大大降低了对电机功率的需求;舵机一直处于工作状态,提高了系统的响应速度;当舵系统滚转角稳定后,旋转导弹可以使用倾斜转弯(BTT)控制方式提高其机动性能。

2 可控滚转舵系统模型分析

2.1 舵机动力学模型分析

舵偏角定义为舵面与舵轴所在的弹体横对称面的夹角,顺时针为正。如图3所示,前转环运动形成的舵偏角为δ1,后转环运动形成的舵偏角为δ2,此时舵偏角为正,速度v方向表示来流方向。

图3 舵偏角示意图

定义等效舵偏角δD和等效副翼偏角δF分别为

(1)

(2)

以舵体为研究对象,作用在舵体上的力矩包括:由副翼作用引起的空气动力矩MF和由舵体与弹体的相对运动引起的摩擦阻尼力矩MV,其分别为

警察高校实验教学教师既是专业知识的传授者，又是道德言行的引导者。要把立德树人转化为内心信念，把崇高师德内化为自觉价值追求。要健全师德师风评价体系，完善师德建设制度规范，实行“师德一票否决制”。引导教师坚持教书和育人相统一，坚持言传和身教相统一，坚持潜心问道和关注警务实践相统一。以德立身、以德立学、以德施教。

(3)

(4)

根据上述定义,准弹体坐标系下舵体滚转运动的动力学方程为

(5)

(6)

式中:s为传递函数算子。舵机舱滚转模型如图4所示,图中,τ3为转环转动角度到舵片偏转角度的减速比。

图4 舵机舱滚转模型框图

由此可得等效副翼偏角对弹体滚转角的传递函数:

(7)

同理,弹体滚转角速度对舵体滚转角的扰动传递函数为

(8)

2.2 舵机结构模型分析

根据上述分析,建立整个机械机构的动力学及运动学部分的系统框图,如图5所示,图中忽略了由于非线性引起的转速。图中,GNL表示结构限位的非线性模型部分,n1和n2为2个电机的转速,τ1和τ2为减速机构的减速比,τ3为前(后)转环到舵面偏角的减速比。

图5 系统机械结构模型系统框图

等效副翼偏角δF、等效舵偏角δD的传递函数表示为

(9)

舵机舱滚转方位角与等效副翼偏角的关系表达式为

(10)

将式(9)代入式(10),整理可得:

(11)

(12)

式中:n=(n1+n2)/2,为电机的基准转速,即稳态时电机具有一定的基准转速,转速的大小与系统的减速比和弹体的滚转速度有关。

系统中伺服电机模型简化为

(13)

式中:km为电机的转矩常数,Tm为电机机电时间常数,u1和u2为副翼控制指令。

理想条件下,副翼作用时令u1=u2=u,可得舵机舱滚转方位角传递函数:

(14)

系统扰动传递函数:

(15)

3 模型验证与分析

3.1 不同条件下的模型验证

根据上述建立的系统模型,验证舵机在不同条件下该系统模型的正确性。

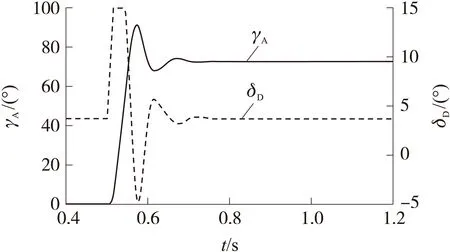
图时方位角及舵偏角响应曲线

此时导弹相当于不滚转弹,到达目标方位角后,由于弹体不滚转,舵面在方位角稳定后将稳定在零位。仿真结果如图7所示。

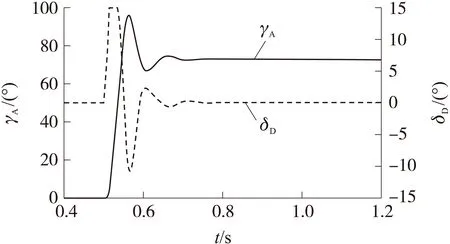
图时方位角及舵偏角响应曲线

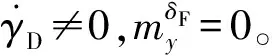
此时无空气动力矩作用,与地面模拟试验条件相同,舵机完全依靠前(后)转环拖动主转环运动,舵翼处于结构限位条件下,方位角稳定时,电机一直处于恒速转动状态。仿真结果如图8所示。

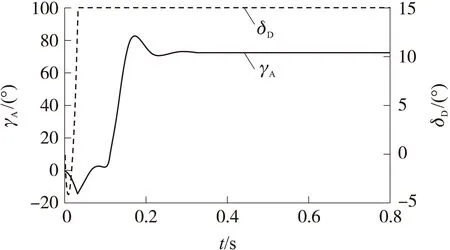
图时方位角及舵偏角响应曲线

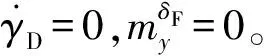
此时,无空气动力矩作用且弹体不滚转,舵机完全依靠前(后)转环拖动主转环运动,舵翼处于结构限位条件下,方位角稳定时,电机转速为0。仿真结果如图9所示。

图时方位角及舵偏角响应曲线

条件③和条件④时,电机工作状态的仿真结果如图10所示。

图10 电机转速曲线

3.2 仿真结果分析

将图7与图6对比可知,在弹体不滚转时,系统方位角的超调量更大;在方位角稳定上,弹体不滚转条件下的舵偏角更小,且稳态时舵翼的稳态角度为0;而弹体滚转时,稳态的舵翼角度不为0,因为此时需要提供副翼作用抵消弹体的滚转,保持方位角的稳定。

综上所述,对于该可控滚转电动舵机,在有空气动力矩作用下,系统的响应时间会变快,系统的超调量也相对较大,在弹体滚转条件下,方位角稳定时,系统的舵偏角不为0。伺服电机的稳态转速也不为0;在没有空气动力矩作用时,方位角的变化完全依靠结构的限位,由伺服电机驱动前(后)转环拖动运动。当弹体滚转条件下,方位角稳定时,系统的舵偏角为满舵偏,伺服电机的稳态转速也不为0。上面的仿真结果也充分验证了这一点,说明系统的模型是正确的。

4 结论

本文通过对可控滚转舵系统结构组成原理及工作原理进一步分析和研究,建立了舵机的结构和动力学模型,并通过仿真验证了舵机在不同工作条件下模型的正确性,为此类舵机在旋转导弹上的应用提供了参考。

[1] 王毅,宋卫东,佟德飞.固定鸭舵式弹道修正弹二体系建模[J].弹道学报,2014,26(4):36-41. WANG Yi,SONG Wei-dong,TONG De-fei.Modeling of two-rigid-body system for trajectory correction projectile with fixed-canard[J].Journal of Ballistics,2014,26(4):36-41.(in Chinese)

[2] 张冬旭,姚晓先,郭致远.弹道修正机构综述[J].导航定位与授时,2014,1(2):39-45. ZHANG Dong-xu,YAO Xiao-xian,GUO Zhi-yuan.Overview of the correction mechanism on two-dimensional trajectory correction projectile[J].Navigation Positioning & Timing,2014,1(2):39-45.(in Chinese)

[3] 李虎全,李世义,罗会甫.弹道修正引信用电动舵机设计与仿真[J].微计算机信息,2009(7):13-15. LI Hu-quan,LI Shi-yi,LUO Hui-pu.Design and simulation study of trajectory correction fuze electromechanical actuator[J].Microcomputer Information,2009(7):13-15.(in Chinese)

[4] WEY P.Performance analysis of ISL’s guided projectile[C]//23rd International Symposium on Ballistics.Tarragona,Spain:IBC,2007:655-663.

[5] 姚文进,王晓鸣,高旭东,等.弹道修正弹脉冲修正机构简易控制方法[J].弹道学报,2007,19(3):19-22. YAO Wen-jin,WANG Xiao-ming,GAO Xu-dong,et al.A simple control method for impulse correction device in trajectory correction projection[J].Journal of Ballistics,2007,19(3):19-22.(in Chinese)

[6] 王俊全,王晓鸣,李文彬.新型四轴联动舵机的原理和动力学分析[J].兵工学报,2006,27(1):54-57. WANG Jun-quan,WANG Xiao-ming,LI Wen-bin.The principle and dynamics analysis of a four-shaft-linked actuator[J].Acta Armamentarii,2006,27(1):54-57.(in Chinese)

[7] 程建伟,于志远,姚晓先,等.可控滚转舵系统滚转控制研究[J].北京理工大学学报,2010,30(6):670-673. CHENG Jian-wei,YU Zhi-yuan,YAO Xiao-xian,et al.Study of rolling control for a controllable-rolling actuator system[J].Transactions of Beijing Institute of Technology,2010,30(6):670-673.(in Chinese)

Modeling and Analysis of Controllable-rolling Actuactor System

LIU Yuan-xiang,CUI Yan,LI Rui,GE Li-kun

(General Technical Department,China North Vehicle Research Institute,Beijing 100072,China)

In order to study the application of controllable-rolling actuactor(CRA)on finned projectile,the actuator was taken as study object.The moment acting on actuator was analyzed,and the system dynamics model was built.The structure of actuator was analyzed,and the dynamic model of actuator and the dynamics model of system were built.The system model under different condition was analyzed and verified.The result indicates that the dynamic model of the system is correct.The requirement of power and response speed of servo motor are reduced by the actuator,and the rudder wings efficiency is improved.The study offers solution and theory for the application of actuator on the guided projectile.

guided projectile;controllable-rolling actuator;electromechanical actuator;dynamic model

2016-09-06

刘源翔(1986- ),男,工程师,研究方向为履带车辆总体设计。E-mail:liuxiangningxiang@126.com。

TJ765.2

A

1004-499X(2017)01-0017-05