随动系统的参考模型自适应模糊控制器设计

雷 昱,巫亚强,周 杨,舒立鹏

(西北机电工程研究所，陕西 咸阳 712099)

随动系统的参考模型自适应模糊控制器设计

雷 昱,巫亚强,周 杨,舒立鹏

(西北机电工程研究所，陕西 咸阳 712099)

常规模糊控制器对系统的控制方式完全基于启发式的控制，对超调量的回调速度较慢。以武器随动系统和模糊控制为背景，提出一种基于参考模型的自适应模糊控制器以改善其控制性能。利用参考模型与系统过程的递归方程式的关系，确定自适应模糊控制器的单点输出值，从而克服启发式控制方式在小误差范围内灵敏度差的缺点，达到加快系统的过渡时间和增强系统的速度跟踪性能的目的，最终使设计的控制器对武器随动系统的控制效果达到其技术指标的要求。仿真结果验证了所设计的控制策略的有效性。

永磁同步电机；模糊控制器；模糊论域；参考模型；自适应算法

以某型高炮为对象，采用模糊控制器作为其位置环，研究其对于炮身高低角度的调转性能。常规的模糊控制器其控制方式完全基于模糊控制表和模糊控制规则的启发式控制，这种方式实现简单，但不具备“记忆”功能，在系统参数变化时系统动态性能也发生改变[1]。为了改善常规模糊控制器的性能，研究了基于参考模型的自适应模糊控制器，通过原理分析和Simlink仿真说明其优于常规模糊控制器的控制性能，最终达到满足某型高炮战技指标的目的。

1 系统位置环设计

1.1 常规模糊控制器的设计

模糊控制器的设计有以下几个重要环节：模糊控制器的维数选择、语言变量的选择、隶属度函数的确定、制定模糊规则表和模糊控制器规则、量化因子的选定及解模糊方法等的选择。

模糊控制器维数：所谓维数就是指模糊控制器的输入的单位个数，笔者采用二维设计，即考虑了系统误差和误差变化速度。

语言变量：语言变量可选择3、5、7、9个语言值，显然语言值越多控制效果越细腻，但计算量也随之增高，所以选择合适的语言变量数目是至关重要的。笔者选择5个语言值的设计：“负大、负小、零、正小、正大”。

隶属度函数：本文选择三角形隶属度函数，其优点是斜率一定，且顶点明显，即隶属度的变化速度恒定。

模糊控制规则：采用传统的“if-then”规则，这种方法也称经验归纳法。

量化因子：量化因子对模糊控制系统的动、静态性能有较大的影响。常规模糊控制器量化因子的确定方法是按照控制量的实际变化范围和其模糊论域范围的映射关系确定：

(1)

式中：k为量化因子；M为控制量的实际范围；m为控制量的模糊论域范围。

解模糊方法：选用总和重心解模糊方法，此方法避免了在某些情况下模糊控制规则将输出的权重分配给不重要的模糊规则。

模糊控制表：选择二维五语言变量，所以模糊控制表为52条模糊规则，具体如表1所示。

表1 转速n模糊控制表

模糊论域：根据速度环的实际输入确定位置环控制器输出的模糊论域范围，设置为[-128,128]。通过输出量化因子kn量化达到电机额定转速。

而输入量化因子ke的论域根据某型高炮战技指标要求的1 400密位设计，故其模糊论域设置为[-2 048,2 047]。

kΔe是误差对于时间的微分，按照二阶系统的上升曲线，估计其模糊论域的范围设置为[-1 166,1 166]。

模糊控制器的总输出应该是电机额定转速，而速度环输入的单位是rad/s，并在控制器输出位置设置限幅模块，上下限为[-315,315]。根据式(1)计算得ke=1.46，kΔe=1.75，kn=2.46。

1.2 机械传动部分设计

电机额定转速为3 000 r/min，而某型高炮的炮身高低调转速度为70 (°)/s，本文只涉及高低系统的机械传动，方位系统可以类似得出。计算高低系统减速比：

(2)

速度环输出值单位为r/min，而某型高炮的战技指标要求的单位为密位，所以其模型需要涉及单位的转换，其模型如图1所示。

图1中速度环输出Ω的单位为rad/s，首先乘以30/π，将单位转换为r/min，再除以式(2)求出的减速比，可以得到负载侧的转速，之后乘以100，将单位转换为密位/s，最后对其积分得出的值为位置环输出θ，单位为密位。位置环输出θ反馈回主令位置的输入点做差值计算，便得到主令误差，从而通过位置环控制器对其进行控制[2]。

1.3 常规模糊控制器仿真

系统动态结构图如图2所示。

由图2可得出某型高炮驱动器闭环传递函数，略去三次项[3]后为

(3)

图2中Ms为某型高炮的身管静阻力矩折算到电机轴侧，J为身管转动惯量折算到电机轴侧与电机转子转动惯量之和。

阶跃信号的跟踪性能可以反映整个系统的滞后时间，所以用阶跃信号仿真炮身定位调转最合适；正弦信号的跟踪性能可以反映系统对于速度的跟踪性能，本文只研究某型高炮的高低角度调转，因其高角最大值为1 400密位，故正弦信号的单振幅A设置为700密位，正弦频率设为1rad/s。周期公式为

(4)

式中：ω为运动圆频率；Ω为跟踪速度；ε为跟踪加速度。

系统的采样时间对应系统的延时大小，即PWM载波周期，本文为0.25 ms[4]。仿真时间分别为5 s和14 s。

仿真结果如图3～5所示。从仿真结果看，常规模糊控制器在大范围调转时，峰值时间2.1 s，但过渡过程太长，主要由于启发式控制方式在小误差范围内灵敏度太低。正弦跟踪误差最小为±5密位左右。

2 模型参考自适应模糊控制器设计

2.1 自适应系统的原理及结构设计

常规模糊控制器的控制精度不能满足要求，需对其性能进行改善。设计了一种自适应模糊控制器，其结构图如图6所示。

由图6可知，需要将参考模型的输出与系统的过程输出做差值，将差值大小送入自适应算法，根据系统当前时刻的位置与参考模型当前时刻的位置差距，自适应算法计算出校正值，与位置环控制器做相乘运算补偿或衰减电机转速最终使负载的位置与参考模型在同一时刻保持相似。

图6中参考模型采用二阶数学模型，直接指定其峰值时间和超调量，计算其阻尼系数和自然角频率为

(5)

(6)

式中：ξ为阻尼系数；ωn为自然角频率；tm为峰值时间；σ为超调量[5]。

从而得出这个参考模型的具体传递函数为

(7)

由于系统需要自适应的是参考模型的稳态阶段，所以需要根据图3的仿真结果指定系统超调量和峰值时间，超调量指定为0.8%。将峰值时间指定为2.1 s时，参考模型动态曲线在2.4 s时可以进入稳态。带入式(7)可得：

(8)

系统过程的传递函数由图3仿真结果得出，峰值时间2.1 s，超调量0.64%。带入式(7)可得：

(9)

两者都是在连续时间域上的传递函数，对两者分别做Z变换，将连续时间域转换为离散频率域，采样间隔为PWM的基波频率，为20 ms。转换结果为

(10)

(11)

两者在离散域上的输出表达为

yM(k)=aM1yM(k-1)+aM2yM(k-2)+bMθr(k-1)

(12)

ys(k)=as1ys(k-1)+as2ys(k-2)+bsθr(k-1)

(13)

由式(10)、(11)可知，aM1=1.113，aM2=-0.178,bM=0.042，as1=1.078,as2=-0.149,bs=0.046。将这些值代入式(12)、(13)可得参考模型和系统过程的递归方程式：

yM(k)=1.113yM(k-1)-0.178yM(k-2)+

0.042θr(k-1)

(14)

ys(k)=1.078ys(k-1)-0.149ys(k-2)+

0.046θr(k-1)

(15)

2.2 自适应控制器的设计

自适应算法控制器选用二维七语言值的模糊控制器，两输入分别为eM和ΔeM，即参考模型和系统过程的误差与误差的变化率。但它不同于常规模糊控制器的启发式控制方法，而是根据其单点输出式，得到其在离散域上的单点输出方式，计算出其模糊控制表的所有输出单点值，作为自适应算法的具体输出数值。其模糊论域的归一化分布如图7所示。

如图7所示，自适应控制器的两输入量的模糊论域完全一致，其分布是关于零模糊集合的对称，这样的隶属函数交叠方式可以确保最多由4条控制规则对模糊控制器的精确输出有贡献。最外侧的语言值跨度较大主要是考虑eM或ΔeM过大时可以输出较大的校正力或自适应力，从而快速缩小误差。在最内侧设置了零模糊集合为梯形，这相当于定义了一个零区，以保证在稳态或接近稳态时自适应算法不会被激活。

自适应模糊控制器的输出单点式如下：

uFC=k1ce,i+k2cΔe,j=Aq

(16)

式中：uFC为模糊控制器的输出；k1、k2分别为控制器系数；ce为误差输入的模糊隶属函数重心；cΔe为误差变化率的模糊隶属函数中心；下标i、j分别表示两变量的语言值次序(i、j=1,2，…，7);Aq为单点输出的具体值。

由参考模型和系统过程的递归方程式可以看出，两者均存在前一时刻的输入，这相当于模糊控制器的前馈部分[6]：

uFF(k)=k3θr(k)

(17)

控制器系数k值的确定方法如下[5]：

(18)

(19)

(20)

将式(12)、(13)计算所得的系数代入，可得k1=-0.131，k2=-0.372，k3=0.048，带入式(16)、(17)中，得到：

uFC=-0.131ce,i-0.372cΔe,j=Aq

(21)

uFF(k)=0.048θr(k)

(22)

可见前馈部分为位置主令的倍数[7]。

根据面积重心原理及误差eM和误差变化率ΔeM的归一化模糊语言值，重心点为[0.667、0.3、0.1、0、-0.1、-0.3、-0.667]。自适应控制器的输入误差范围设计为-180密位≤eM≤180密位，-80密位≤ΔeM≤80 密位，即当参考模型与系统过程的输出差值在相同时刻进入这个范围时，自适应控制器才被激活，否则不被激活。根据式(16)，以及eM和ΔeM的论域范围得出自适应控制器的输出单点Aq的取值，如表2所示。

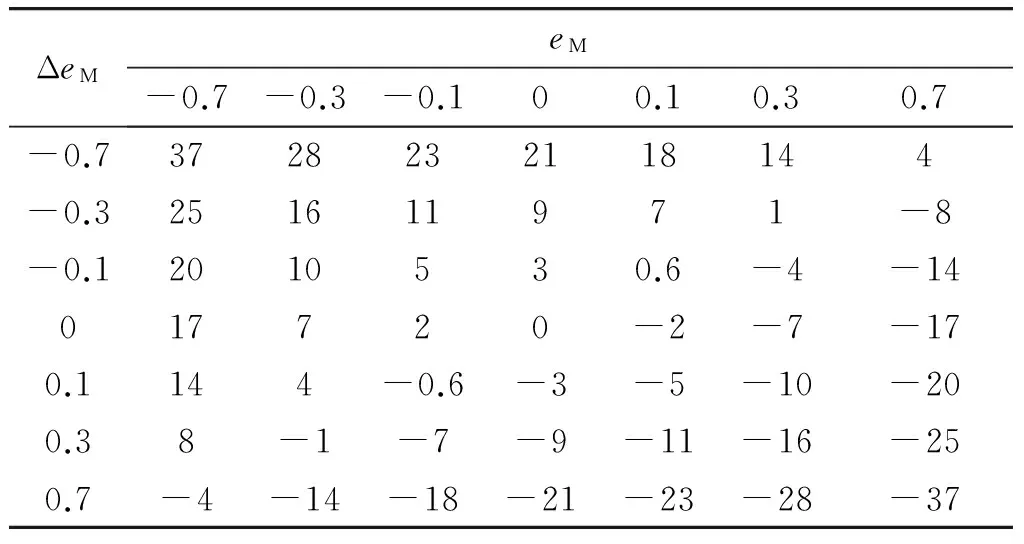
表2 自适应控制器单点输出Aq取值

2.3 自适应模糊控制器的仿真

按常规模糊控制器的仿真步骤对自适应模糊控制器进行仿真，仿真结果如图8～9所示，图8(a)中同时包含两种控制算法的动态曲线，从图中可以看出，自适应控制器系统的稳定时间大约2.8 s。为了便于观察改进效果，图8(b)将2.1 s处的图形放大，可以看到自适应将过渡过程减小了。从图9自适应输出曲线可以看到，在小于2.8 s时自适应信号开始迅速减小，相当于此时进入了之前设置的“ZO”语言值的“死区”，自适应算法不再被激活。

自适应模糊控制器正弦仿真结果如图10～11所示。

图10中系统对正弦主令进行两次自适应调整后，误差逐渐减小，从图10(b)正弦误差图看到跟踪误差范围稳定在最大3密位[8]，符合某型高炮的技术要求。

3 总结

笔者主要针对常规模糊控制器对于超调量的回调速度太慢，或者说对于小范围误差的调整速度太慢，设计了基于参考模型的自适应模糊控制器。其理论基础是通过相关文献对模糊控制器输出表达式的线性分析，得出线性控制器和模糊控制器的输出增量表达式完全一致的结论。在这个前提下，对参考模型即线性PI控制器的离散化，得出其递归方程式，与系统过程的递归方程式做差值，将两者的差值eM和ΔeM作为自适应算法的两输入，最终自适应算法输出一系列单点值作为系统的校正值，使系统的动态性能趋近与参考模型的动态性能。

References)

[1]诸静.模糊控制理论与系统原理[M]. 北京：机械工业出版社,2005:106-288. ZHU Jing. Fuzzy control theories and system principle[M].Beijing: China Machine Press，2005:106-288.(in Chinese)

[2]陈明俊，李长红，杨燕.武器伺服系统工程实践[M].北京：国防工业出版社，2013:16-56,162-190.

CHEN Mingjun,LI Changhong,YANG Yan.The weapon servo system engineering practices[M]. Beijing:National Defence Industry Press，2013:16-56,162-190. (in Chinese)

[3]陈伯时.电力拖动自动控制系统-运动控制系统[M].3版.北京：机械工业出版社, 2016:147-216. CHEN Boshi. The electric power drags along to move automatic control system-sport control system[M].3rd ed. Beijing: China Machine Press，2016:147-216. (in Chinese)

[4]赵江涛,李果,杨屹.高精度大力矩补偿机构仿真模型[J] .空间控制技术与应用,2011,37(2):26-32. ZHAO Jiangtao, LI Guo, YANG Yi. High fidelity simulation model for high torque capability compensating mechanism[J]. Space Control Technology and Application, 2011,37 (2): 26-32.(in Chinese)

[5]KOVACIC Z, BOGDAN S. Fuzzy controller design: theory and applications[J]. Macromolecular Chemistry & Physics, 2010, 205(17):23-29.

[6]ICHIKAWA B A. Application of limit fuzzy controllers to stability analysis[J]. Fuzzy Sets & Systems, 1992, 49(2):103-120.

[7]张志涌.精通MATLAB 6[M]. 5版.北京:北京航空航天大学出版社,2003:109-153. ZHANG Zhiyong. Master in MATLAB 6[M]. 5th ed. Beijing：Beihang University Press,2003:109-153. (in Chinese)

[8]黄永安.MATLAB 7.0/Simulink 6.0建模仿真开发与高级工程应用[M].北京:清华大学出版社,2005:33- 86. HUANG Yong’an. MATLAB 7.0/Simulink 6.0 models imitate true development and deluxe engineering application[M]. Beijing：Tsinghua University Press,2005:33-86. (in Chinese)

Design of Reference Model Adaptive Fuzzy Logic Control for Servo System

LEI Yu,WU Yaqiang,ZHOU Yang,SHU Lipeng

(Northwest Institute of Mechanical & Electrical Engineering，Xianyang 712099，Shaanxi，China)

The conventional fuzzy logic controller is based on heuristic control with the callback speed to the overshoot being slow. Against the background of weapon servo system and fuzzy logic control, a reference model adaptive fuzzy controller is proposed to improve its control performance. The relationship between the reference model and the recursive equation of the system process is used to determine the single point output value of the adaptive fuzzy controller. Consequently, the shortcomings of the heuristic control mode in the small error range were overcome so as to accelerate the transitional time of the system and enhance the speed tracking performance of the system. Finally, the designed controller is to meet the technical requirements of the servo system of the weapon. Simulation results verify the effectiveness of the proposed control method.

permanent magnet synchronous motor; fuzzy controller; fuzzy domain; reference model; adaptive algorithm

10.19323/j.issn.1673-6524.2017.01.012

2016-03-17

雷昱(1989—)，男，硕士研究生，主要从事火炮控制技术研究。E-mail：214355984@qq.com

TJ35

A

1673-6524(2017)01-0057-06