基于关键参数的火炮动力后坐模拟相似度评估

杨玉良，狄长春，赵建新，王 炎

(1.军械工程学院，河北 石家庄 050003；2.中国人民解放军66442部队分库，山西 阳泉 045233)

基于关键参数的火炮动力后坐模拟相似度评估

杨玉良1，狄长春1，赵建新1，王 炎2

(1.军械工程学院，河北 石家庄 050003；2.中国人民解放军66442部队分库，山西 阳泉 045233)

针对以液压为动力源的火炮后坐模拟试验方法是否与实弹射击相似的问题，提出了基于关键参数的模拟相似度评估方法。根据火炮结构原理及运动特性，选取最大后坐位移、最大后坐速度等5个关键参数为相似元，采用对比最值的方式计算各关键参数的相似度值，采用区间层次分析法计算各关键参数的权重系数，最后开展模拟相似度评估。评估结果验证了该试验方法的有效性，为动力后坐模拟试验装置的进一步应用提供了可靠依据。

火炮；动力后坐；实弹射击；关键参数；模拟相似度评估；区间层次分析法

近年来，以液压为动力源的火炮动力后坐模拟试验方法成为研究热点[1]。该试验方法的工作原理如图1所示。通过液压系统将冲击头加速到一定速度，然后高速冲击头与液压系统脱离，撞击炮口以推动火炮后坐，进而完成火炮后坐及复进过程的模拟。冲击头前侧的波形发生器在冲击过程中起着调节冲击载荷波形的作用。动力后坐模拟试验时，推动火炮后坐的主动力为作用于炮口的冲击力。

针对动力后坐与实弹射击是否相似、相似度如何评估的问题，笔者提出基于关键参数的模拟相似度评估方法，并根据两种条件下的关键参数取值情况开展模拟相似度评估。

1 模拟相似度评估理论

模拟相似度是指模拟系统与真实系统在某些特性(相似元)的相似程度。本文中，真实系统对应实弹射击试验，模拟系统对应动力后坐试验。

设模拟系统为A，真实系统为B，系统A与B之间构成n个相似元，每个相似元的值为qi，每个相似元对系统相似度的影响权重为βi，则系统A与B的相似度可以定义为

(1)

由式(1)可知，模拟相似度数值是由相似元数量、相似元值以及每个相似元对系统相似度影响的权重系数等因素决定的。

2 相似元的选取

根据评估理论计算动力后坐模拟相似度时，应首先选取能够表征火炮在两种试验条件下动态特性的相似元。

反后坐装置是火力系统的重要组成部分，被誉为火炮的“心脏”，主要由复进机和驻退机组成。反后坐装置不仅影响火炮受力和运动规律，还影响着火炮射速和精度，因此模拟相似度评估时应重点分析反后坐装置。参照国军标《火炮动态后坐模拟试验方法》相关规定，结合反后坐装置的重要作用，选取最大后坐位移、最大后坐速度以及最大后坐速度对应的时间和位移、最大后坐阻力这5个关键参数，对动力后坐与实弹射击条件下后坐动态特性进行对比分析。

基于关键参数开展模拟相似度评估时，相似元为5个关键参数，相似元值为每个关键参数的相似度值，权重系数为每个关键参数相似度在模拟相似度中所占的比重。在以上论述基础上，提出动力后坐模拟相似度的评估方法如图2所示。

3 关键参数相似度值的计算

分别开展动力后坐模拟试验和实弹射击试验，采用位移传感器、压力传感器等测试以上5个关键参数。

采用对比最值的方式，分别计算5个关键参数的相似度值，计算公式为

(2)

关键参数相似度值的计算结果如表1所示。

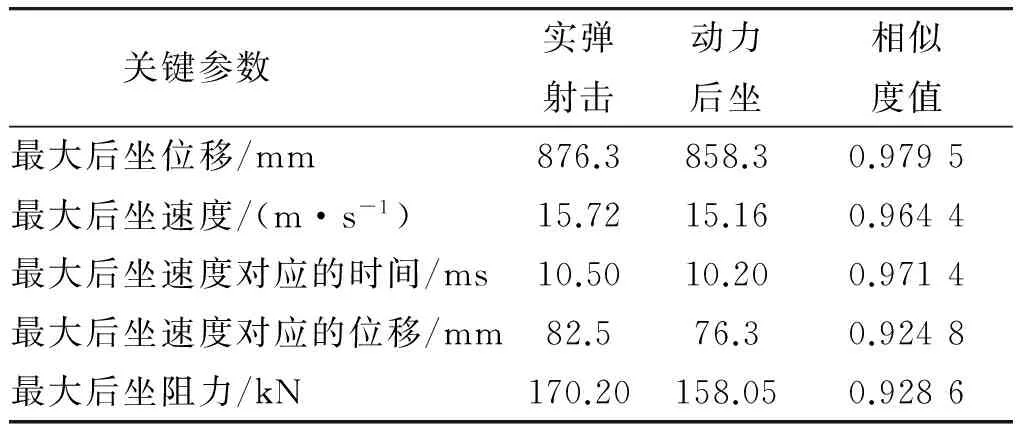
表1 关键参数的相似度值

4 关键参数权重系数的计算

层次分析法由美国学者Satty等提出，是一种定性和定量相结合、层次化的多准则决策方法。采用层次分析法时，评判专家根据经验及知识积累，对评价指标的相对重要程度进行两两比较，给出判断值，进而建立判断矩阵，然后根据判断矩阵计算出评价指标的权重系数。但是，在评价指标相对重要程度两两比较过程中，评判专家有时难以给出一个确定判断值进行描述，或者不同专家的判断值存在一定范围的差异。针对这些不确定判断，采用传统层次分析法的点值描述是不太合理的。

4.1 区间层次分析法

区间层次分析法将传统层次分析法与区间数学融合一起，采用区间数代替点值，进而构造区间数判断矩阵，然后根据区间数判断矩阵计算出评价指标的权重系数[2]。采用区间层次分析法计算权重系数，主要分为构造区间数判断矩阵、计算区间权重向量和计算单一权重向量3个过程。

4.1.1 构造区间数判断矩阵

(3)

判断矩阵取值多采用1～9标度法和指数标度法。1～9标度法缺陷很多，一是排序权值较粗，二是有可能出现与实际相反的排序，三是矩阵一致性与思维一致性脱节，而指数标度法很好地解决了以上缺陷[3]。指数标度法的具体含义如表2所示。

表2 指数标度法

判断矩阵A=(aij)n×n中的元素满足

(4)

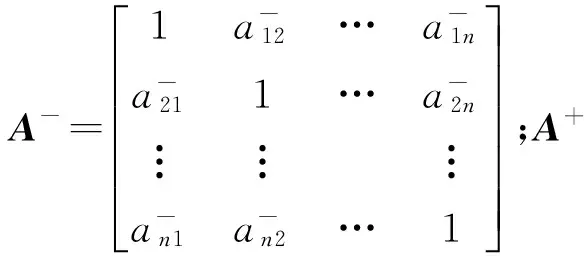
4.1.2 计算区间权重向量

求解区间数判断矩阵时，区间数特征根法计算过程较为简单，精度较高，且该方法具有严密的数学基础，因此采用区间数特征根法求解区间数判断矩阵[4-5]。计算步骤如下[6-7]：

1)分别计算下限矩阵A-和上限矩阵A+的最大特征值λ-、λ+，得出特征值对应的具有正分量的归一化特征向量x-、x+。

2)根据A-、A+计算出特征向量的对应系数k1和k2。

(5)

3)计算区间权重向量

W=[W-,W+]=[k1x-,k2x+]

(6)

4)检验区间数判断矩阵的一致性检验标准为

(7)

式中：δ(A)为A的平均模糊程度，表达式为

(8)

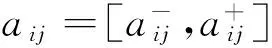
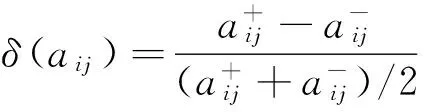
(9)

λ*为λ=[λ-,λ+]的代表值，表达式为

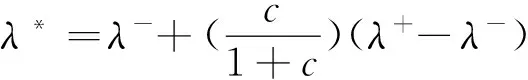
(10)

c为矩阵正负偏差的比值，表达式为

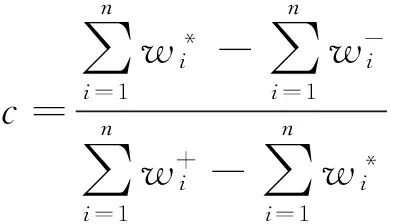
(11)

表3 不同阶判断矩阵RI取值

4.1.3 计算单一权重向量

由于计算出的权重向量仍为区间数，而在实际应用时权重应为单一特定值，根据文献[8]，设定区间数服从均匀分布。

计算单一权重向量步骤为：

1)将区间权重向量下、上限值进行均值化处理

(12)

2)将单一权重向量进行归一化处理

(13)

4.2 权重系数的计算

采用区间层次分析法对5个关键参数的权重系数进行计算。

4.2.1 构造区间数判断矩阵

根据各关键参数对模拟相似度的影响重要性进行两两对比，并采用指数标度法表征，得到区间数判断矩阵，如表4所示，表中V1、V2、V3、V4、V5分别表示最大后坐位移、最大后坐速度、最大后坐速度对应的时间、最大后坐速度对应的位移、最大后坐阻力。

表4 区间数判断矩阵

将a=1.316代入表4中，可得下限矩阵为

上限矩阵为

4.2.2 计算区间权重向量

分别计算下限矩阵A-和上限矩阵A+的最大特征值λ-=4.404 8、λ+=5.735 2，对应特征向量分别为

x-=[0.286 0,0.242 4,0.140 7,0.125 5,0.205 5]T

x+=[0.305 4,0.231 4,0.140 9,0.126 6,0.195 7]T。

特征向量对应系数k1=0.935 6、k2=1.064 0。因此得出区间权重向量W=([0.267 6,0.324 9],[0.226 8,0.246 2],[0.131 6,0.149 9],[0.117 4,0.134 7],[0.192 3,0.208 2]) 。

对区间数判断矩阵进行一致性检验，c=1.006 3，λ*=5.072 1，δ(A)=0.325 5 。根据以上数据计算出CR=0.025 0≤0.1×(1+δ(A))=0.132 6，验证了区间数判断矩阵的一致性。

4.2.3 计算单一权重向量

设定区间数为均匀分布，将区间权重向量进行均值化、归一化处理，得出5个关键参数的权重系数，如表5所示。

表5 关键参数的权重系数

4.3 模拟相似度评估

基于模拟相似度评估理论，根据表1和表5数据，采用式(1)计算出基于关键参数的动力后坐模拟相似度为0.957 7。

5 结束语

针对动力后坐与实弹射击是否相似、如何评估的问题，提出了基于关键参数的模拟相似度评估方法。分别采用对比最值法、区间层次分析法得出了关键参数的相似度值和权重系数，最后评估出模拟相似度为0.957 7，评估结果验证了动力后坐模拟试验方法的合理性，为其应用于实际试验、部分代替实弹射击提供了可行性论证。

References)

[1]刘林, 狄长春, 潘保青, 等. 火炮动力后坐仿真模拟试验装置设计研究[J]. 火炮发射与控制学报, 2011(3): 36-40. LIU Lin, DI Changchun, PAN Baoqing, et al. Design and research on gun dynamic recoil simulation test mechanism[J]. Journal of Gun Launch & Control, 2011(3): 36-40. (in Chinese)

[2]周毅, 赵晓刚. 基于区间层次分析法的石油库防火防爆安全评价[J]. 中国安全科学学报, 2011, 21(12): 58-63. ZHOU Yi, ZHAO Xiaogang. Safety assessment for fire and explosion of petroleum depot based on IAHP[J]. China Safety Science Journal, 2011, 21(12): 58-63. (in Chinese)

[3]吕跃进, 张维. 指数标度在AHP标度系统中的重要作用[J]. 系统工程学报, 2003, 18(5): 51-60. LYU Yuejin, ZHANG Wei. Kernel function of index scale in AHP scale system[J]. Journal of Systems Engineering, 2003, 18(5): 51-60. (in Chinese)

[4]KWONG K C，BAI H．A fuzzy AHP approach to the determination of importance weights of customer requirements in quality function deployment[J]．Journal of Intelligent Manufacturing, 2012, 13(5): 367-377.

[5]李姗姗. 基于IAHP的生产系统作业疲劳模糊综合评价[J]. 武汉理工大学学报：信息与管理工程版，2014, 36(3): 30-33. LI Shanshan. Fuzzy comprehensive evaluation for operation fatigue in production system based on IAHP[J]. Journal of Wuhan University of Technology：Information & Management Engineering, 2014, 36(3): 30-33. (in Chinese)

[6]汤天培, 徐勋倩, 赵胜男. 综合客运枢纽静态导向标识系统评价研究[J]. 广西大学学报：自然科学版, 2013, 38(6): 1389-1395. TANG Tianpei, XU Xunqian, ZHAO Shengnan. Study on evaluation of static guiding sign system of comprehensive passenger terminal[J]. Journal of Guangxi University：Natural Science Edition, 2013, 38(6): 1389-1395. (in Chinese)

[7]翟晓燕, 张新政. 群决策中区间数判断矩阵的集结及权重的计算[J]. 系统工程, 2005, 23(9): 103-107. ZHAI Xiaoyan, ZHANG Xinzheng. The methods on aggregation of interval number judgment matrixes and calculation of its priorities in the group decision-making[J]. Systems Engineering, 2005, 23(9): 103-107. (in Chinese)

[8]李曙林, 陈宁, 杨哲, 等. 基于区间数的飞机生存力评估方法[J]. 空军工程大学学报：自然科学版, 2004, 15(1): 1-4. LI Shulin, CHEN Ning, YANG Zhe, et al. Evaluation method of aircraft survivability based on interval number[J]. Journal of Air Force Engineering University：Natural Science Edition, 2004, 15(1): 1-4. (in Chinese)

Simulation Similarity Evaluation of Gun Dynamic Recoil Based on Key Parameters

YANG Yuliang1, DI Changchun1, ZHAO Jianxin1, WANG Yan2

(1.Ordnance Engineering College, Shijiazhuang 050003, Hebei, China;2.Storage of PLA Unit 66442 , Yangquan 045233, Shanxi, China)

Aiming at the similarity problem between the gun dynamic recoil simulation test method with hydraulic source and the live firing, advanced was the simulation similarity evaluation method based on key parameters. According to the structure principle and motion characteristic, five parameters were selected as similarity elements, comprising the maximum recoil displacement, the maximum recoil velocity and so on. The most value contrast method was used to calculate similarity values of key parameters. The interval analytic hierarchy process method was used to calculate weight coefficients of key parameters. Finally, the simulation similarity was evaluated. The evaluation result indicated the validity of the test method, which provided a reliable basis for the further application of dynamic recoil simulation test equipment.

gun; dynamic recoil; live firing; key parameters; simulation similarity evaluation；interval analytic hierarchy process method

10.19323/j.issn.1673-6524.2017.01.015

2016-03-17

杨玉良(1987—)，男，博士，主要从事武器系统动力学仿真技术研究。E-mail：yyl_liang@sina.com

TJ301

A

1673-6524(2017)01-0074-05