弹药参数及误差对弹头膛内运动的影响研究
2017-03-28刘国庆
刘国庆,徐 诚
(南京理工大学 机械工程学院,江苏 南京 210094)
弹药参数及误差对弹头膛内运动的影响研究
刘国庆,徐 诚
(南京理工大学 机械工程学院,江苏 南京 210094)
为深入了解狙击步枪枪弹参数、误差对弹头膛内运动过程的影响,基于非线性有限元法建立了某型狙击步枪弹/枪相互作用数值计算模型,并通过试验验证了模型的正确性。重点考虑了弹头结构参数与材质、弹/药参数误差对弹头膛内运动的影响,定性、定量地分析了参数及误差对弹头膛内摆动角、轴向受力、膛压及初速的影响规律,揭示了狙击弹参数及误差与弹头膛内运动间的关系,有利于提高对狙击弹设计工作的认知水平。
有限元;狙击步枪;弹丸参数;内弹道;摆动角
狙击弹通常由弹头、火药、底火与弹壳4部分组成而完成发射过程,各组成部分对全弹道过程各阶段的影响程度不同,因而其设计内容及侧重点有明显差异,有设计参数与控制参数之分。
在全弹道过程中,枪弹参数与各个弹道阶段均密切相关,学者们从多个角度开展了相关研究。目前研究成果多集中在终点弹道,侧重研究弹头速度、入射角度与材质对多种防护条件下的靶标侵彻[1-3];在外弹道方面,主要关注弹头结构、弹形系数对射击精度的影响及其水下运动弹道的动力学分析[4-5];在内弹道方面则主要对挤进过程、弹带宽度、弹炮间隙与导引部长度等方面进行了研究[6-10]。
弹头膛内运动过程对弹丸参数、误差的敏感性
最大,揭示弹丸参数及误差对弹头膛内运动的影响规律将提高弹丸设计工作的认知水平,但是目前狙击步枪弹丸参数对射击精度影响的理论或试验研究成果较少,现有的理论计算模型及结果往往是不完善、不精确的,缺乏研究平台及研究成果。因此笔者针对某型狙击步枪建立了弹/枪相互作用数值计算模型,考虑内弹道过程中多种初始条件,从弹头结构参数与材质、弹药参数误差两方面着重分析参数变化及其误差对弹头膛内运动的影响情况。
1 弹/枪相互作用有限元模型及其验证
1.1 计算模型
依据枪管、狙击弹结构参数分别建立三维模型,使用有限元前处理软件进行网格划分,其网格模型如图1、2所示。网格类型以六面体缩减积分实体单元为主,其中枪管共划分267 529个网格,弹头壳共划分175 769个网格,铅芯共划分110 868个网格。
装配时,弹头处于坡膛前部,与实际装配位置一致,由有限元程序计算挤进过程及后续内弹道过程。模型考虑了重力作用导致的枪管预弯曲现象,通过显隐式混合运算实现;此外,还考虑了弹头膛内运动与膛压之间的耦合作用,通过有限元软件的用户子程序功能实现内弹道计算与有限元计算的耦合[11]。
1.2 模型的验证
采用铜柱测压法进行了膛压测试试验,采用光电法进行了初速测试试验,试验与仿真结果对比如表1所示,其中v0、Pm分别为初速、膛压。对比数据可知计算结果与试验结果一致性较高,膛压与初速误差小于1%,从而证明了计算模型的正确性、有效性。

表1 数据对比表
2 参数影响分析
以弹/枪相互作用有限元计算模型为平台,分别考虑弹头结构参数、材质对内弹道过程中弹头摆动、轴向受力、膛压与初速等方面的影响情况。
2.1 圆柱部结构参数
2.1.1 对弹头摆动、初速的影响
弹头圆柱部结构参数可分为圆柱部直径Φ和长度l,在这2个参数设计范围内均匀地选取5个参数值,如表2所示,表中所示为参数值与标准设计参数的相对值,参数变化对弹头膛内摆动角θ的影响如图3所示。
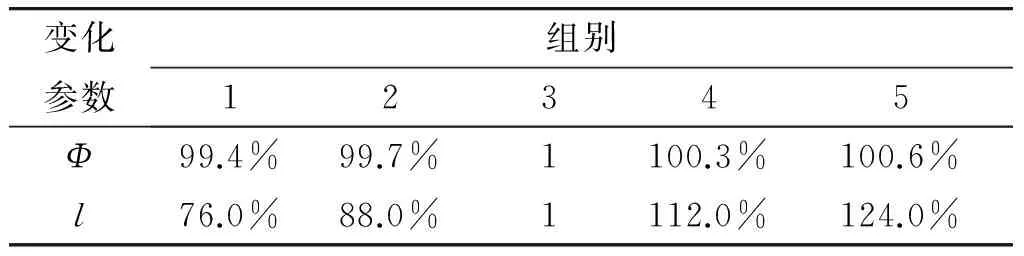
表2 圆柱部结构参数
从图3可以看出,随圆柱部直径的增大,弹头摆动角总体上呈现先增后减的趋势,在(99.4%~1)Φ范围内的摆动角相对稳定,摆动角差值约为0.12 mrad;圆柱部长度增加则弹头摆动角呈现先减后增的趋势,摆动角差值约为0.57 mrad;圆柱部的长度等效于克服摆动运动的阻力力矩,阻力力矩越长则起到的缓冲与降低摆动的能力越好,但阻力力矩过长将减弱这种作用。
弹头圆柱部参数对弹头初速的影响如表3所示,圆柱部直径、长度对初速的影响基本相同,随着圆柱部直径的增大、圆柱部长度的增加,弹丸初速逐步增大。弹头初速最大差值约为32 m/s,相对于理论初速值偏差为3.54%。
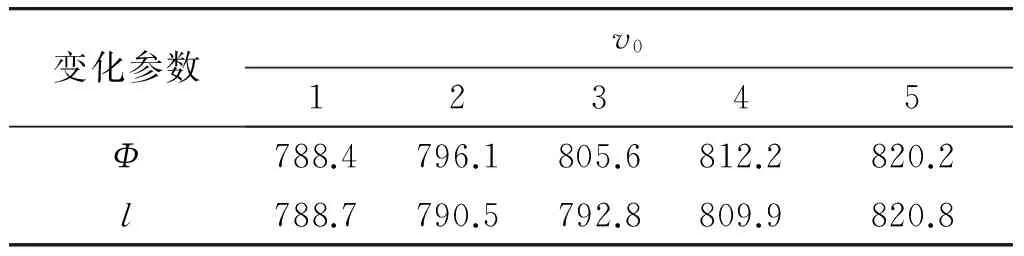
表3 对弹头初速的影响 m/s
2.1.2 对弹头轴向受力的影响
弹头圆柱部参数对弹头轴向受力的影响如图4、5所示,弹头轴向受力随着圆柱部直径的增大、长度的增大而增加。0.6 ms之前(挤进过程),圆柱部参数对轴向受力的影响较大,因参数变化导致的轴向受力差值约为500 N,0.6—0.9 ms之间,轴向受力差值逐步缩小,此时间段内弹头塑性变形逐渐完成,0.9 ms之后,圆柱部参数变化对弹头轴向受力的影响基本消失,轴向受力差值仅为50 N,表明圆柱部参数对挤进过程中的轴向受力影响较为明显,但随着弹头塑性变形的逐渐完成,轴向受力差值逐步降低。
2.2 弹头材料
狙击弹弹头由软质的铜弹头壳与铅弹芯组成,弹头材料的刚度直接与弹/枪相互作用有关,笔者从理论上分析弹头材料变化对内弹道过程的影响情况。
2.2.1 弹头壳对内弹道过程的影响
假设屈服应力改变后,塑性阶段的应力-应变关系发生同等变化,其他材料属性不变。屈服应力改变对弹头膛内摆动角的影响如表4所示。

表4 屈服应力变化对弹头摆动角的影响
表4所示,在0.6σs~σs范围内弹头摆动角逐步降低,摆动角降低了1.02 mrad,在σs~1.4σs范围内弹头摆动角逐步增大,摆动角增大了0.23 mrad。弹头壳具有吸收弹头运动过程中摆动能量的作用,缓冲弹/枪间的相互作用,而弹头壳的屈服应力与缓冲作用的能力有关,当弹头壳屈服应力太小或太大,都将使这种缓冲作用效果较弱,从而导致摆动程度加剧。
弹头壳屈服应力变化对弹头轴向受力的影响如图6所示,屈服应力变化主要影响挤进过程中的轴向受力,此阶段的轴向受力大小随弹头壳材料“变硬”而增大,图中A1处轴向受力最大相差约312.5 N,A2处轴向受力最大相差450 N,A3处轴向受力最大相差333.6 N,挤进过程中轴向受力上升速率与弹头壳屈服应力值呈正比关系;挤进完成后,弹头壳弹塑性变形逐渐充分,轴向受力差值逐渐减低,差值最终稳定在150 N左右。
2.2.2 弹芯对内弹道过程的影响
假设弹芯材料除应力-应变关系外,其他材料属性均保持不变,弹芯为铅、铜、钢3种材料条件下的弹头膛内摆动角、轴向受力情况如表5、图7所示。

表5 弹芯材料种类对弹头摆动角的影响
弹芯材料种类改变并未对弹头膛内摆动角产生明显影响,摆动角差值仅为0.1 mrad,但弹头所受轴向力却有非常显著的变化,弹芯材料为钢、铜时,弹头轴向受力最大峰值分别达到了7 468.4、5 190.9 N,弹芯材料变化直接导致了弹头轴向力的显著增大;弹芯材料变化对挤进完成后的影响逐渐降低,如挤进过程中的最大轴向力A处的差值分别为2 277.5、3 088.4 N,而B处的差值分别为127.2、1 169.1 N。上述现象表明弹芯强度变化对内弹道过程的影响主要体现在弹头受力方面,而对弹头膛内摆动角的影响非常小,其中对挤进阶段轴向力的影响大于挤进完成后的后续内弹道阶段。内弹道过程中,弹头壳与枪管、弹芯之间存在挤压作用,当弹芯为软质材料时,挤压作用弱则径向力、轴向力较小;当弹芯为硬质材料时,挤压作用强则径向力、轴向力较大。
弹芯材质的改变导致弹头轴向受力产生如此明显的变化,必将对内弹道其他特征量产生影响,图8、表6所示为弹芯材质对内弹道阶段膛压与速度的影响。

材料种类铅铜钢v0/(m·s-1)792.8828.2902.5
图8所示,3种弹芯状态下的膛压变化规律,弹头所受轴向力越大则最大膛压值越大,弹芯材料为钢、铜时,最大膛压值为494.4、390.2 MPa,二者远远高于标准膛压值(299.5 MPa),但在内弹道过程后期,三者的膛压差慢慢缩小,膛压最大差值约为33.5 MPa。表6所示,钢芯弹头速度最大,其次为铜芯、铅芯,速度变化规律与膛压变化规律类似。这种现象符合火药燃烧的基本规律,即弹头轴向受力越大则最大膛压值、初速越高。
3 参数误差影响分析
枪弹误差主要包括弹头质量偏心、弹重误差与火药装填误差,笔者将分析枪弹参数误差对弹头膛内运动、轴向受力、膛压与初速的影响。
3.1 质量偏心
3.1.1 对弹头摆动角的影响
弹头质量偏心是不可避免的现象,高速自转的弹头将产生不可忽视的离心惯性力,从而必然加剧弹头膛内摆动,表7所示为不同质量偏心距e时弹头膛内摆动情况。有质量偏心时的弹头摆动角远高于无质量偏心状态,且高于其他因素带来的影响;有偏心状态下的摆动角相对于无质量偏心状态分别增大了5.4、7.6、11.1和16.5倍。

表7 不同质量偏心距对弹头膛内摆动的影响
3.1.2 偏心方位对弹头膛内运动的影响
实际质心位于质心面内以偏心距为半径的圆周之上,其方位是随机的。假设实际质心位于4个象限点处,偏心距为0.05 mm,弹头头部在4种方位条件下的位移轨迹如图9所示,弹轴向运动由右手定则确定。
图9所示,当实际质心方位对称时,弹头头部位移具有对称趋势,但位移的幅值基本不变,幅值增长至一定程度后基本保持不变,表明偏心距一定的情况下位移幅值有极限值。位移曲线到达波峰、波谷的相位差与偏心方位差一致,因此可以判断任意方位情况下弹头头部位移曲线全部位于由4个象限点所形成的位移曲线区域内。
3.2 弹重误差
弹头质量m是内弹道方程的重要初始量,误差的存在势必影响膛压的生成规律与弹头初速。
3.2.1 对最大膛压、初速的影响
表8所示为弹重误差对最大膛压、初速的影响,其中Δ表示弹重最大误差控制值。弹重增大则最大膛压值与初速值均增大,弹头膛内停留时间变短,弹重每变化一个Δ则最大膛压值变化约15 MPa,初速值变化约15.6 m/s,弹头膛内时间变化约0.02 ms。

表8 弹重误差对最大膛压、初速的影响
3.2.2 对弹头膛内摆动的影响
表9所示弹重误差对弹头膛内摆动的影响较小,摆动角最大差值仅为0.15 mrad,表明弹头摆动角对弹重误差的变化并不敏感。

表9 弹重误差对弹头膛内摆动的影响
3.3 火药装填参数误差
火药装填参数误差通过影响膛压而与弹头运动产生耦合作用,选取装药量ω、火药力f与药室容积W0这3个参数研究火药装填参数误差对最大膛压、初速与弹头膛内摆动的影响,Δ与弹重误差的意义相同。
3.3.1 对最大膛压、初速的影响
装药量、火药力与药室容积在误差范围内对最大膛压的影响如表10所示,对初速的影响如表11所示。
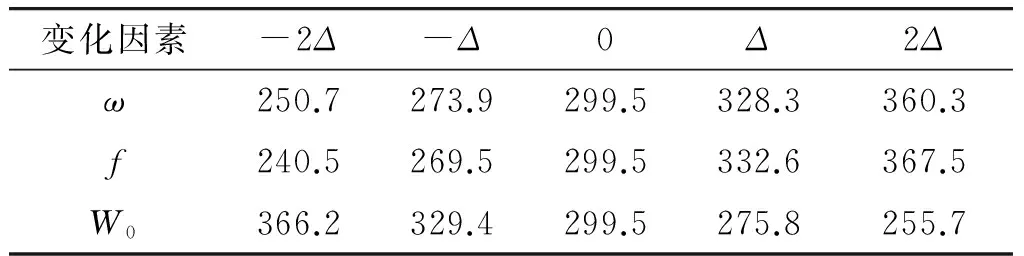
表10 对最大膛压的影响 MPa

表11 对初速的影响 m·s-1
装药量、火药力与最大膛压、初速基本呈现正比关系,相对于标准状态,装药量每变化Δ则膛压平均变化27.51 MPa,初速平均变化55.86 m/s;火药力每变化Δ则膛压平均变化34.1 MPa,初速平均变化63.14 m/s。药室容积与最大膛压、初速近似成反比关系,药室容积每变化Δ则膛压平均变化28.35 MPa,初速平均变化60.26 m/s。
3.3.2 对弹头摆动的影响
图10所示为火药参数误差对弹头摆动角的影响情况。结合表10、11与图10数据可知,当上述火药参数误差导致膛压增加(降低)时,弹头的摆动程度较为剧烈(平缓);最大膛压值稳定在275~300 MPa内时,弹头的摆动程度最为平缓,此膛压区间对应的初速区间为750~790 m/s。
4 结论
基于弹/枪相互作用数值计算模型,分析了弹丸主要结构参数、参数误差对内弹道过程中弹头摆动、轴向受力、膛压与初速等方面的影响情况,得到如下几点结论:
1)在所需参数值范围内,圆柱部直径取小值、长度取大值有利于降低弹头膛内摆动角,二者参数值增大均能小幅度增加初速与轴向受力,参数值变化对轴向阻力的影响在弹头塑性变形完成之后基本消失。
2)弹头壳屈服应力在0.6σs~1.4σs范围内时,铜质弹头壳缓冲弹头摆动的能力最好;弹头塑性变形完成前,轴向受力最大值及增长速率随弹头壳强度的增加而增大;弹芯强度变化对弹头摆动影响较小,弹芯强度增加则轴向受力、膛压与初速明显增大。
3)弹头摆动程度随偏心距的增大而剧烈,质量偏心对弹头摆动的影响远远高于其他因素;弹头头部摆动位移幅值只与偏心距有关,且位移幅值有极限值,任意偏心方位情况下的弹头头部位移曲线位于由4个象限点所形成的位移曲线区域内。
4)弹重误差与最大膛压、初速与内弹道持续时间具有比例关系,而对弹头膛内摆动基本没有影响。
5)火药装填参数误差与最大膛压、初速之间具有较为稳定的比例关系,当参数误差使得最大膛压稳定在275~300 MPa区间时,弹头的摆动程度最平缓,此膛压区间对应的初速区间为750~790 m/s。
References)
[1]温垚珂, 徐诚. 步枪弹侵彻明胶靶标的数值模拟[J]. 兵工学报, 2013, 34(1):14-19. WEN Yaoke, XU Cheng. Numerical simulation of the penetration of bullet on gelatin target[J]. Acta Armamentarii,2013, 34(1):14-19.(in Chinese)
[2]杨正有. 弹丸对运动靶的侵立与贯穿效应研究[D]. 北京:北京理工大学,2015. YANG Zhengyou. The research on projectile partial penetration and perforation into moving target[D]. Beijing: Beijing Institute of Technology, 2015. (in Chinese)
[3]何雨.长杆弹撞击下金属靶板侵彻与穿透的进一步研究[D]. 合肥:中国科学技术大学,2013. HE Yu. Further study on the penetration and perforation of metallic targets struck by long rods[D]. Hefei:University of Science and Technology of China, 2013. (in Chinese)
[4]侯宏录, 王赛, 闫帅. 弹道参数对弹丸落点的影响分析[J]. 西安工业大学学报, 2009, 29(3):209-213. HOU Honglu, WANG Sai, YAN Shuai. Impact analysis of ballistic parameters on placement of bullet[J]. Journal of Xi’an Technological University,2009, 29(3):209-213. (in Chinese)
[5]宋浩伟. 弹丸水下高速运动外弹道建模与仿真[D]. 南京:南京理工大学,2007. SONG Haowei. The modeling and simulation of external ballistic bullet with high velocity under water[D]. Nanjing: Nanjing University of Science and Technology,2007. (in Chinese)
[6]刘国庆, 徐诚. 狙击步枪弹准静态弹头挤进力研究[J]. 兵工学报, 2014, 35(10):1528-1535. LIU Guoqing,XU Cheng. Research on quasi-static engra-ving force of sniper rifle bullet[J]. Acta Armamentarii, 2014, 35(10):1528-1535. (in Chinese)
[7]黄彦.弹丸挤进模拟试验系统载荷特性研究[D]. 南京:南京理工大学,2009. HUANG Yan. Load characteristics research of testing system of bullet engraving simulation[D]. Nanjing:Nanjing University of Science and Technology,2009. (in Chinese)
[8]黄文祥.弹丸挤进变形模拟问题研究[D]. 南京:南京理工大学,2009. HUANG Wenxiang. The research of bullet deformation in engraving simulation praocess[D]. Nanjing:Nanjing University of Science and Technology,2009. (in Chinese)
[9]孙河洋,马吉盛,李伟.坡膛结构变化对弹带挤进过程影响的研究[J].振动与冲击, 2011,30(3):30-33. SUN Heyang, MA Jisheng, LI Wei. Influence of different bore structures on engraving process on projectile[J]. Journal of Vibration and Shock,2011,30(3):30-33. (in Chinese)
[10]岳永丰,吴群彪,沈培辉.弹丸结构参数对膛内运动的影响分析[J].兵工自动化, 2013,32(3):35-38. YUE Yongfeng, WU Qunbiao, SHEN Peihui. Influence analysis of projectile structural parameters on motion in bore[J]. Ordance Industry Automation, 2013,32(3):35-38. (in Chinese)
[11]丁传俊,张相炎. 基于热力耦合有限元模型的弹带挤进过程及内弹道过程的仿真研究[J]. 兵工学报,2015,36(12):2254-2261. DING Chuanjun, ZHANG Xiangyan.Simulation study of bearing band engraving process and interior ballistic process based on thermo-mechanical coupling FEA model[J]. Acta Armamentarii, 2015,36(12):2254-2261. (in Chinese)
The Influence of Parameter and Error of Bullet-powder on Movement in Internal Ballistic Process
LIU Guoqing, XU Cheng
(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094,Jiangsu,China)
The numerical model of interaction between bullet and sniper rifle was established to deeply study the influence of bullet parameter on internal ballistic process, which is based on nonlinear finite element theory. The accuracy of this model was proved in experiments. The following factors are taken into account as influence of structural parameter and material of bullet, parameter error of bullet-powder on movement in internal ballistic. Qualitative and quantitative analysis is conducted of the influen-ce rule of parameter and error on swing angle, axial force, bore pressure and initial velocity. A revelation is found out of the relationship of parameter and error of bullet-powder to movement in internal ballistic process. It is beneficial for the improvement of the cognition level in the design of sniper rifle bullets.
finite element; sniper rifle; parameter of bullet; internal ballistic; swing angle
10.19323/j.issn.1673-6524.2017.01.001
2016-03-16
国家自然科学基金项目(51575279)
刘国庆(1988—),男,博士,主要从事武器系统仿真分析技术研究。E-mail:guoqingcool@126.com
TJ22
A
1673-6524(2017)01-0001-06
