基于三参数威布尔分布的自动调整臂服役可靠性研究

罗 哉,王 艳,王岚晶,刘 晖

(中国计量大学，杭州 310018)

基于三参数威布尔分布的自动调整臂服役可靠性研究

罗 哉,王 艳,王岚晶,刘 晖

(中国计量大学，杭州 310018)

作为汽车制动系统关键部件的自动调整臂,其服役可靠性关系到汽车行驶的安全;通过疲劳试验分析自动调整臂零部件失效的可能性，试验结果表明：矩形压簧及螺旋压缩弹簧是影响自动调整臂失效的关键部分;利用MATLAB分析试验数据，可知自动调整臂疲劳寿命服从三参数的威布尔分布，文中结合竞争性故障模型对自动调整臂的服役可靠性进行分析，基于该模型采用最小二乘法及最大相关系数法对试验中的寿命数据进行参数估计；实例分析表明,该法的原理简单，方便实用，结合竞争性故障模型的威布尔分布能准确真实地反映自动调整臂疲劳试验数据的统计特性，具有较好的工程应用价值。

自动调整臂；威布尔分布；竞争性故障模型；最小二乘法

0 引言

自动调整臂长期工作在频繁制动、高载荷和复杂工况等环境下，其本身的失效是难以避免的，这也是汽车制动性能长期稳定的严重威胁[1]。因此，对自动调整臂的服役可靠性进行研究，将有利于产品检验员提前杜绝制动系统发生失效的可能性，对提高车辆行车制动的安全性和可靠性具有重要的意义。自动调整臂的结构爆炸图和实物图如图1和图2。

图1 自动调整臂结构爆炸图

图2 自动调整臂实物图

机械产品可靠性分析主要是运用各种统计分布，现有研究中通常采用正态分布或对数正态分布来描述疲劳寿命,但在许多情况下，威布尔分布已被证明是能够更好地描述疲劳寿命的分布。正态分布一般适用于中等寿命区，疲劳寿命大致在104～106循环，威布尔分布并不局限于这个范围。对于疲劳寿命大于104循环的长寿命区,有些试验结果也近似符合威布尔分布[2]。正态分布在零件失效概率很小时，其疲劳寿命趋近于零，这与实际情况不符。而三参数威布尔分布有个位置参数，可以弥补正态分布理论在疲劳寿命试验中的不足[3-4]。只要是因为某一局部疲劳失效或者故障而引发系统失效的元器件或系统的强度和疲劳寿命均服从威布尔分布[5]。

以往对机械产品进行可靠性分析都是直接分析其发生故障或者失效时寿命，并没有具体考虑是由机械产品的哪个零部件产生的。自动调整臂的失效通常是由于某个零部件发生故障损坏产生的，又因为自动调整臂的各个零部件具有独立性[6]，即任何一个零部件失效都会使自动调整臂失效，因此必须找到最容易失效的零部件对其进行分析。通过疲劳实验得知，螺旋压缩弹簧和矩形压簧是自动调整臂失效的主要因素，因此本文结合竞争性故障模型以及威布尔分布对自动调整臂的可靠性进行预测。

1 威布尔分布模型

威布尔分布是近年来在设备寿命可靠性分析中使用最广泛的模型之一[7-9]。在自动调整臂的疲劳实验中，通过自动调整臂实验的次数来记录其是否失效。因此将威布尔分布函数中的产品正常工作时间t转化为产品应力循环次数N[10]，则威布尔分布的概率密度函数为:

(1)

式中，m为形状参数；Na为尺度参数，或称特征参数；No为位置参数，或称最小寿命参数。

其中，失效次数n≤N的概率，即不可靠度函数为：

(2)

将式(2)代入式(3),并进行积分,得累积失效概率函数和失效率函数分别为:

(3)

(4)

由于螺旋压缩弹簧与矩形压簧是导致自动调整臂失效的两个独立因素，因此在数据处理上不能采用典型的单一分布进行拟合或分析，需要采用竞争性故障模型进行分析。

2 竞争性故障模型

如果系统有K种失效方式，而每一种失效方式都独立作用于系统，且都对应一定的失效时间，其中任何一种失效都会引起系统的失效即称为竞争失效[11]。在所有的失效中所对应的失效产生最早的那种失效出现时，将导致系统失效，即:

T=min{T1,T2,…,TK}

下面则是竞争性模型累积失效分布函数的通用表达式，当K个因素同时起作用时，系统的可靠度为:

式中,λi(t)是对应第i个失效因素的失效率。系统的总失效率将是对应时刻t的K个独立失效率的和，即:

λ(t)=λ1(t)+λ2(t)+…+λK(t)

显然，对于K个常数失效率，系统为指数分布。自动调整臂的疲劳失效分布为威布尔分布，由上面的公式(4)可知，其失效率函数和可靠度函数分别为:

(5)

(6)

其中:N为自动调整臂失效时的实验次数，形状参数mi、尺度参数Nai和位置参数N0需要通过参数估计来拟合。

3 三参数威布尔分布的参数估计

威布尔分布参数估计的常用方法是极大似然方法和最小二乘法，可适用于完全样本和截尾样本[12]。威布尔分布极大似然方法需要在实数范围内，搜索求解极大似然超程方程，求解时间长，又因为自动调整臂的失效数据比较大，具有较大难度。最小二乘法求解相对比较简单，可简便地求得未知的数据，使这些求得数据与实际数据之间误差的平方和最小。为了精确评估三参数威布尔分布的3个参数，本文先假设位置参数N0已知，利用最小二乘法及平均秩的增量公式求出形状参数m和尺度参数Na，然后利用最大相关系数优化法算出位置参数N0。

3.1 最小二乘法

最小二乘估计[13]是估计线性函数中的未知参数,是威布尔分布参数估计的一种较好的方法。

对于式(3),将其左右变形，两边取自然对数得:

(7)

则A=m，B=-mln(Na-No)

则式(7)化为Y=AX+B

在威布尔分布的最小二乘估计中,为求得一条偏差最小的回归直线和符合实际最好的回归系数估计值,关键的是要提高经验分布函数的精度。

3.2 平均秩增量法

经验分布函数在可靠性数据分析中占有重要地位,以往的计算方法是通过近似中位秩公式或直接查中位秩表得到,误差较大。因此，统计学家经过长期的实践总结出如下的计算平均秩的增量公式:

(8)

式中,n为样本量；k为所有设备的排列顺序号,按故障时间和删除时间的大小排列；i为故障设备的顺序号；Ai为故障设备的平均秩次;Ai-1为前一个故障设备的平均秩次Ai。有了新的平均秩次,则:

(9)

3.3 最大相关系数优化法

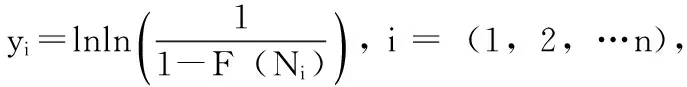
x与y间的相关系数R(x,y)为:

(10)

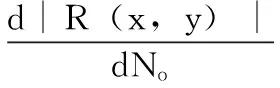
利用最小二乘参数估计法和最大相关系数优化法,拟合出三参数威布尔分布模型的回归直线,利用MATLAB计算得到威布尔分布的3个参数。

4 实验分析

本文选取25只同种型号的瀚德自动调整臂(出厂寿命值为50万次)，分别进行60万次的疲劳破坏性试验，试验装置图如图3所示。疲劳试验的实施严格按照城市客车外置式制动间隙自调臂国际标准CJT 242-2007进行，加载额定输入力矩为1020 N·m。自动调整臂疲劳试验台的模拟制动系统加载装置是完全按1:1的比例关系仿照公交客车制动系统设计而成，用于模拟汽车制动的真实环境，可减小实验环境的各项误差。疲劳试验装置结构图和实物图如下。在规定应力下，制动气室产生推力，推动自调臂的臂体转动一定的角度，使制动力以力矩的形式传递给 S 型凸轮轴，控制制动衬片作平面内的正弦往复运动，与制动鼓共同起到制动的作用。

图3 疲劳试验装置结构图

自动调整臂出现损坏情况时，现场记录其出现失效时候的实验次数即寿命值，并将试验完成的自动调整臂拆除，统计自动调整臂各零部件的损坏情况。部件失效表1按故障发生时的应力次数的大小排序。

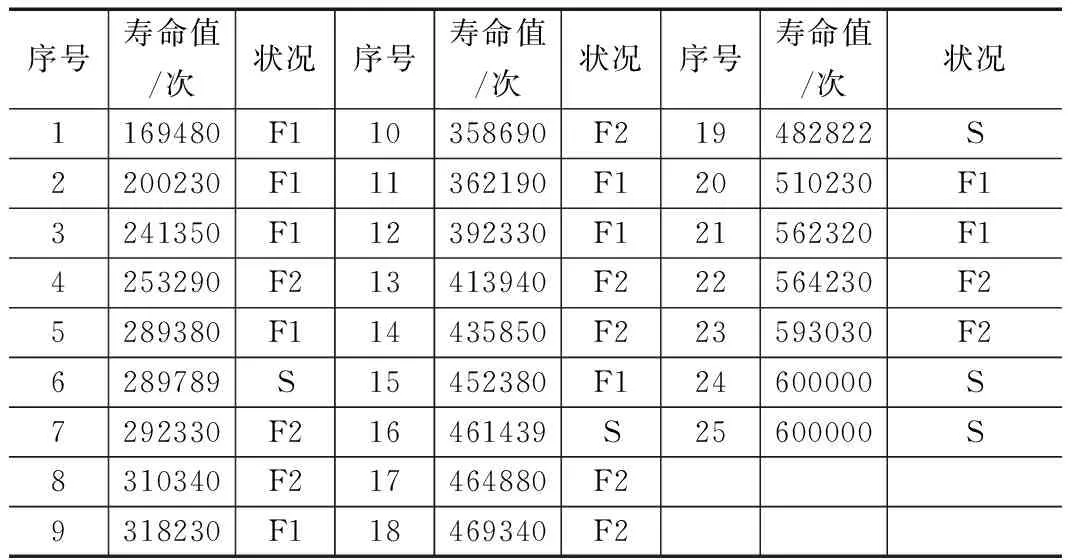
表1 部件失效次数表

注:F1表示矩形压簧故障数据; F2表示螺旋压缩弹簧故障数据; S表示删除数据

表1中的数据包括故障数据和删除数据,其中,删除数据包括未发生故障数据或由于某种原因中途撤离的自动调整臂的数据。本文先去掉删除数据,之后将发生故障的自动调整臂重新按照故障发生时的次数排序,建立威布尔分布模型,通过平均秩增量法,由式(8)、(9),分别计算故障调整臂的平均秩增量和经验分布函数值,如表2中的第4列和第5列所示。根据实验结果可知，矩形压簧和螺旋压缩弹簧是影响自动调整臂失效的主要因素。当对矩形压簧进行分析时，由螺旋压缩弹簧引起的故障可作为中断信息。同理，对螺旋压缩弹簧进行分析的时候也是如此。

疲劳试验结果统计发现，自动调整臂的一些零部件发生不同程度的失效。其中，矩形压簧的失效表现为表面点蚀、塑性变形、疲劳断裂等现象，而螺旋压缩弹簧则出现弹力不足、恢复不到位、卡牢等塑性变形失效现象，其余零部件的失效现象不明显，文中暂时不考虑。各个零部件的失效与否具有相对独立的特征，属于竞争失效的范畴。根据平均秩增量法，可分别计算矩形压簧及螺旋压缩弹簧的寿命分布关系，寿命分布表如表2，表3。

表2 矩形压簧寿命分布计算表

表2中的第6列和第7列是根据平均秩增量法及矩形压簧的疲劳寿命计算得到的坐标值,通过最小二乘估计法拟合出回归直线,如图4所示。

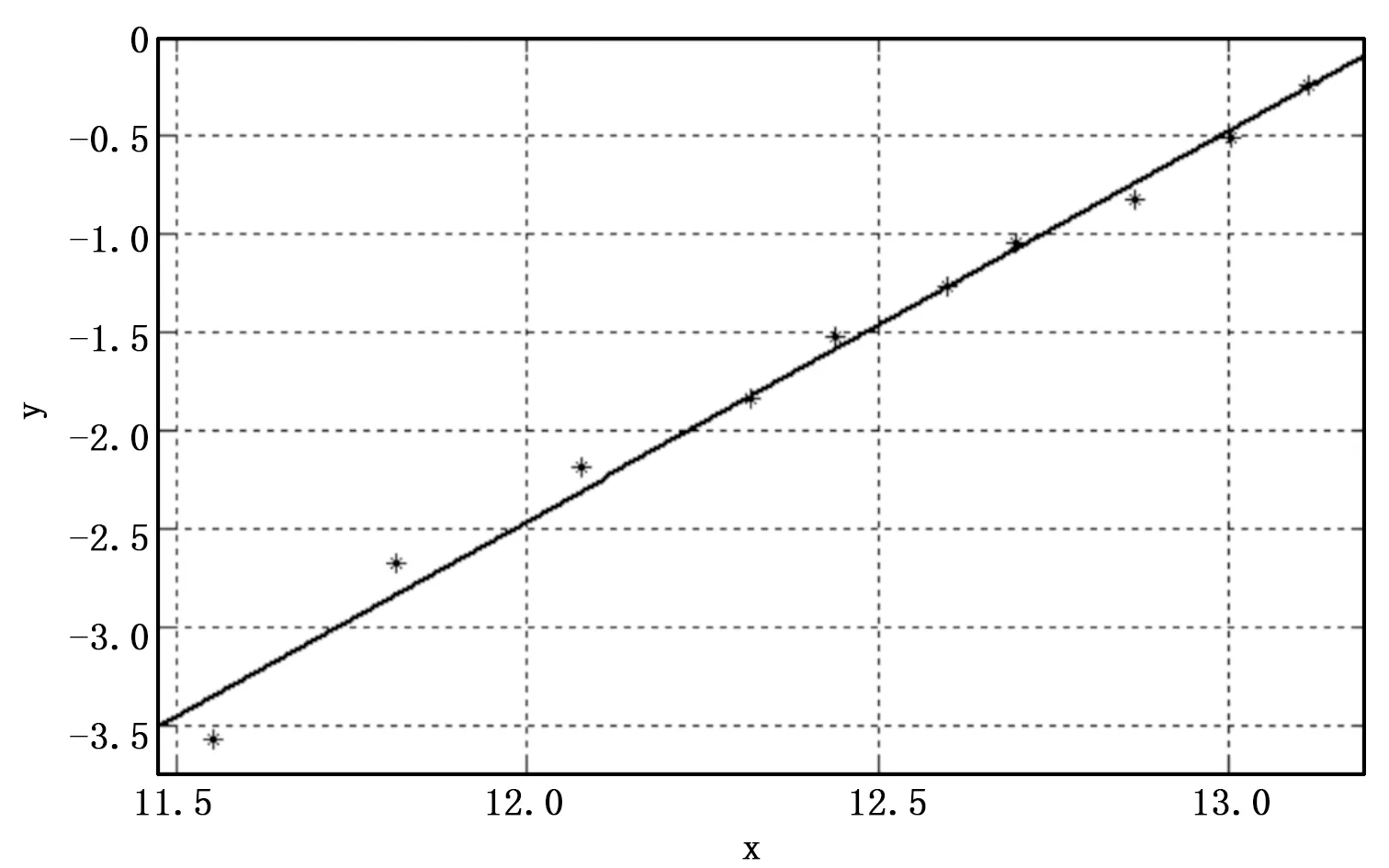
图4 最小二乘拟合图

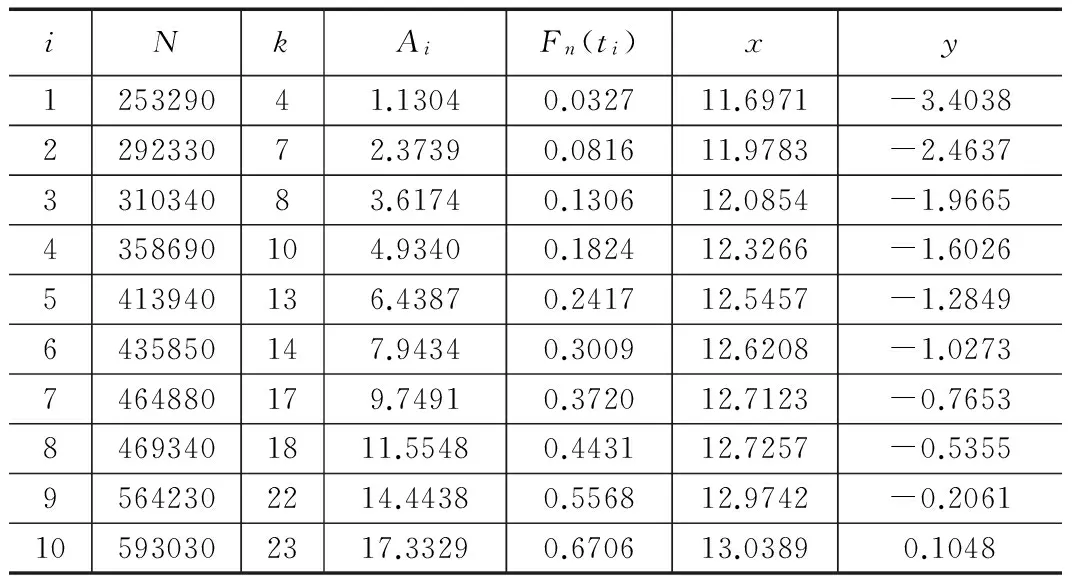
表3 螺旋压缩弹簧寿命分布计算表

图5为最小二乘估计法拟合出的回归直线,其x和y的坐标为表3中的第6列和第7列。

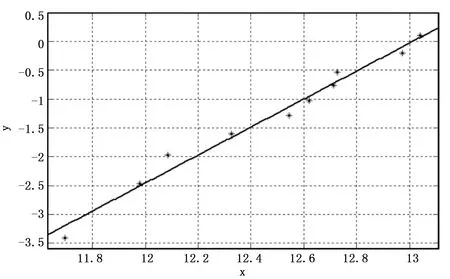
图5 最小二乘拟合图

根据图4、图5可以看出，试验值均匀分布在直线两侧，曲线的拟合精度高，利用最小二乘法评估威布尔分布的参数值的方法合理可行。

根据螺旋压缩弹簧和矩形压簧的寿命值，通过平均秩增量公式、最小二乘法以及最大相关系数法可计算出矩形压簧的寿命分布形状参数m=2.115 6，尺寸参数Na=600 113，位置参数N0=65 369。螺旋压缩弹簧的寿命分布形状参数m=2.387 6，尺寸参数Na=585 015，位置参数N0=133 069。自动调整臂的威布尔分布参数已求出,根据公式(5)，公式(6)可知自动调整臂的失效率函数和可靠度函数分别是:

(11)

(12)

根据所求的形状参数m，可知其都大于1，所以调整臂符合威布尔分布的耗损故障期,计算调整臂出厂次数的可靠性，即N=5×105次时调整臂的可靠度。

根据调整臂的可靠度函数，公式(12)可得:

R(N)=11.76%

由计算得到的可靠度,可以预测出当自动调整臂工作5×105次时,可靠度很低,安全性差，因此自动调整臂在使用达到其规定的次数后要及时检修或者替换，方可保证汽车行车过程的安全可靠。

5 结论

本文结合竞争性故障模型对自动调整臂的服役可靠性进行分析，通过三参数威布尔分布函数以及最小二乘法的参数估计可知，自动调整臂的寿命服从威布尔分布的损耗故障期。结果表明，自动调整臂的失效主要是由于螺旋压缩弹簧以及矩形压簧的累积损伤造成的。从拟合的回归直线可看出,通过平均秩增量法得到了精确的参数估计值，评估方法具有合理性。

[1] 江文松.汽车自动调整臂失效检测技术研究[D].杭州:中国计量学院,2014.

[2] 凌 丹,何俐萍,许焕卫，等.基于威布尔分布的疲劳剩余寿命可靠性预测方法[J].机械设计,2011,28(7):50-53.

[3] 凌 丹.威布尔分布模型及其在机械可靠性中的应用研究[D].成都:电子科技大学,2010.

[4] 顾梦元.威布尔分布与正态分布两种条件概率密度曲面比较研究[D].北京:北京工业大学,2014.

[5]MurthyDNP,XieM,JiangRY.WeibullModels[M].NewYork:Wiley,2003.

[6] 罗 哉,江文松,陆 艺,等.汽车自动调整臂螺旋压缩弹簧的失效建模[J].中国机械工程,2013,24(12):1596-1599.

[7] 郭永基.可靠性工程原理[M].北京:清华大学出版社,2002.

[8] 陆 山,吕鸿雁.小子样零构件可靠寿命零故障试验评估方法[J].机械强度,2006,28(3): 411-414.

[9] 王金武.可靠性工程基础[M].北京:科学出版社,2013.

[10] 赵 宇.可靠性数据分析[M].北京:国防工业出版社,2011.

[11] 洪延姬,王志魁,李俊美,等.寿命服从威布尔分布产品相关失效数值分析[J].装备指挥技术学院学报,2002,13(5):33-35.

[12] 金 星,陈景鹏,文 明,等.威布尔分布产品参数估计极大似然优化方法[J].装备指挥技术学院学报,2003,14(5):46-48.

[13] 王桂萍,贾亚洲.MTBF分布模型的案例分析[J].吉林工程技术师范学报,2005,21(3):20-24.

Service Reliability Research of Automatic Brake Adjuster Based on Weibull Distribution of Three Parameters

Luo Zai, Wang Yan, Wang Lanjing, Liu Hui

(China Jiliang University, Hangzhou 310018, China)

As a key component of the auto-brake system, the automatic brake adjuster is related to the safety of vehicle driving. The possibility of failure of the automatic brake adjuster is analyzed by fatigue test. The results show that the rectangular compression spring and the helical compression spring are the key factors affecting the failure of the automatic brake adjuster. By using MATLAB, it can be seen that the fatigue life of the automatic brake adjuster obeys the Weibull distribution of three parameters, combining with competitive fault model to analyze the reliability of the automatic brake adjusters. Based on the model, the least squares method and the maximum correlation coefficient method are used to analyze the reliability of the automatic brake adjuster. The life data in the experiment were used to estimate the parameters. The example shows that the method is simple, convenient and practical, and the Weibull distribution of the competitive fault model can accurately reflect the statistical properties of the data of the automatic brake adjuster fatigue test, which is of good engineering application value.

automatic brake adjuster; Weibull distribution; competitive fault model; least square method

2016-10-08；

2016-11-11。

浙江省自然科学基金(Y15E050053)。

罗 哉(1979-)，男，四川遂宁人，教授，硕士研究生导师，主要从事汽车零部件检测与精密测试技术方向的研究。

1671-4598(2017)03-0234-03DOI：10.16526/j.cnki.11-4762/tp

TH

A