慢下来，才能化得开

陈秋霞

摘 要：把课堂上生成的问题转化为学生发展的机会，让学生在学中思，在思中悟，在悟中得，以此提升思维水平，有效解决学生的认知冲突，达到对知识的深刻理解和思维的深度发展。

关键词：捕捉；发展；问题

镜头一：捕捉“疑点”，在思辨中发展

在学完多边形的面积计算后，为帮助学生及时巩固新知，提高学生分析问题、解决问题的能力，我出了几道习题。其一是：一个长方形操场，长50米，宽40米，扩建后长和宽分别增加5米，问扩建后操场面积增加了多少平方米？

马上出现了方法一：50×40=2000平方米

55×45=2475平方米

2475-2000=475平方米

还没等前面的同学说完，机灵鬼李×就嚷开了：““老师，用不着那么麻烦，只要5×5=25平方米就行了。”不少人立即响应，并且對李×另辟蹊径的简单解法十分赞赏，我也有种“柳暗花明”的感觉。正想开口，不知是谁冒出了一句“好像……好像有些不对劲啊！”话音未落，出现了几个附和的声音：“对呀！怎么结果不一样呢？按理不管用什么方法结果应该一样的啊？可李×的好像也没错呀。”教室里一下子凝滞了，大家都把目光聚焦到了我身上，我表扬了仔细观察敢于怀疑的态度，微微一笑顺势说：“结合题意，自己动手，想办法来证明自己的方法是正确的。”同学们纷纷埋头推敲了起来。

时间一分一分的过去了，终于看到有同学举手了，一位学生说：“方法一肯定没问题，扩建后的面积减去扩建前的面积，问题肯定出在方法二上，问题在哪呢？”教室里一片寂静，又过了几分钟，忽然发出了一个声音：“我知道了，我知道问题在哪了？”“我画了一个图。”他扬了扬手中的草稿，脸上由于激动涨得通红。

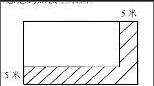
如下图，我示意他到黑板上来画。

“我发现扩建上去的不刚好是正方形，是上面的阴影部分，所以不能用5×5计算。”“哦，对呀！”“我怎么没想到呢？”下面的同学茅塞顿开，同学们向他投去了赞许和敬佩的目光。的确通过画图，可以清晰地看出长和宽增加与增加面积之间的关系。我由衷地说：“当我们理不清题意的时候，动手画图是一种不错的选择！感谢你的智慧分析，感谢李×同学带给我们的精彩。”

从上面的例子不难看出，学生的思维在很大程度上带着随意性。当学生“与众不同”的解法出现时，要尊重和激励学生独特的思维方式，慢下来，留给孩子充足的时间，留给孩子思考、想象的空间。让学生多一些自主探索知识的经历与体会，多一些与同学交流的机会和体验。这不就是我们一直念叨着的核心素养吗？虽然这题花了足足10分钟，我觉得很值！相信不管过了多久，孩子们都会记得今天的苦思冥想，茅塞顿开。

镜头二：捕捉“误点”，在验证中发展

教学完平均数一课后，我出了几道练习题，其一如下：

有水果糖4千克，每千克3.2元，奶糖5千克，每千克4.8元，芝麻糖11千克，每千克6.4元。将这些糖混合成什锦糖，这种什锦糖平均每千克多少元？

练习时，大部分学生列式：（3.2+4.8+6.4）÷3=4.8元，表面上看似乎合乎题意，把3种糖的价格和除以种数3就是单价。短暂的停顿之后没有听到反对的意见，如果直接告诉学生正确答案，学生对求平均数不能有深切的体会。“让我们想办法来验证一下吧，”几分钟后，有学生出示了这样2个算式：

4.8×（4+5+11）=96元

4×3.2+5×4.8+11×6.4=107.2元

有几个孩子已经眉头紧锁，发现了两次的总价不一样，显然平均每千克4.8元是错误的。周××首先发现了其中的问题，他嘀咕道：（3.2+4.8+6.4）÷3=4.8元是求出三种糖单价的平均数，而这里三种糖的重量不同，就不能用只求单价的平均数的方法来做了。我追问：“那什么情况可以通过（3.2+4.8+6.4）÷3=4.8元来计算呢？”“当这3种糖重量相等的时候上面这个算式是成立的，”胡××迫不及待的补充。

通过验证这一策略，学生利用错误答案计算出总价与原题中的总价不相符，引发了认知冲突，从而引发学生主动反思，去找症结所在。再通过追问什么情况下用（3.2+4.8+6.4）÷3=4.8元来计算是正确的，进一步打开了思维的阀门。“那本题该怎么解呢？……”孩子们很快找到了数量关系，每种糖的总价÷总重量=什锦糖单价，列式为：

（4×3.2+5×4.8+11×6.4）÷（4+5+11）=5.36元

再次验证：5.36×（4+5+11）=107.2元，与原总价相符，结果正确。

把课堂上生成的问题转化为学生发展的机会，让学生在学中思，在思中悟，在悟中得，以此提升思维水平，有效解决学生的认知冲突，达到对知识的深刻理解，使课堂妙趣横生。

作为教师，不仅要提高自己捕捉生成信息的能力，还要提高判断信息价值的能力。对学生的错误，要根据情况区别对待，如对学习习惯存在的问题可以在个体中处理或对其他学生进行提醒。对于共性的知识层面的错误要面向集体共同交流，如案例二，大部分学生把三种糖的单价和除以种类三计算得出的是三种糖单价的平均数，忽略了每种糖重量的不同，通过验证、发现、再思考解决。对于有思维价值或对学习新知有帮助的错误，要挖掘其原因，引导学生共同解决，如案例一，使学生在自我不断澄清的过程中获得发展。正如郑毓信教授说的帮助学生学会思维，并能逐步学会想得更清晰、更深入、更全面、更合理，由“理性思维”逐步走向“理性精神”。长此以往，还怕我们的孩子不会发展吗？

参考文献：

[1]付娜.小学数学探究学习实践研究[D].东北师范大学，2012.

[2]冯洋.华应龙小学数学教学智慧研究[D].渤海大学，2014.

编辑 鲁翠红