优先关联的Web日志数据逼真生成算法①

丘志鹏, 肖如良, 张 锐



优先关联的Web日志数据逼真生成算法①

丘志鹏, 肖如良, 张 锐

(福建师范大学软件学院, 福州 350117) (福建省公共服务大数据挖掘与应用工程研究中心, 福州 350117)

字段关联的构建方法是Web数据逼真生成中的困难问题. 提出一种基于MIC的字段优先关联的Web数据逼真生成算法. 该算法与现有的方法完全不同: 首先, 提取真实Web日志数据集中相应字段间的MIC系数; 然后, 结合字段的重尾特性, 采用SE分布对字段的重尾性进行建模; 最后, 建立字段关联模型, 模拟出真实数据集中的字段间依赖性, 从而逼真生成目标数据集. 实验表明, 生成的数据集能够保持合理的字段间的均衡性以及节点间的相似性.

字段关联; 数据生成; MIC系数; 重尾

合理分析Web日志数据的字段内容, 有助于对其领域系统的构建及测试, 然而Web日志数据通常达到TB甚至PB级别, 极其耗费网络资源, 并且数据中用户行为及相关物品属性等相关字段内容涉及隐私信息, 因此, 企业及政府等机构极少愿意分享其数据供研究人员使用. 随着互联网规模的不断扩大, Web日志数据中重尾现象也越发普遍, 各个字段间的关联变得愈加复杂, 生成具有真实数据特性的数据集极具难度. 因此, 构建一个可模拟出真实字段间关联关系的数据生成算法成为众多科研工作中模拟数据来源的基础, 也是本文研究的重点.

现有的数据生成算法的研究主要分为时间字段相关性质的研究与非时间字段相关性质的研究两个方面. 前者主要应用于网络流量预测、时序分析等方面, 现已较为成熟, 有相应的商用与科研软件供研究人员使用, 如OPNET; 而后者主要在于对字段分布特性的数学建模及字段间关联研究, 主要应用于特定的研究项目中, 需要根据不同业务场景进行逼真生成, 复杂度高, 主要代表性工作有加拿大萨斯喀彻温大学Busari提出的proWGen[1]数据生成器, 通过分析Web用户行为字段值分布情况, 用Zipf-like分布刻画字段重尾性[2]进行数据生成, 采用多参数的机制, 使得该生成器具有良好的扩展性, 能应用于Web服务器的压力测试及缓存性能研究. 缺点在于: proWGen对字段关联仅采用简单的正/负相关的方式实现, 难以逼真生成实际中复杂多样的数据.

随着互联网数据量的爆炸式增加, Zipf-like已经不再适用于描述具有重尾特性的Web数据分布, 文献[3]指出采用SE分布描述Web数据的重尾性更加合理. 若采用Zipf-like进行数据生成, 对于生成数据所应用的系统而言, 其测试性能评估上会存在高估的结果, 与真实数据情况对比有较大的误差, 意味着生成了不可靠的数据. 所以目前非时间字段相关性质研究仍处于成长阶段. 本文主要以非时间字段相关性质研究作为主要工作.

针对以上问题, 本文提出了一种基于MIC的字段优先关联的Web日志数据逼真生成(Simulate Generating Web Log algorithm using fields’ priority relevance based on maximal information coefficient, SGWL)算法. 该算法与现有的方法完全不同, 通过利用Web日志数据特征进行参数提取, 采用SE分布代替Zipf-like分布对字段重尾性进行刻画. 然后对数据字段关联提出一种全新的模型(基于MIC的字段优先关联模型)代替传统的正/负相关模型, 进行指导关联. 通过该算法生成的数据, 不仅在整体上能拟合一个逼真的分布趋势, 在局部上也能够准确刻画字段重尾性并保持合理的字段间的均衡性以及节点间的相似性, 可应用于 Web数据驱动的软件过程.

1　相关工作

目前, 国内外已有大量的仿真数据生成研究. 按其是否与时间因素相关可分为二个类别: 其一, 与非时间字段性质相关的研究; 其二, 与时间字段性质相关的研究.

(1) 非时间字段相关性类型的研究主要涉及非时间相关字段的建模及字段间关联研究, 例如字段值出现次数分布建模、重尾性刻画等. 通过已有Web数据作为驱动, 对其进行数学建模, 从而来模拟生成新的数据. 中科院计算所詹剑锋研发的可扩展大数据生成器BDGS[4]在生成量、速率、多样性、真实性这四个角度进行仿真数据, 能够自定义生成结构化、半结构化、非结构化数据并能保持数据的重尾性, 但是其缺陷在于: 字段关联模型单一、缺乏物理意义; 新加坡国立大学Tay[5]通过研究照片评论数据, 指出字段关联关系在数据生成中的重要性. 在Tay的研究工作中定义了五种数据类型, 实际上这种做法存在一定的局限性, 五种类型不足以囊括复杂多样的真实数据; proWGen数据生成器采用多参数可调机制, 运用数学模型建模可生成具有Web访问特征的数据. 该方法具有较大的灵活性, 可以较为逼真的模拟单列Web数据字段, 但是在多字段数据生成中仅仅采用正/负相关的方式进行仿真, 不足以描述Web数据中不同字段属性的复杂关系; 加拿大多伦多大学Rabl设计的PDGF[6]数据生成器, 目前是TPC-DI(数据集成评测系统)的专用数据生成器, 已经被大数据测试基准BigBench广泛使用, 但是该生成器只供特定数据进行生成, 其扩展性较为一般; 工业界现有的数据生成器Red Gate[7]、DTM[8], 可高速生成与真实业务数据相似的数据, 然而, 工业界的数据生成主要依托于相关的业务, 由于这类生成器具有通用性, 也意味着无法根据真实数据的特性随意修改生成字段间的关联.

(2) 时间字段相关性类型的研究, 需要为时间属性字段建模, 通过模拟时间相关属性特征(如网络流量自相似性、长相关性、多分形性)来生成Web数据. 其中包括以浙江大学尹建伟研发的BURSE[9]为代表的工作负载数据生成器, 重点模拟数据的周期性、突发性特征来实现Web数据的自相似性; 法国凡尔赛大学Laurent[10]主要通过研究天气数据的时间序列, 在不同时间尺度上依赖于多分形理论进行相应数据仿真生成; 美国新泽西理工学院Ansari[11]研究了基于FARIMA的MPEG视频流量建模问题,采用 FARIMA过程作为自相似流量产生器, 对MPEG中的I、P和B帧的自相关结构进行建模, 从而完成数据生成. 此外, 时间字段相关性质研究领域也具备较为成熟的产品用于数据生成, 加拿大西蒙菲沙大学Michael[12]收集了蜂窝数字包数据网络(CDPD)中的业务数据并对运用工具OPNET建模和仿真分析. 以上的这些时间字段相关性质研究成果, 均有强力的学科理论、技术模型支撑, 其涉及到自相似网络业务ON/OFF模型、时间序列分析FARIMA模型等, 并且也有较为成熟的产品供研究人员使用, 商用软件有OPNET, BONeS和COMNET III, 科研用软件有NS2和SSF NET. 而非时间字段相关性质研究的数据生成方法, 目前并没有一个通用的商用软件供研究者使用, 并且现有的数据生成器中依然局限于简单的数据分布与粗糙的字段关联, 没有一个合适且较为完备的模型来指导非时间字段相关性质研究数据生成中字段关联的问题.

综上所述, 数据生成器的时间字段相关性质研究已趋于成熟, 而非时间字段相关性质研究中仍存在许多需要急于解决的困难问题. 本文重点对数据生成的非时间字段相关性质研究进行相关改进工作. 通过运用SE分布来对具有重尾现象的Web字段值出现次数进行刻画, 在所需关联的字段间用MIC系数作为关联度的描述, 建立全新的关联模型, 进而使生成的数据更具有可靠性, 从而达到逼真生成的目的.

2　理论基础

2.1 重尾数据的分布

2.1.1 Zipf-like分布

大数据背景下, Web日志数据中部分字段分布呈现出幂律分布的特性, 也就是人们常说的长尾现象, 本文中统一称为重尾性. Zipf-like分布又称为类齐普夫分布, 通常用于描述具有重尾性质字段的分布, 本节图示以Movielens-1m数据集为例, 以排名位序值(Rank)作为X轴, 以出现次数(Times)t作为Y轴, 如图1所示userID字段值出现次数(又称为用户活跃度)表现出重尾性, 在传统方法中通常使用Zipf-like分布来对其进行刻画.

图1　用户活跃度分布情况

假设一个数据集D中某字段A服从参数为的Zipf-like分布, 那么对其字段值所出现的次数统计进行降序排列, 序列第的字段A, 其出现的次数t满足式(1):

其中为数据集的总记录数, 参数的表达如式(2)所示:

若数据集D中某字段的所有值出现次数服从Zipf-like分布, 那么根据对象出现次数降序排列, 在坐标系中, 以排名位序值(Rank)作为X轴, 以出现次数(Times)t作为Y轴, 分别对X轴、Y轴上的对应所有数据进行取自然对数处理, 那么应当呈现出一条直线. 如图2可发现, 用户活跃度在双对数坐标系下并非呈现一条直线, 说明用户活跃度并不服从Zipf-like分布.

图2双对数坐标系下用户活跃度分布情况

2.2.2 SE分布

SE分布(Stretched Exponential Distribution), 中文全称为广延指数分布, 最早由Kohlrausch于1847年研究发现, 适用于描述不同复杂系统的动态衰减现象, 其中包括自然、经济、互联网等领域. 美国俄亥俄州立大学张晓东[3]对不同Web系统的用户行为日志数据进行分析, 发现Zipf-like分布不适合描述Web日志行为数据的重尾性, 而SE分布能对其进行很好的刻画. 说明该分布适用于描述幂律模型无法准确刻画的情况.

式(3)表示SE分布的概率密度函数:

累计分布函数如式(4)所示:

其中为广延参数, 其参数范围在(0, 1),x为尺度参数.

为了方便描述, 我们约定将X轴上的对应所有数据进行取自然对数处理, Y轴上的对应所有数据进行取原值的次幂处理, 这样得到的坐标系称为SE坐标系. 若数据集D中某字段的所有值出现次数服从SE分布, 那么根据对象出现次数降序排列, 在坐标系中, 以位序值作为X轴, 以出现次数t作为Y轴, 再将X、Y的值转化置SE坐标系中, 那么应当呈现出一条直线. 如图3, 可以清楚的看出用户活跃度在SE坐标系下呈现一条近似直线, 说明用户活跃度服从SE分布.

图3 SE坐标系下用户活跃度分布情况

采用公式(5)对该直线进行描述:

2.2 字段关联性度量

记录是由若干个字段组合而成, 而字段间必然存在着某种关联. 为了能准确量化描述两个字段间的关联性, 研究者们提出了pearson系数、spearman系数、核密度估计(KDE)、互信息等度量标准. 这些度量方法复杂、不适用非线性数据, 缺乏普适性、健壮性低等问题, 难以适用于数据生成算法中. 为此本文采用MIC(The Maximal Information Coefficient)系数作为字段关联性度量.

2011年, Reshef[13]在Science首次提出MIC系数, 中文又称为最大信息系数. 该系数是在互信息的基础上衍化而来, 能对不同类型的关联关系进行评估, 其范围为[0,1], 且具有对称性、良好的普适性和公平性. 如果变量与独立, 则MIC(,)=0; 如果与之间具有确定的关系, 则MIC(,)=1, 此时不存在任何噪声影响.

计算方法主要是通过对变量对(,)中所有样本点的构成的散点图进行划分, 利用动态规划的方式计算并搜索不同划分方式下所能达到的最大互信息值. 最后, 对最大互信息值进行标准化处理, 所得结果即为MIC, 记作e. 记’为给定数据集,和分别表示在X和Y变量轴上的划分份数,为变量对(,)的样本容量, G表示某种划分. 因此在划分G下等(×)轴划分的最大互信息为式(6):

标准化处理得到的特征矩阵如式(7)所示:

最终得到的MIC值如式(8)所示:

其中()为网格划分细度, 通常取值为0.6, 以上方法步骤简称MINE方法.

由式(8)可以发现, MIC随着网格划分细度的变化而变化, 当样本容量越大的时候估计值也越准确, 这适用于当前大数据的时代背景. 表1列出四种相关系数的应用对比, 由表1可知MIC系数具有适用范围广、计算复杂度低, 鲁棒性高, 标准化结构特性. 因此, 本文算法采用MIC作为字段关联度参考.

表1 四种相关系数优劣对比

注: L—低; M—中; H—高; Y—是; N—否.

3　基于MIC的字段优先关联模型

假设要生成由两列字段组成, 共计条记录的日志数据集, 其中字段名分别用A、B表示. 令字母S表示为集合, 那么字段A对应的值所在集合SA={A,A,A…A}, 共有种取值; 字段B对应的值所在集合SB={B,B,3…B}, 共有种取值. 每条记录的形式为{A,B}(1≤≤,1≤≤). 令字母t代表次数, 则字段A值A出现的次数为t次,字段A中所有值分别出现次数构成集合S, 字段B中值B出现的次数为t次, 字段B中所有值分别出现次数构成集合S, 且满足式(9)表示字段A所有值出现次数累加和等于字段B所有值出现次数累加和等于日志数据集总记录数.

对于数据生成而言, 首先分别对字段的所有值出现次数的集合进行建模, 根据章节2.1的方法, 得到出现次数降序排列的集合S与S. 然后累积分布函数(), 其中表示字段值出现次数的排名位序. 以A字段为例, 累积分布函数具体如式(10), 到该步便完成字段建模的步骤.

记录是由字段组合而成, 在完成字段建模之后, 需要将两个字段进行关联操作, 进而形成一条完整的记录. 关联操作即为取集合SA与SB笛卡尔积的一个元素的过程. 假定符号ξ表示(0,1)上均匀分布的随机数, 字母r表示关联取值数, 则在生成一条记录时, 首先生成随机数ξ, 令ξ=p(), 通过式(10)的逆函数解析式,计算可得唯一的实数位序, 根据位序与字段值映射关系, 求得字段值A. 然后, 根据AB字段间的相关性, 通过关联模型计算得到r, 令r=B(), 同理可得字段值B, 即得到记录{Ax,B}.

关联过程存在三种情况, 分别为正相关、负相关与零相关, 其中正相关表示自变量增长, 因变量也跟着增长; 负相关表示自变量增长, 因变量反而减少; 因变量的增减与自变量的增减无关, 相互独立. 现阶段数据生成算法中主要使用关联模型分为正相关模型与负相关模型, 其中正相关模型为r=ξ, 负相关模型为r=1-ξ, 该模型的不足之处在于关联度量简单, 不具备的物理意义, 且未考虑字段间零相关情况. 因此, 本文提出一种基于MIC的字段优先模型PRF(the Priority Relevance of Field based on maximal information coefficient, PRF). 令表示经过PRF模型得到的关联取值数, 且由优先关联部分与独立部分组合而成. 正相关PRF模型如式(11)所示:

负相关PRF模型如式(12)所示:

其中∈[1,],∈[1,], 参数e∈[0,1]为字段A与字段B之间的MIC系数, 用于衡量字段间相关程度, 在模型中的物理意义表示优先关联部分所占比例.表示随机字段值A出现次数的累积分布概率()./表示在B字段中个取值内, 随机选取第个值作为字段值的概率. 令,ξ=/分别带入式(11)、式(12), 化简得到式(13)、式(14).

若字段间存在关联, 模型优先采用ξ对字段B进行关联取值, 若字段间相互独立, 则重新生成随机数ξ, 进行关联取值. 当时, 说明字段A与字段B存在线性相关关系, 表示每个字段A的值都关联着在各自累积分布函数()下相同累积概率的字段B的值, 以正相关模型为例, PRF模型转化为. 当时, 说明字段A与字段B相互独立, 表示每个字段A的值都与字段B的值不存在关联, 呈现随机关系. 以正相关模型为例, PRF模型转化为. 当时, 优先关联部分所占比例为e, 独立部分所占比例为(1-e), 通过两部分的和, 根据式(11)计算得出, 以作为字段B中某值的累积概率, 从而可以求出字段B的值, 最终完成一次字段A与字段B的关联.

PRF模型具有一般性与明确的物理意义, 以MIC系数作为主要参考, 能合理的描述数据间的关联情况, 适用于大部分数据生成算法中的字段关联步骤.

4　基于PRF的Web日志数据生成算法SGWL

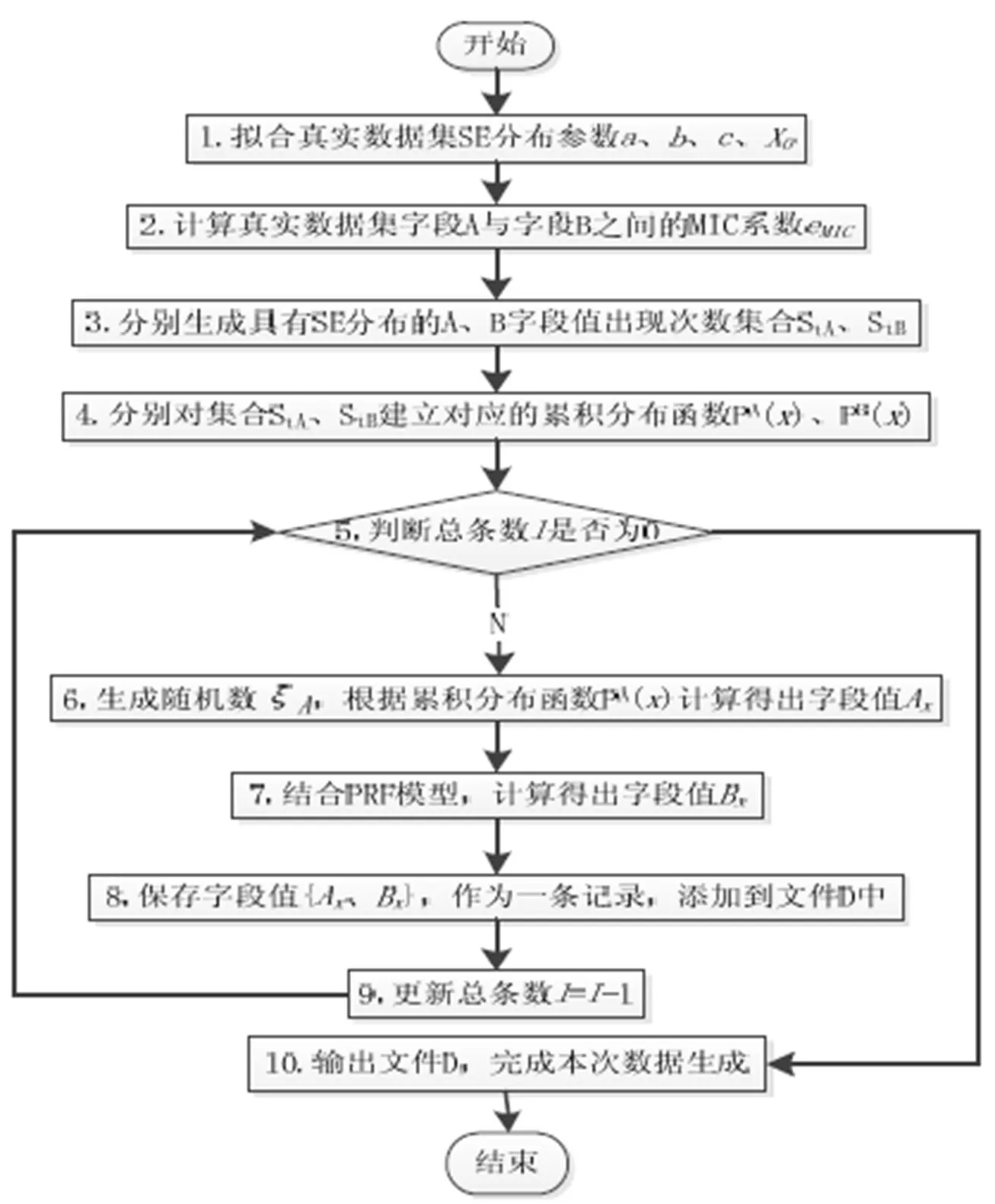
图4 基于PRF模型的Web日志数据生成算法SGWL

本文提出一种基于PRF的Web日志数据逼真生成算法SGWL. 该算法通过提取真实数据集的相关参数, 利用SE分布模拟具有重尾性质的字段值出现次数集合, 在数据生成过程中根据PRF模型完成字段关联, 每次生成完一条记录之后对总条数进行更新, 从而达到控制生成记录总量的目的. 算法描述如图4所示.

在图4 SGWL算法流程中, 步骤1至步骤2为Web日志数据字段特征提取过程, 步骤3至步骤4表示对字段进行建模, 步骤6至步骤8为生成一条完整记录的过程, 其中步骤7表示字段关联.

5　实验结果与分析

5.1 实验数据集介绍

在生成Web日志数据结束之后需要测评仿真数据集的可靠度, 采用真实数据集作为参照比对. 实验采用四个不同领域具有代表性的数据集进行实验分析, 旨在验证SGWL算法的一般性, 其分别是Movielens-1M电影评分数据集、NASA网络请求数据集、Epinions社会网络数据集和Xiami音乐用户行为数据集. 其中 MovieLens 1M为6040个用户对3952个电影产生的1000209条评分记录; NASA为54770个请求节点对8937个路径产生的1048576服务日志数据记录; Epinions为40163个用户对139738个物品产生的664823条评分记录; Xiami为162273个用户对8377首歌曲产生的11098957条行为记录, 其统计结果如表2所示.

表2 四个数据集基本统计结果

5.2 评估指标

2.巴基斯坦政府做出了巨大的努力，尤其在路线选择上。巴基斯坦政府在规划经济走廊路线时充分考虑了各方的利益诉求，推出了多路线方案，满足各方的利益诉求，从根源上减少某些“变相恐怖主义”的袭击。

5.2.1字段均衡性指标: 基尼系数

基尼系数(Gini Coefficient)[13]是意大利经济学家基尼于1992年提出, 定量测定收入分配差异程度. 基尼系数是比例数值, 在0和1之间, 是国际上用来综合考察居民内部收入分配差异状况的一个重要分析指标. 假定一定数量的人口按收入由低到高排序, 分为人数相等的m组, 从第1组到第组人口累计收入占全部人口总收入的比重为其计算方法如式(15)所示. 按照联合国有关组织规定: 0.2表示绝对平均, 0.3-0.4表示相对合理, 0.5以上表示严重不均衡. 而如今, 基尼系数也可以用来测度各种意义下的资源分配均衡度. 正因为数据生成的时候需要对字段值出现次数进行建模, 同理基尼系数也适用于评估字段值出现次数的均衡性, 可以通过式(15)计算Gini系数.

5.2.1节点相似性指标: PA指数、AA指数

若用二分网络结构来描述数据集, 那么字段上的值即对应为网络中的节点这一概念. 节点相似性指标[14]在链路预测、节点聚类、个性化推荐方面应用都很广泛. 电子科技大学周涛[14]罗列了十五种相似性指标, 本文采用其中两种稳定性较好的指标作为实验评判标准, 分别是PA指数与AA指数. 令表示节点相似性度量,与分别表示字段值与,表示字段值,表示字段A中既关联了又关联了的字段值的集合,表示出现的次数,表示出现的次数,表示出现的次数.

PA(Preferential Attachment )指数计算如式(16):

AA(Adamic-Adar)指数计算方法如式(17)所示:

5.3 实验结果及分析

首先, 就整体层面而言, 本节选用Movielens-1m数据集与Epinions数据集作为真实数据集参考, 对具有重尾性质的字段User值出现次数分别进行Zipf-like分布刻画与SE分布刻画, 然后选取合适分布对字段进行拟合, 并计算出拟合函数与真实数据集的拟合优度^2评估拟合效果, 其实验结果如图5、图6所示, 其中点线为双对数坐标系下真实数据分布刻画, 虚线为SE坐标系下真实数据分布刻画, 实线为拟合直线.

由图5与图6, 可以看出两个数据集字段User值出现次数分布在双对数坐标系下均呈现出“胖头瘦尾“的曲线形状, 而在SE坐标系下均呈现出一条近似直线的情况, 因此根据章节2.1所述, 验证了SE分布在描述重尾特征的数据字段上优于传统的Zipf-like分布. 然后对虚线进行拟合, 通过R语言中的nls方法计算得到、值, 然后在图上绘制对应直线, 计算出虚线与实线之间的拟合优度^2. 图5中,^2=0.9748, 图6中,^2=0.9719, 均接近于1, 说明回归直线对真实数据的拟合程度很高. 总体而言, 采用SE分布的SGWL在重尾性刻画上描述要优于proWgen, 生成的数据与真实数据集更为接近, 能更准确的描述真实数据集的重尾性, 从整体上把握数据的逼真生成.

图5 Movielens-1m字段User整体分布拟合刻画图

图6 Epinions字段User整体分布拟合刻画图

在局部层面上, 基尼系数是研究字段均衡性的一个重要特征, 选用四个不同领域的真实数据集的某一字段分别采用SGWL算法与proWgen算法进行数据仿真, 最终与真实数据集通过计算其基尼系数进行字段均衡性对比分析. 实验结果如表3所示.

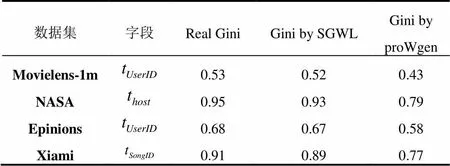
表3 真实数据集与生成数据集字段基尼系数(Gini)对比

根据表中数据可以直观的看到列“Gini by SGWL”的每一个数值都明显逼近于列“Real Gini”的值, 进一步通过数据计算可以得到SGWL生成数据的基尼系数与真实数据集的平均误差为1.5%, 而proWgen生成数据的基尼系数与真实数据集的平均误差却达到了11%, 由此说明, SGWL算法生成的数据在字段均衡性上要优于proWgen, 且适用于不同领域背景下的数据生成, 具有一般性.

最后在个体评估层面上对节点间相似性进行实验分析. 以Movielens-1m数据集作为真实数据集参考, 根据5.2.2介绍的方法, 令字段”UserID”代表字段A, 字段”MovieID”代表字段B, 在字段B中随机选取10000对节点{,}, 依次分别在真实数据集与SGWL算法生成数据集中计算对应的相似性度量, 令真实数据集中所有组成的序列为, SGWL算法生成数据集中所有组成的序列为. 实验需在坐标轴上绘制10000个散点, 其中以上所有的10000个值归一化后依次作为散点的X坐标, 以上所有的10000个值归一化后依次作为散点的Y坐标. 若两个数据集具有相同的节点相似性, 那么散点将全部散落在倾斜度为45度的实线y=x上, 偏离斜线越远则代表两个数据集的节点间相似性差异越大, 从而说明算法生成的数据越不可靠. 实验结果如图7、图8所示.

图7 PA下节点相似性对比

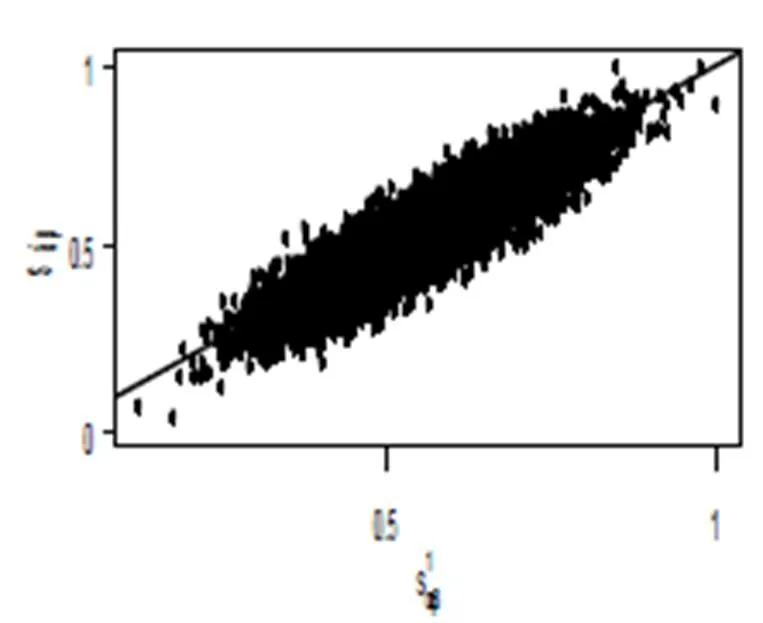
图8 AA下节点相似性对比

如图所示, 图7、图8中大多数的散点位置均落在y=x这条斜线的附近, 部分点甚至于斜线重合. 图7中真实数据PA指数与SGWL算法生成数据PA指数误差为0.18%, 图8中真实数据AA指数与SGWL算法生成数据AA指数误差为6%, 因此图7散点分布较图8更为稠密. 从而说明生成的数据能较好的保持真实数据集中节点间的相似性, 表明SGWL算法生成的数据具有一定的可靠性. 在图中7中99.8%节点对PA指数集中于(0,0.4)这个区间内, 这种情况的产生源于数据集中User字段的重尾性, 由式(16)可以看到, PA指数依赖于节点对值出现次数的乘积, 因此重尾性导致该乘积值普遍较小, 从而使得散点集中落在X坐标上(0,0.4)这个区间内. 这也进一步说明了SGWL算法能逼真刻画字段的重尾性.

6　结论

合理的字段关联是Web日志数据生成算法中的关键. 本文提出了基于MIC系数的字段优先关联的Web日志数据逼真生成算法SGWL, 该方法以SE分布代替Zipf-like分布来模拟Web数据的重尾性, 并提出一个全新且物理意义明确的字段关联模型PRF, 指导字段关联. SGWL算法可保证生成的数据集具有同真实数据集一致的字段间关联和字段值的分布, 为Web数据驱动的软件研发, 提供了可靠的逼真数据生成.

1 Busari M, Williamson C. ProWGen: A synthetic workload generation tool for simulation evaluation of web proxy caches. Computer Networks, 2002, 38(6): 779–794.

2 Sarla P, Doodipala MR, Dingari M. Self similarity analysis of web users arrival pattern at selected web centers. American Journal of Computational Mathematics, 2016, 6(1): 17–22.

3 Guo L, Tan E, Chen S, et al. The stretched exponential distribution of internet media access patterns. Twenty-Seventh ACM Symposium on Principles of Distributed Computing (PODC 2008). Toronto, Canada. August, 2008. 283–294.

4 Ming Z, Luo C, Gao W, et al. BDGS: A scalable big data generator suite in big data benchmarking. Advancing Big Data Benchmarks. Springer International Publishing, 2014: 138–154.

5 Tay YC, Dai BT, Wang DT, et al. UpSizeR: Synthetically scaling an empirical relational database. Information Systems, 2013, 38(8): 1168–1183.

6 Rabl T, Poess M, Danisch M, et al. Rapid development of data generators using meta generators in PDGF. International Workshop on Testing Database Systems. 2013. 1–6.

7 Campbell MK. SQL data generator. Sql Server Magazine, 2009.

8 Lear D, Hebbes S. Database Tools, EP1606735. 2005.

9 Yin J, Lu X, Zhao X, et al. BURSE: A bursty and self-similar workload generator for cloud computing. IEEE Trans. on Parallel & Distributed Systems, 2015, 26(3): 668–680.

10 Akrour N, Mallet C, Barthes L, et al. A rainfall simulator based on multifractal generator. EGU General Assembly Conference. EGU General Assembly Conference Abstracts. 2015.

11 Ansari N, Liu H, Shi Y Q, et al. On modeling MPEG video traffics. IEEE Trans. on Broadcasting, 2002, 48(4): 337–347.

12 Jiang M, Nikolic M, Hardy S, et al. Impact of self-similarity on wireless data network performance. IEEE ICC. IEEE. 2001. 477–481.

13 Przanowski K, Mamczarz J. Consumer finance data generator-a new approach to credit scoring technique comparison. General Information, 2012. arXiv: 1210.0057.

14 Liu JG, Lei H, Xue P, et al. Stability of similarity measurements for bipartite networks. Science Reports, 2016.

Simulate Generating Web Log Algorithm Using Fields’ Priority Relevance

QIU Zhi-Peng, XIAO Ru-Liang, ZHANG Rui

(Faculty of Software, Fujian Normal University, Fuzhou 350117, China) (Fujian Provincial Engineering Research Center of Public Service Big Data Analysis and Application, Fuzhou 350117, China)

The construction method of field relevance is a difficult problem in the Web data generation. A new algorithm for fields’ priority relevance based on maximal information coefficient is proposed. The algorithm is completely different from the existing method. Firstly, the maximal information coefficient between the appropriate fields needs to be extracted from real Web log data. Then, combined with the field of heavy tailed characteristics, the field is modeled by stretched exponential distribution. Finally, real data’s field dependence is simulated by the fields’ relevance model, so as to generate a realistic target data set. The experiments show that the generated data sets can maintain a reasonable balance between the fields and the similarity between the nodes.

fields’ relevance; data generation; maximal information coefficient; heavy tail

福建省科技计划重大项目(2016H6007)

2016-07-04;

2016-08-08

[10.15888/j.cnki.csa.005662]