无控制点航空遥感图像几何校正算法应用

江 倩，盛启慧，李启明，刘毓博，高 军



无控制点航空遥感图像几何校正算法应用

江 倩1，盛启慧1，李启明1，刘毓博2，高 军1

（1. 上海海事大学，上海 201306；2. 中国科学院上海技术物理研究所，上海 200083）

航空遥感图像有着特殊的几何畸变特性以及现实中无法及时获取野外控制点的限制条件，无法使用传统的几何校正方法对图像进行处理。针对航空遥感图像的限制条件，本文使用了无地面控制点的航空遥感图像几何校正模型对图像进行处理。通过实验对比仿射变换模型和多项式变换模型的校正效果，得出仿射变换模型更能适用于本文情况，更能改善图像效果。在几何校正过程中，提出了一种控制点的最佳选取方案，实验结果表明，该方案可以有效配合图像几何校正的实施。

航空遥感图像；无地面控制点；几何校正

0 引言

近几年来，在传感器技术和计算机技术的迅猛发展背景下，航空遥感图像也广泛应用于多个领域，在我们生活中起着特别重要的作用。面阵摆扫型相机在这个发展过程中脱颖而出，主要是因为其在进行对地观测成像时，有着灵活机动、视场大、效率高以及倾斜成像等优势，而且面阵摆扫型传感器可以弥补传统面阵CCD或者面阵多拼相机在成像视场上的不足，其摆扫成像的方式能够快速获取大范围的地面目标。因此，各国投入了极大的人力和物力研制生产一些满足自身需要的面阵摆扫型传感器，特别是在航空侦查领域。随着面阵摆扫型传感器的迅速发展，如何对图像数据进行高质量且有效的几何校正成为研究热点[1]。常规的航空对地观测数据处理方法通常需要高精度的内外方位元素、较大的影像重叠和地面控制信息的参与，这些条件都是面阵摆扫型成像系统无法满足的。目前国内外对于面阵摆扫型成像系统的研究大多数都会集中在传感器硬件系统，在面阵摆扫型航空影像数据的一些处理方法极度匮乏。为了更好地应用该类型航空遥感，特别需要开展这一背景下的几何校正技术的研究，以便更好地进行图像的拼接工作。

在遥感图像几何校正领域已有的研究：

Bentoutou Y.等人[2]在2005年提出了一种新的卫星遥感图像配准方法，该技术使用的图像边缘最鲜明的区域作为控制点，该算法已成功应用于实践中。实验结果表明，该算法具有较好的鲁棒性，效率和准确性。周海芳等人[3]在2006年首先研究了基于多项式变换的几何校正算法，提出了一种新的并行几何校正算法，有效提高了图像预处理的效率。该算法通过局部边界计算来实现延迟通信，解决了局部性问题。

H Goncalves等人[4]在2009年研究了几何校正过程中图像配准方法的应用，文献中说明了自动图像配准没有广泛使用的原因是缺乏客观和自动化的图像配准过程质量分析的标准，同时文献提出了一些几何校正图像配准过程中的客观评价。曹玲玲等人[5]在2011年提出了一种遥感图像的快速几何校正算法，该算法把畸变的图像划分为多个子块，分别对子块进行重采样计算，在重采样计算上还使用了最大程度减少坐标变换的冗余计算方法。经过实验证明了此算法对遥感图像的处理速度有所提高。

李庆鹏等人[6]在2011年提出了利用少量地面控制点，采用基于严格仿射变换模型求解遥感影像的RPC参数，并对CBERS-02B卫星HR相机遥感影像进行了试验，获得出有意义的结论。王子维等人[7]在2015年，针对无人机在执行任务过程中通过数码相机来获得的低空遥感图像在进行拼接时所涉及到的一些关键技术进行研究，引入了多项式算法进行几何校正。

张姣等人[8]在2015年，提出了一种结合仿射变换和多层B样条配准的图像校正，来解决大气湍流引起的图像抖动和图像偏移问题，采用仿射变换描述目标整体运动，引入多分辨率策略处理像素偏移，利用多层B样条对湍流引起的局部形变进行刚性配准。结果表明：该方法能够有效降低湍流造成像素偏移畸变，在噪声和模拟干扰下校正结果仍然理想。

P Durand等人[9]在2015年应用了一种原始的方法来纠正雷达图像几何畸变，文献中使用的图像为SPOT卫星（地球观测卫星）采集图像，雷达图像是通过法国东南部的机载雷达传感器Varan获得的。该算法是通过数字地形图生成与雷达图像点的对应关系，完成校正。高精度几何校正一直是航空高光谱遥感图像处理过程中难度很大的问题，而常规的遥感图像处理方法（即通过选取地面控制点来校正图像的方法）无法适用在航空高光谱图像的校正中[10]。这是因为在地理环境复杂或数据实时性要求的限制下，不能实时获取实测的野外控制点。因此本文把有重叠部分的图像作为一组基准图像和待校正图像，通过采集重叠区域的同名点作为控制点来实现航空高光谱遥感图像的几何校正。本文主要比较了仿射变换模型和多项式变换模型的几何校正方法在此背景下的应用，在几何校正过程中，设计了一套特殊的控制点采集方案，达到了较好的校正效果并为之后的拼接打了坚实的基础。

1 航空遥感图像几何校正

相机系统自身的光学误差、系统集成的误差以及面阵摆扫式传感器多投影成像等特点，导致面阵摆扫航空影像的几何畸变模型是相当复杂的。几何校正作为图像拼接不可或缺的部分，校正的好坏直接影响着图像拼接的效果。为了高质量完成之后的拼接工作，本文将重点进行几何校正的研究。遥感图像几何校正算法主要有两个步骤：一是像素坐标变换；二是像素亮度的重采样[11]，主要流程如图1所示。

图1 航空遥感图像几何校正流程图

1.1 确定图像角色

传统几何校正主要是以已校正过的遥感图像为基准图像或者使用大量的地面控制点对待校正图像进行几何校正。但如今面临的问题是无法及时获取地面控制点，此时将使用无地面控制点的几何校正方法对图像进行校正。在同一个航带内，首选传感器下视点（摆扫角为0°）的遥感图像为基准图像，主要因为此处图像较其他位置图像有较小的几何畸变，在一定的情况下，这样的几何畸变可忽略。基准图像确定后，将以仿射方式对同一航带内的其他图像进行几何校正。

1.2 选取控制点

1.2.1 选取方案设计

根据几何畸变的原理得知，整个图像的中心点位置为几何畸形可能最小的区域，几何畸形的程度随着距离的扩散而变大，因此本文以距离中心点接近的图像作为基准图像，而远离中心点的图像作为待校正图像[12]。

首先将基准图像和待校正图像分别命名为1和2，如图2所示。在实验过程中得知，图像重叠区域的边缘处的控制点数影响着整个几何校正的效果，因此本文把重叠图像的重叠边缘处作为重点取控制点区域，也就是图2所示的12、34、14和23，为了准确构建整个重叠区域的控制点带，本文将重叠区域的对角线位置也列入重点取点区域，也就是图2中的13和24，除此之外的区域也需要取控制点，但不列入重点取点区域。在提取控制点的过程中，本文采取了一些必要的筛选和配对，保证所有提取的控制点对都是有效的。

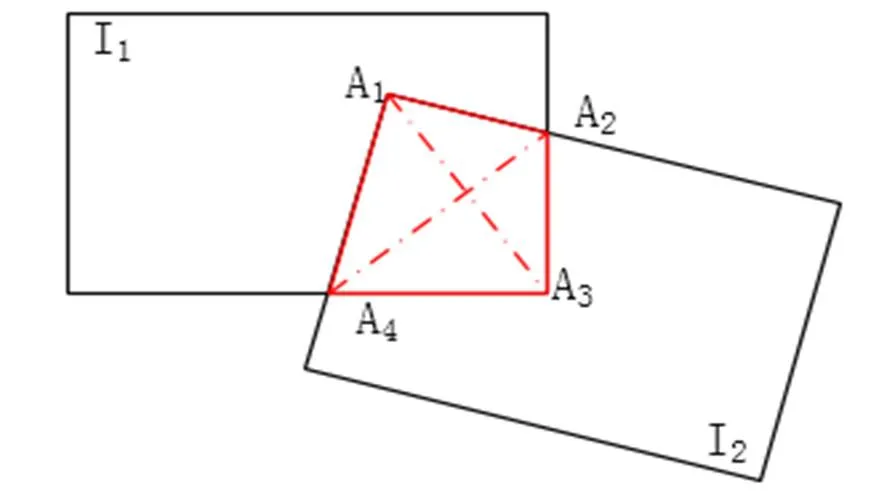
图2 控制点选取指示图

1.2.2 控制点的挑选

选择控制点是影响着多项式系数的求解误差大小的重要因素。通常选择控制点的方式是通过目测，选取目标性比较强的点作为控制点，比如建筑物的棱角、操场边缘或者河流等。但控制点的选取有一个标准，其精度的衡量尺度为RMS（Root Mean Square）参数，公式如下所示：

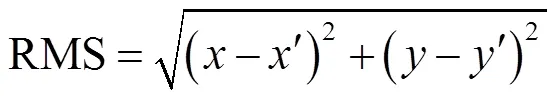
式中：,为无几何畸变的图像控制点坐标；¢,¢为变换后的图像控制点坐标，以图像像素大小为单位。控制点的RMS能够较好地挑选控制点，需要将RMS的值控制在1以内，几何校正才能达到较好效果。

1.3 几何校正模型

1.3.1 仿射变换模型

二维仿射变换（Affine Transform）可以用下式(2)来表示：

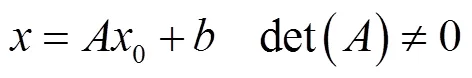
式中：,0,Ï2；∈2×2；是对0进行仿射变换的结果。当拍摄对象与摄像机之间的距离远远大于拍摄对象自身的大小时，仿射变换可以被近似为透视变换。平移、缩放、反射、旋转和错切是二维仿射变换的一些特殊情况，常用的二维仿射变换总是可以表示为这5种变换的组合[13]。

1.3.2 多项式变换模型

多项式变换模型通过一般多项式表示校正前后图像的对应点之间的坐标关系[14]，其可以用于从一个坐标系导出另一坐标系中的对应点的坐标：

式中：(,)是像素的校正坐标；(,)是校正前坐标；a、b是多项式系数。几何校正成功与否的关键是二元次多项式系数中和的解。当前求解方法的核心是通过存在于两幅图像上的若干个控制点的坐标，建立次多项式系数的方程组，进行求解，使用最小二乘法，获得二元次多项式的系数。

为了达到基准图像与待校正图像间坐标的完全配准，这时需要分析和尝试最佳的空间变换模拟式。在二元次多项式中，为了有效提高几何校正的精度，需要关注的重点主要可以分为两个方面:

一是多项式中值的确定，会直接影响到几何畸变的复杂程度，从理论上讲，值的增加，可以校正更加复杂的图像几何畸变，但计算量也会随之增加，综合这些实际情况，应用中的值通常取小于等于3。

二是控制点数目的确定，在应用多项式变换模型时，需要确定多项式的次方数，通常为2或3次。在选取控制点时，最少控制点个数与其直接相关，若多项式为次，其最少控制点个数为(＋1)(＋2)/2。但是，在实际应用中，使用最小数量的控制点，几何校正的效果通常不好。所以在条件允许的情况下，控制点的数量应远大于最小数量，可以是6倍或更多倍，以确保更好的几何校正效果。

1.4 图像重采样

经过几何变换，图像的坐标为无几何畸变坐标，每个像素分配的也是无几何畸变坐标，那么需要做的是分配每个无几何畸变像素亮度值。由于已知图像数据是具有几何畸变的像素亮度值，没有无几何畸变的像素亮度值，因此可以使用诸如最近邻法，双线性插值法和三次卷积插值法的数学重采样方法来计算校正后的像素的亮度值。在重采样方法中，虽然工作量相对较大，但是图像质量保存更好，性能的细节更清晰，是许多遥感软件的首选方法，因此本文将使用三次卷积插值法来进行重采样[15]。

1.5 图像拼接

通过图像的校正，得出了校正后图像。在选取控制点的过程中，已经建立了基准图像与校正图像特征点的一对一关系，通过这一关系可以实现图像间的配准，最终实现图像的拼接。图像拼接的目的是检验两种校正算法生成的图像与基准图像重合度。

如图3下半部分图像为校正后图像（图中校正图像使用的校正方法为仿射变换），上半部分图像为基准图像，重叠部分已在图片上显现出来。

2 实验结果及分析

本文所用数据为2016年2月上海技物所航拍横店影视城明清宫苑周边的遥感图像，选取进行对比实验的图像为岩前村的部分图像，本次采集数据是在天气晴朗的情况下，且采集目标为平坦的土地以及房屋等，辐射失真较小，可忽略不计。相机成像参数如表1所示。

图3 图像拼接重叠部分示意图

数据采集所使用的传感器为面阵摆扫式传感器，其不同于以往的传感器，是一种复杂的成像系统，主要有以下特点：

1）图像重叠率不完全一致，由于飞机在运行过程中抖动大且姿态不稳定，在机械摆扫过程中也存在着系统误差，使得同一航带内或者航带间影像序列的重叠率不一致。

表1 相机成像参数

2）多中心投影成像，当摆扫到下视点（摆扫角为0°）时，属于中心投影成像，当摆扫角成一定角度时，属于倾斜中心投影成像，如图4所示。

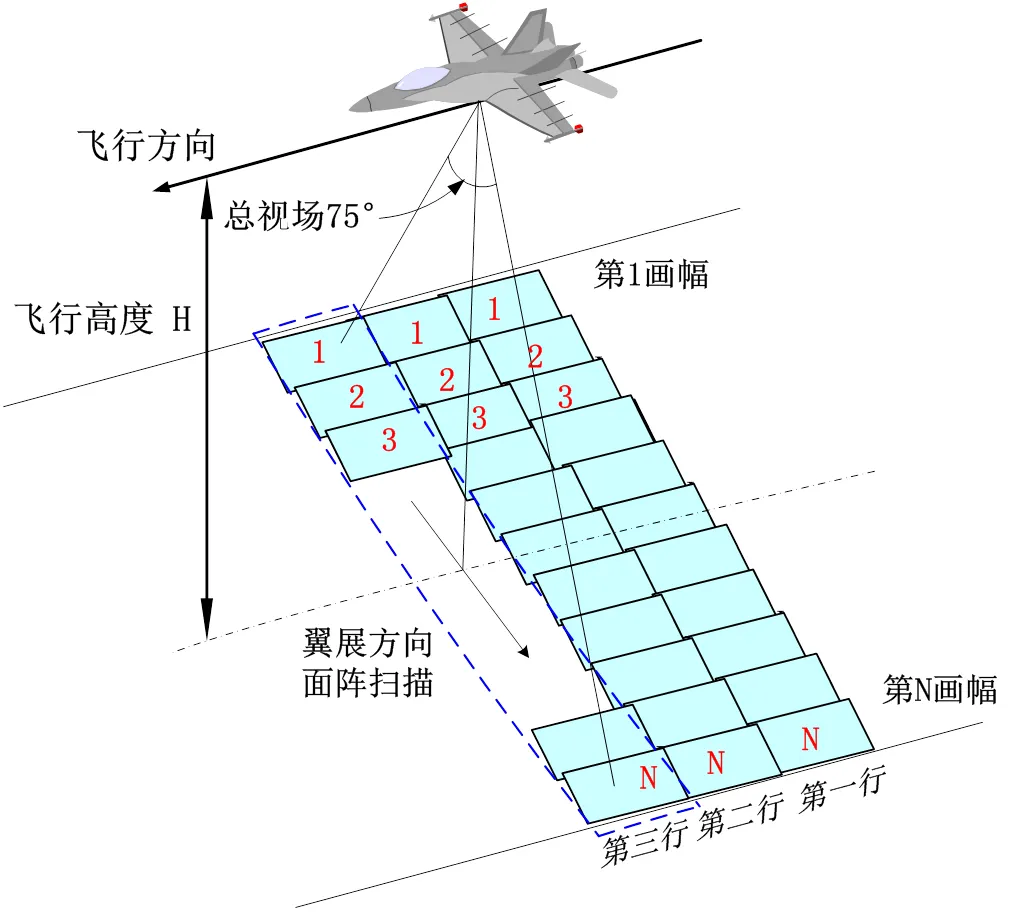
图4 面阵扫描宽幅成像原理

根据面阵摆扫传感器的特性，可得出该传感器得到的航空遥感图像的几何畸变形成的原因有如下几点：

1）传感器内方位元素精度无法保证，内方位元素是用来恢复摄影时光束形状，能够确定摄影中心与图像的相对位置关系，在实验过程中应进行严格的校验，得到高精度的内方位元素来确保后续实验的有序进行；

2）光学畸变，通常是以正片和负片的形式出现在镜头上；

3）由于摆扫式传感器的多中心投影成像方式，很容易形成一种全景效应。即当飞行高度和总视场一定的情况下，传感器在摆扫角最大的情况下成像的有效像元比下视点（摆扫角为0°）时要大；

4）姿态位置误差，这是由于传感器的轴线偏离重力作用方向而引起的一种误差，这种误差会直接导致图像的几何畸变。

本文设计了独特的控制点采集方案对图像控制点进行采集，使用了两种几何校正算法对图像进行几何校正。根据以往的经验以及优劣对比，本文采取三次卷积内插的重采样方法进行实验，在实验过程中验证了控制点采集方案的有效性以及更加适用于本文的情境的几何校正算法。

2.1 图像校正结果及分析

图5中一共有3张图像，(a)是待校正图像，(b)是通过仿射变换模型以及3次卷积内插的重采样方法进行几何校正得到的图像，(c)是通过多项式变换模型以及3次卷积内插的重采样方法进行几何校正得到的图像。

由于仿射变换为线性变换，多项式变换为非线性变换，线性变换是通过适当的平移、旋转、缩放和反转（镜像）来实现变换，这样一幅图像中的直线经过变换映射到另一幅图像，仍然保持着平行关系，这样的变换能够较大程度上保持着图像原来的形态，不会产生二次畸变。从对比中可以看出，通过仿射变换模型校正的图像与原图像相比没有较大的形态改变，但是多项式变换模型校正后生成的图像在形态上有了较大改变、物体间距变大且图像面积比例变化较大，使得图像效果有所改变，因此仿射变换模型还是比较令人满意且适用于本文情况的。

2.2 拼接重合度结果及分析

图6是通过仿射变换模型和多项式变换模型进行几何校正后的图像分别与基准图像进行配准得到的拼接结果。从图6可以看出，多项式变换模型校正后的图像物体各点间的间隔变大且没有较好保持原有图像的状态，使得图像有一种被放大的感觉，这将会影响到后续图像的拼接效果进而产生拼接的积累误差，而使用仿射变换模型校正的图像经过拼接后整体效果较好，在一定程度上其优于使用多项式变换模型校正的图像。

图5 仿射变换模型和多项式变换模型几何校正结果

Fig.5 Affine transformation model and polynomial transformation model

图6 仿射变换模型和多项式变换模型校正后拼接结果

2.3 控制点对实验结果的影响

从图7(a)和(b)中可以看出，控制点采集是按照文中设计的采集方案进行的，将控制点采集范围控制在重叠区域，尤其是对重叠边缘的采集，主要选择具有明显特点或者棱角的建筑物、交叉路口等作为控制点。

图8(a)为利用传统方法来采取图像的控制点信息，通过仿射变换的几何校正模型进行校正，将校正后图像与基准图像进行拼接重合度实验得到的图像。图8(b)为利用本文方法来采取图像的控制点信息，通过仿射变换的几何校正模型进行校正，将校正后图像与基准图像进行拼接重合度实验得到的图像。经过对比可知，传统方案在临界处两张图像无法完全配准，使重叠部分无法完美重合，拼接的图像有明显的拼接误差，而利用本文控制点选取方案得到的拼接图像，由于选取的控制点在图像配准处理过程中发挥了重要作用，使得呈现的拼接图像较为自然，无明显拼接缝隙。

图9是通过仿射变换模型校正后的8张图像经过对称式拼接的方法进行拼接的结果图，对称式拼接就是使得每次拼接缝隙的上下或者左右的图像个数是相同的，以此将图像校正的失误率控制到最低。在图像的拼接过程中，也会有积累误差影响着图像的拼接结果，例如前两张图像拼接时产生的误差若再继续进行拼接将会产生积累误差。为了减少积累误差，应使用适合实验样本的校正方法。

图7 控制点采集结果图

Fig.7 Control point acquisition results

图8 控制点采集对图像拼接的影像比较

Fig.8 Comparison of image mosaic with control point collection

图9 图像拼接结果

3 总结

本文主要是研究适用于航拍遥感图像进行几何校正的方法，首先考虑到无地面控制点的限制条件，本文使用无控制点的几何校正方法，同时提出了一种提取控制点的采集方案，通过这种方案提取的控制点校正图像使得图像较原图有了大幅度的改善，说明了该方案的有效性。通过两种几何校正模型的比较实验，得出仿射变换模型进行校正的图像效果更佳，适用于本文情况，可以进行批量校正。最后，文中将利用本文方法校正后拼接的图像展示出来，图像形态较好，但下一步还需要进行匀色处理，使得图像的观感效果更佳。

[1] 宋耀鑫. 面阵摆扫式航空影像几何校正与无缝拼接技术研究[D]. 北京: 中国科学院大学, 2014.

Song Yaoxin. Study on the Geometric Correction and Seamless Stitching of Array Whiskbroom ScannerAerial Image[D]. Beijing:Chinese Academy of Sciences,2014.

[2] Bentoutou Y, Taleb N, Kpalma K, et al. An Automatic Image Registration for Applications in Remote Sensing[J]., 2005, 43(9): 2127-2137.

[3] 周海芳, 易会战, 杨学军. 基于多项式变换的遥感图像几何校正并行算法的研究与实现[J]. 计算机工程与科学, 2006, 28(3): 58-60.

Zhou Haifang, Yi Zhan Zhan, Yang Xuejun.Investigation and Realization of Parallel Algorithms for the Geometric Correction of Remote Sensing Images Based on Polynomial Transform[J]., 2006, 28(3):58-60.

[4] Goncalves H, Goncalves J A, Corte-Real L. Measures for an Objective Evaluation of the Geometric Correction Process Quality[J]., 2009, 6(2): 292-296.

[5] 曹玲玲, 张永梅. 基于多项式的遥感图像快速几何校正[J]. 电脑开发与应用, 2011, 24(1): 5-7.

Cao Lingling, Zhang Yongmei.The Rapid Geometric Correction of Remote Sensing Images based on Polynomial Transform[J]., 2011, 24(1): 5-7.

[6] 李庆鹏, 王志刚, 陈琦. 基于严格仿射变换模型的遥感影像RPC参数求解[J]. 测绘地理信息, 2011, 36(3): 1-4.

Li Qingpeng, Wang Zhigang, Chen Qi. RPC Parameters Calculation of Remote Sensing Imagery Based on Strictly Affine Transformation Model[J]., 2011, 36(3): 1-4.

[7] 王子维. 无人机遥感图像的拼接技术研究[D]. 大庆: 东北石油大学, 2015.

Wang Ziwei. Research on Mosaic Technology Based on UAV Remote Sensing Image[D]. Daqing: Northeast Petroleum University, 2015

[8] 张姣, 李俊山, 杨亚威. 结合仿射变换和多层B样条配准的湍流畸变图像校正[J]. 光学精密工程, 2015, 23(3): 846-854.

Zhang Jiao, Li Junshan, Yang Yawei. Turbulence Distorted Image Correction Using Affine Transformation and Multilevel B-spline Registration[J]., 2015, 23(3): 846-854.

[9] Durand P, Luan J, Ghorbanzadeh D.[M]. Transactions on Engineering Technologies. Springer Netherlands, 2015: 657-668.

[10] 周小虎, 万余庆. IMU在航空高光谱遥感图像几何校正中的应用[C]//全国遥感技术学术交流会. 2003.

Zhou Xiaohu, Wan Yuqing. Application of IMU to the Georeferencing of Aerial Hyperspectral Remote Sensing Images[C]//, 2003.

[11] 曾丽萍. 遥感图像几何校正算法研究[D]. 成都: 电子科技大学, 2008.

Zeng Liping. Research on Remote Sensing Image Geometric Correction Algorithm[D]. Chengdu: University of Electronic Science and technology of China, 2008.

[12] 刘异, 李玉霞, 童玲. 无地面控制点的无人机遥感影像几何校正算法[J]. 测绘通报, 2012(7): 57-59.

Liu Yi, Li Yuxia, Tong Ling. Geometric Correction for Unmanned Aerial Vehicle Remote Sensing Image without Ground Control Points[J]., 2012(7): 57-59.

[13] 李海彦. 基于仿射变换的多姿态人脸矫正与识别[D].苏州: 苏州大学, 2013.

Li Haiyan. Multi-pose Face Correction and Recognition Based on Affine Transformation[D]. Suzhou: Soochow University, 2013.

[14] 张建, 何宏昌. 资源一号02C影像的几何校正精度分析——基于RPC模型和多项式模型[J]. 池州学院学报, 2014(3): 65-67.

Zhang Jian, He Hongchang. Analysis of Geometric Correction Accuracy of Resource one 02C Image Based on RPC Model and Polynomial Model[J]., 2014(3): 65-67.

[15] 陈灿. 几何校正中重采样方法研究[D]. 成都: 电子科技大学, 2012

Chen Can. Severals Correct Medium Resampling Method Research[D]. Chengdu: University of Electronic Science and technology of China, 2012.

Application of Geometric Correction Algorithm for Aerial Remote Sensing Image without Control Point

JIANG Qian1，SHENG Qihui1，LI Qiming1，LIU Yubo2，GAO Jun1

(1.,201306,; 2.,200083,)

With the development of sensor technology, aerial remote sensing images are widely used in various fields, but the aerial remote sensing image has special geometric distortion characteristics and the field control point cannot be accessed timely in practice. So the traditional geometric correction method for image processing cannot be used. In this paper, the geometric correction model of aerial remote sensing image without ground control point was used to deal with the aerial remote sensing image. Compared with the affine transformation model and the polynomial transformation model, the affine transformation model is more suitable for the situation in this paper, and can improve the effect of image. In the geometric correction process, a control point selection scheme was proposed. Experimental results show that the proposed method can effectively coordinate the implementation of image geometric correction.

aerial remote sensing image，groundless control point，geometric correction

TP751

A

1001-8891(2017)05-0444-07

2016-12-27；

2017-04-18。

江倩（1996-），女，安徽桐城人，本科生，主要从事遥感图像处理研究。

高军（1979-），男，浙江嘉兴人，副教授，博士，主要从事图像处理、人工智能方面的研究，E-mail：jungao@shmtu.edu.cn。

上海市自然科学基金（14ZR1419700）。