多约束的运动模糊图像盲复原方法

卢 晶，胡 钢，秦新强



多约束的运动模糊图像盲复原方法

卢 晶1，胡 钢2，秦新强2

（1.商洛学院 数学与计算机应用学院，陕西 商洛 726000；2. 西安理工大学 理学院，陕西 西安 710054）

运动模糊图像的盲复原一直以来都是一个极具挑战的问题。为了能够准确地估计出运动模糊核（Motion Blur Kernel：MBK），进而得到高质量的复原图像，提出了一种基于正则化技术的多约束运动模糊图像盲复原方法。首先，为了能够准确地提取出图像中的大尺度边缘，提出了一种基于梯度选择的稀疏图像平滑方法；然后，在MBK的估计阶段，根据运动模糊核的内在特性，提出了一种多约束的正则化模型，同时结合提取的大尺度图像边缘，实现了对MBK的准确估计；最后，采用了半二次性的变量分裂策略对在模糊核估计阶段所提出的多约束正则化模型进行最优化求解，能够在准确估计MBK的同时得到高质量的复原图像。分别在人造的模糊图像和真实的模糊图像上进行了大量的实验，实验结果表明：提出的方法较近几年的一些代表性的较为成功的运动模糊图像盲复原方法相比，在主观的视觉效果和客观评价指标两方面都具有明显的改进。

运动模糊图像；盲复原；大尺度图像边缘；运动模糊核；多约束正则化模型

0 引言

在成像过程中，因为成像系统的偏差、散焦、大气湍流、噪声以及成像镜头与成像物体的相对位移等众多因素的影响，不可避免地会造成成像的模糊，质量的下降[1]。如今，随着便携式高像素成像设备和高清监控设备的普及，在引起图像质量退化的众多因素中，由成像设备与被拍摄物体之间的相对运动而造成的图像运动模糊已成为导致图像质量下降最主要的因素之一。因此，本论文主要针对运动模糊图像的盲复原方法进行研究。

运动模糊图像的盲复原就是在MBK（Motion Blur Kernel：运动模糊核）未知的情况下，仅由观察到的运动模糊图像复原出原始的清晰图像，并准确估计出MBK。BK（模糊核：Blur Kernel）是造成图像模糊的原因，错误的BK不仅不能够复原出原始的清晰图像，反而会进一步恶化图像的质量，因此能否准确估计出引起图像模糊的BK是模糊图像盲复原方法成功的关键。2006年，Fergus等人利用自然图像梯度的统计特性成功实现了真实运动模糊图像的盲复原[2]。该方法对复原图像进行了自然图像梯度的统计特性正则化约束，而针对MBK则运用了一种混合的指数分布来对其进行稀疏性的约束。2008年，Shan等人提出了一种分段函数来近似自然图像梯度的分布，对MBK则采用了单一的L1范数来对其进行稀疏性约束[3]。2009年，Cho等人提出仅利用图像中的强边缘会有利于MBK的估计，并提出了一种基于双边滤波器、shock滤波器和梯度阈值法的图像强壮边缘提取方法[4]。2011年，Krishnan等人提出了一种L1/L2的图像正则化约束项，但是对MBK对运动模糊核也仅是采用了单一的L1范数来对其进行稀疏性约束[5]。2012年，Cai等人提出了两种正则化约束项来同时对运动模糊核的稀疏性和连续平滑特性进行正则化约束：小波域的L1范数保证支持域的稀疏特性，运动模糊核像素值强度的L2范数保证支持域的连续性[6]。2013年，Xu等人提出了一种基于L0范数的稀疏表示方法的模糊图像盲复原方法[7]。2014年，Oliveira等人基于模糊图像的频谱，提出了一种运动模糊图像的盲复原方法[8]。但是该方法只能适用于简单的匀速直线运动模糊图像。为了在保护图像边缘的同时能够有效复原出图像的纹理细节，唐述等人于2014年提出了一种结合局部全变差模型和非局部全变差模型的图像复原模型，分别对图像的边缘和纹理细节进行正则化约束[9]。2014年，徐焕宇等人针对图像非局部梯度信息和图像块稀疏表示各自的优缺点，提出了一种稀疏表示与非局部全变差相结合的图像复原模型[10]。2015年，Ma等人提出了一簇分段的线性惩罚函数，对图像的梯度进行稀疏性约束[11]。2016年，Pan等人将L0范数分别运用到了复原图像的图像域和梯度域中，并对MBK进行了L2范数的稀疏性约束[12]。2016年，Schmidt等人将学习的方法运用到模糊图像的复原处理中，提出了一种递归的级联树域方法来实现模糊图像的复原[13]。

通过对现有的一些具有代表性的，且较为成功的运动模糊图像盲复原方法的分析可知，现有的方法几乎都存在一个主要的缺点：在MBK的估计阶段，现有的绝大多数方法仅考虑了MBK的稀疏特性，而忽略了MBK的连续平滑特性[2-5,7-13]。虽然有少量的方法同时考虑了MBK的稀疏特性和连续的平滑特性[6]，但实际上它们却并没有将MBK的稀疏特性和连续平滑特性真正完全的表现出来，因为在图像域进行L2范数的约束会使得求得的解更加偏向于稀疏而非连续平滑，因此文献[6]的方法从某种程度上来说也只是仅对MBK进行了稀疏性的约束。由此可见，现有的方法并不能将MBK的内在特性完全、准确地表现出来，并不能够真正准确地估计出MBK，从而不能得到高质量的复原图像。

针对现有方法存在的缺陷，本论文提出了一种新的多约束正则化运动模糊图像盲复原方法。提出方法的创新点主要有两方面：①本论文首先提出了一种梯度选择的稀疏图像平滑方法来准确提取出图像中的大尺度边缘；②在MBK的估计阶段，针对MBK的内在特性，提出了一种新的多约束的正则化模型来同时对MBK的稀疏性和连续平滑特性进行更好地约束，能够在满足MBK稀疏性的同时，更好地保证其连续平滑特性，实现MBK的真正准确估计。为了验证本论文提出方法的有效性，分别在人造的模糊图像和真实的模糊图像上进行了大量的实验，实验结果表明：提出的方法较近几年的一些代表性的且较为成功的运动模糊图像盲复原方法相比，在主观的视觉效果和客观评价指标两方面都具有明显的提升。

1 提出的多约束运动模糊图像盲复原方法

1.1 图像中大尺度边缘的提取和锐化

如前所述，在模糊图像中，仅当图像中边缘的尺度大于BK的尺度时，该图像边缘才能够有利于BK的估计。因此，图像中的大尺度边缘是相对于BK的尺度而言的，只要图像中尺度大于BK尺度的图像边缘就称为大尺度的图像边缘，反之，剩下的就是小尺度的图像边缘和噪声。基于该思想，本论文提出了一种基于梯度选择的稀疏图像平滑方法来准确提取出图像中的大尺度边缘，提出方法的数学模型如公式(1)所示：

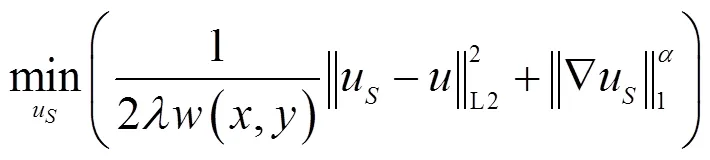
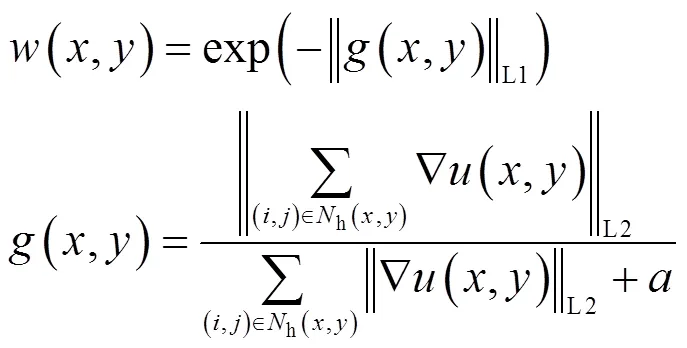
再分析公式(1)，加入了权重(,)的公式(1)实际上就是一种各向异性扩散的图像平滑操作。根据刚才对公式(2)的分析可知，较小的(,)值会导致(,)较大，从而能够较好地平滑掉图像中的小尺度边缘、噪声和平滑区域；相反，较大的(,)值则保证了图像中的大尺度边缘所受到的平滑影响较小。因此，很容易想到：只要将图像块h(,)的大小设置为等于或者略大于MBK的支持域，那么，在LSIEES阶段，本论文所提出的基于梯度选择的稀疏图像平滑方法（公式(1)和公式(2)）就能够很好地平滑掉图像中的小尺度边缘和噪声，将图像中尺度大于MBK尺度的大尺度边缘准确地提取出来。

在大尺度边缘被提取出来之后，还将对其进行初步锐化的预处理，在这里，本论文采用了现有方法中常用的shock滤波器[7]来对提取的大尺度图像边缘进行初步的锐化处理。

1.2 MBK的准确估计

如果将MBK转化成一幅图像，那么它反映的是成像设备与被拍摄物体之间相对运动的轨迹，是一条很“细”的且连续平滑的“曲线”，因此MBK应同时具有支持域的稀疏特性和连续的平滑特性[6]。针对MBK的这些内在特性，在Cai等人方法[6]的启发下，本论文提出了一种新的多约束的正则化模型来同时对MBK的稀疏性和连续平滑特性进行更好地约束，其数学模型为：

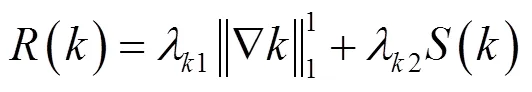
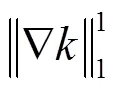
由以上的分析可知，本论文提出的针对MBK的多约束的正则化模型（公式(3)），能够在满足MBK稀疏性的同时，更好地保证其连续平滑特性，将MBK的内在特性完全充分的表现出来，因而能够估计出更加准确的MBK。结合LSIEES阶段所得到的shock滤波之后的大尺度图像边缘，本论文提出的MBK估计的数学模型为：

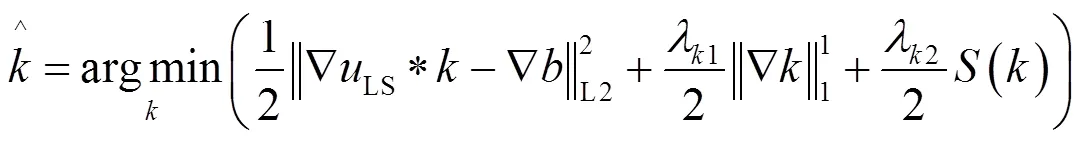
式中：LS是在LSIEES阶段得到的锐化的大尺度边缘图像；表示观察到的运动模糊图像。需要注意，在LSIEES阶段，公式(1)的目的是提取出图像中的大尺度边缘，因此最理想的解是S仅具有大尺度的图像边缘，图像中的小尺度边缘和噪声都被完全的平滑掉。显而易见，一幅仅含有大尺度边缘的图像的梯度会比没有平滑的原始图像的梯度更加稀疏，因此本论中，的取值为0.5。

1.3 图像的复原

利用在MBKE阶段得到的MBK，在图像的复原阶段，本论文采用了文献[14]的非盲复原方法来对模糊图像进行复原，其数学表达式为：

式中：表示待求解的复原图像；为图像的正则化参数。

2 对提出方法的求解

本小节仅主要介绍对公式(4)的求解，因为对公式(1)的求解可采用同样的方法，因此这里就不再赘述。针对提出的多约束正则化模型（公式(4)），本小节将采用半二次性的变量分裂策略对其进行求解，因此公式(4)可等效为：

因此，首先引入一个新的变量1，并产生一个约束项：1＝Ñ，那么提出的模型（公式(4)）便转化成一个新的非约束最优化问题：

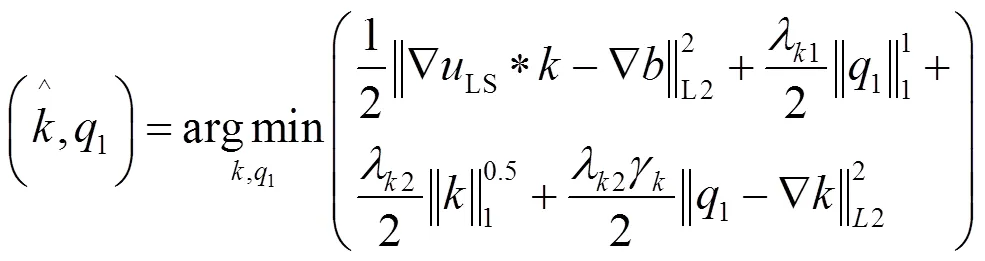
接下来，利用交互式的迭代策略对公式(7)进行求解：

①固定1，求解，对应的代价函数为：

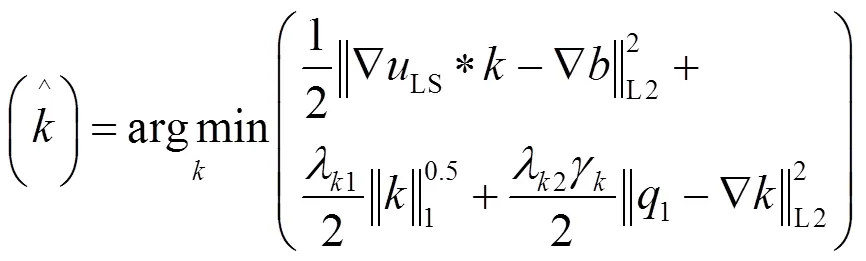
很明显，这是一个二次性的函数，因此，直接对求导，并利用快速的傅里叶变换可得到：

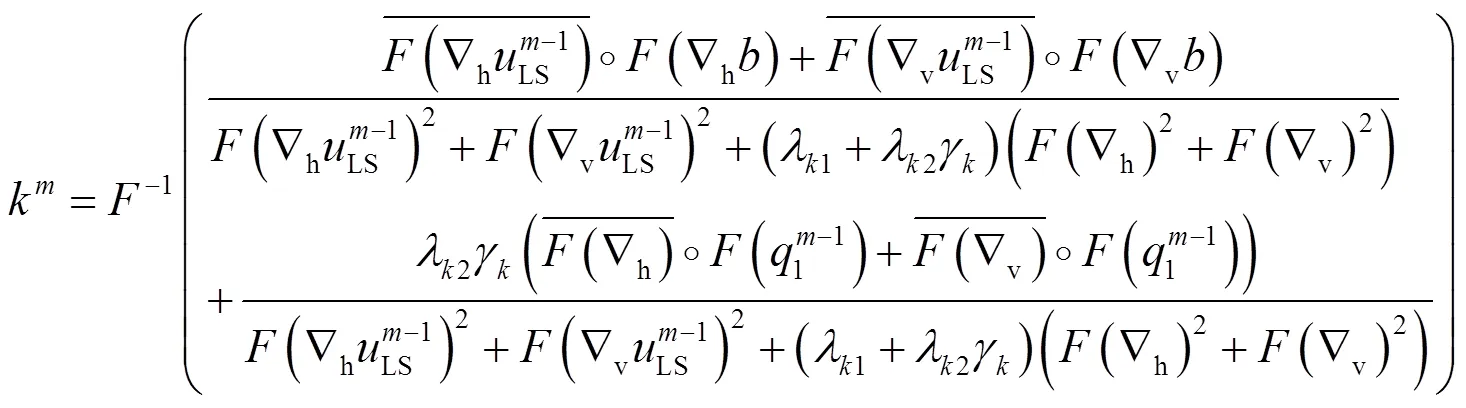
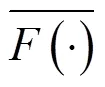
为了得到具有物理意义的解，在每一次迭代中，采用了盲复原方法中通用的一类约束条件对估计的MBK进行约束：

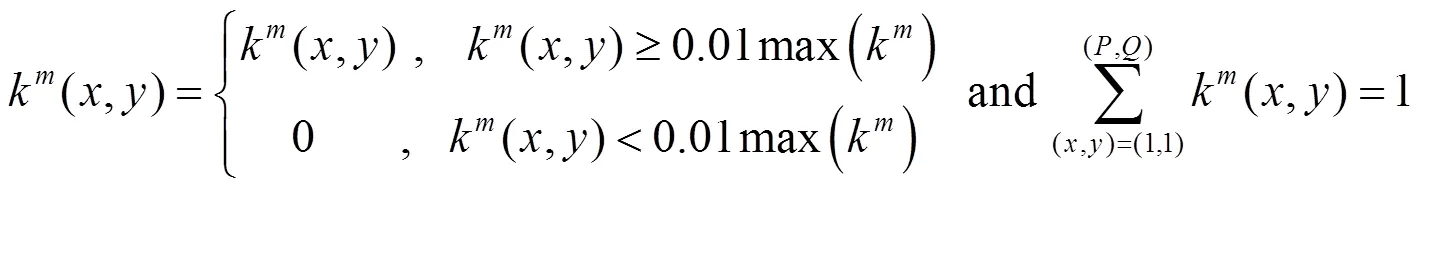
式中：max(k)表示k中最大的元素；×为MBK的大小。

②固定，求解1，对应的代价函数为：

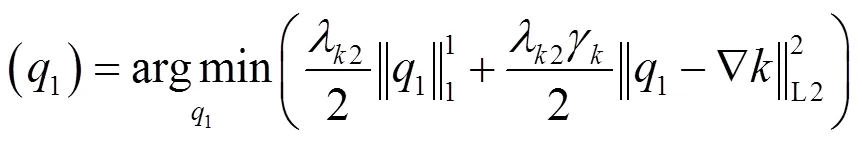
对公式(11)，采用文献[14]中的方法，得到：

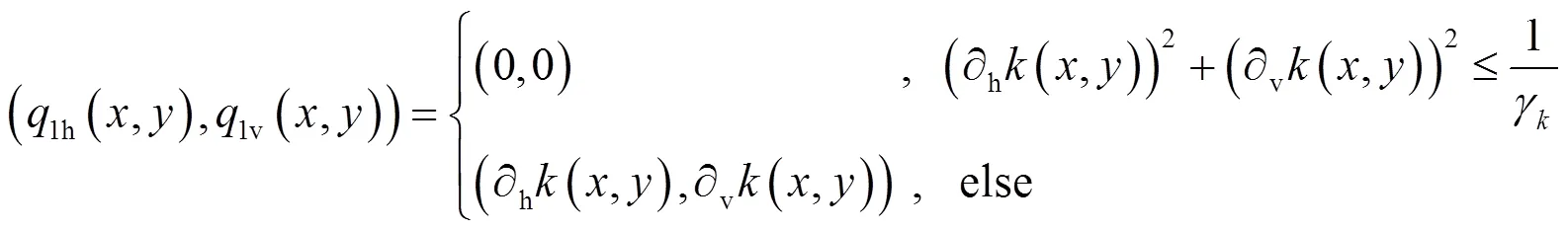
对于图像的复原（公式(5)），因为本论文是完全采用了文献[14]的方法，因此，只要将公式(9)中求得的直接代入到公式(5)中，然后直接运用文献[14]中的方法对其进行求解即可，这里也不再赘述，有兴趣的读者可参考文献[14]。

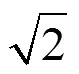
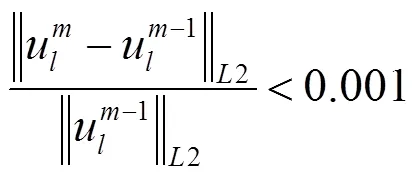
式中：u表示在第层第次迭代的复原图像结果。在算法的初始阶段，变量1的初始值为0。

3 实验结果及分析

本论文将提出的方法与近几年提出的一些极具代表性的且较为成功的运动模糊图像盲复原方法进行了比较（文献[6]，文献[7]和文献[11]）。在客观的评价指标方面，本论文采用了PSNR（Peak-Signal -Noise-Ratio：峰值信噪比），定义为：

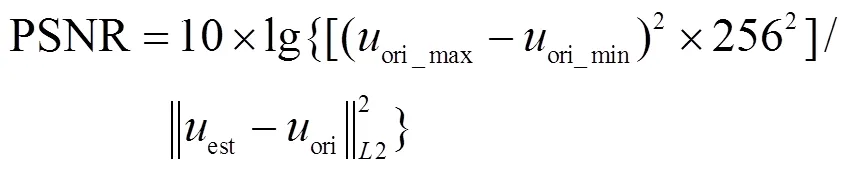
来客观比较本论文实验中所涉及到的方法的性能，其中ori为原始的清晰图像；est为复原图像；ori-max和ori-min分别表示为ori中元素的最大值和最小值。本论文实验所涉及到的方法均是在Windows7的操作系统上运行的，实验所用的计算机具有8G内存和2.3GHz的双核Intel处理器。为了保证实验的公平性，实验中的所有实验结果都是经过了大量的实验，通过对每种方法中参数的反复调试，而得到的最佳复原结果。

3.1 提出方法中的参数设置

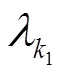
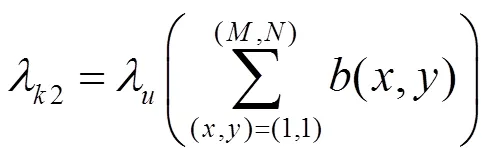
式中：×表示模糊图像的大小。参数控制着变量1与Ñ之间的相似程度，本论文采用了一种连续的增加策略，即在算法的初始阶段对参数设定一个较小的初始值，然后在每次迭代之后对的值加倍，也即是：＝1.5－1，直到达到的最大值为止。在本论文的实验中，的初始值0＝1.5，最大值max＝2×106。

3.2 人造运动模糊图像的实验

在人造的运动模糊图像的实验中，本论文采用了文献[7]中所采用的图像数据：4幅255×255大小的灰度级标准测试图像（如图1所示）和文献[7]中所采用的5种不同类型的运动模糊核（如图2所示）验证本论文提出方法的性能。图1所示为本论文实验中所使用的4幅255×255大小的灰度级标准测试图像。图2所示为实验中所使用的5种不同的运动模糊核。实验中，所有的模糊图像均被加入了BSNR＝35dB的加性高斯白噪声。

图1 实验中所采用的4幅灰度级测试图像

由图1和图2可知，该图像数据库总共可产生出20幅人造的运动模糊图像。本论文对所有的20幅人造运动模糊图像均进行了比较实验，但是因为篇幅的原因，在主观的视觉比较方面，这里只给出了其中一幅图像结果的主观视觉效果比较图，如图3所示。图3(a)所示为利用测试图像“Face”和MBK5所得到的人造运动模糊图像。

图2 实验中所采用的5种不同类型的运动模糊核

如图3(b)所示，虽然Cai等人的方法[6]同时考虑了运动模糊核的稀疏性和连续平滑特性，但是如前所述，该方法实际上还是偏向于稀疏性，因此该方法所估计的MBK仍然会出现间断，从而导致该方法并不能复原出准确的图像。Xu等人的方法[7]所估计的MBK会产生出类似于振铃的瑕疵，并且，该方法所得到的复原图像呈现出分段常数的块状瑕疵（图3(c)）。Ma等人的方法[11]所估计的MBK过于集中，并且得到的复原图像整体较暗（图3(d)）。相比之下，因为本论文提出的多正则化约束能够对MBK的稀疏特性和连续平滑特性进行更好的约束，因此本论文提出方法所估计的MBK最接近真实的MBK，同时能够获得最清晰锐化的高质量复原图像（图3(e)）。图3证明了，在人造的运动模糊图像中，本论文提出的方法能够得到最好的主观视觉效果。

接下来，本章节将利用PSNR来客观评价所提出方法的性能。如表1所示，从客观的PSNR这个评价指标方面将本章提出的方法与Cai等人的方法[6]、Xu等人的方法[7]和Ma等人的方法[11]进行了比较。

由表1可以很明显的看到，本论文提出的方法明显优于另外3种运动模糊图像盲复原方法，在所有的20幅人造模糊图像的实验中总是能够获得最高的PSNR值。表1从客观的评价指标方面证明了本论文提出方法的性能。

3.3 真实运动模糊图像的实验

为了进一步验证本论文提出方法的性能，接下来，将提出的方法运用到真实运动模糊图像的盲复原中。

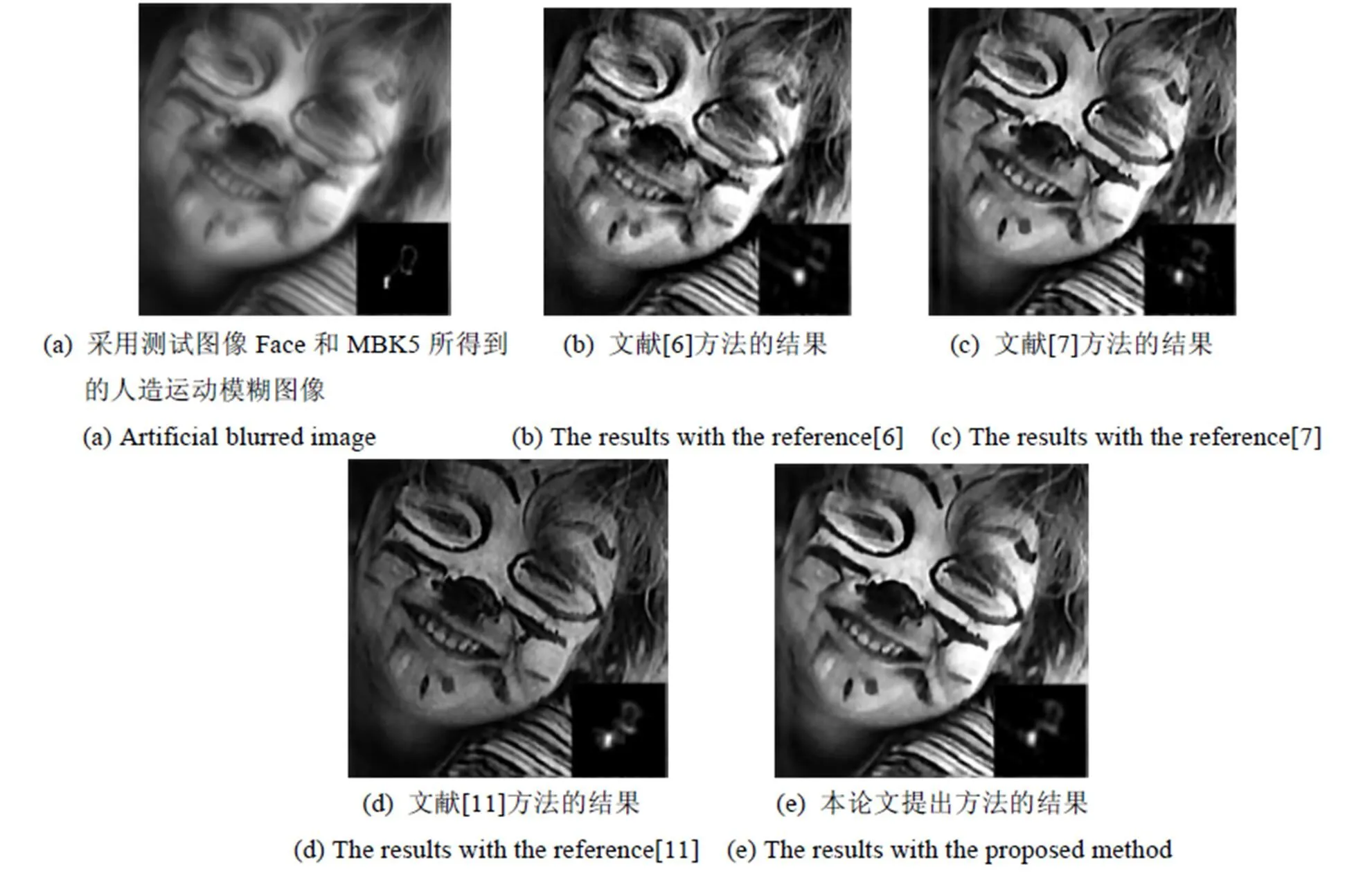
图3 所有方法在测试图像Face和MBK5上的实验结果

图4(a)为文献[7]中的一幅真实运动模糊图像，其大小为593×417，在实验中，我们假定MBK的大小是已知的，对于图4(a)，MBK的大小被设定为63×63个像素。如图4(b)所示，与人造的模糊图像类似，Cai等人的方法[6]所估计的MBK的支持域并不连续，有明显的间断，对应的复原图像也出现了较多的噪声干扰和振铃瑕疵。Xu等人的方法[7]所估计的MBK同样具有类似的间断（图4(c)）。与Cai等人和Xu等人的方法相比，Ma等人的方法[11]能够估计更合理的MBK，但是其模糊图像中却出现了类似于鬼影的瑕疵（图4(d)）。相比之下，本论文提出的方法不仅能够估计出更准确的MBK，而且对于复原图像而言，还能够有效抑制其他方法中存在的瑕疵，复原出最高质量的复原图像（图4(e)）。

图5(a)为另一幅极具代表性的真实运动模糊图像，其大小为454×588，其MBK的大小为35×35个像素点。需要注意，该幅图像中还包含有许多的小尺度的图像纹理细节（例如大量的树叶），因此对该幅图像是一幅比较有挑战性的真实运动模糊图像。如图5所示，Cai等人的方法[6]、Xu等人的方法[7]和Ma等人的方法[11]的复原结果或多或少都含有一定的瑕疵。Cai等人的方法[6]所估计的MBK同样具有间断的现象（图5(b)）。虽然Xu等人的方法[7]所估计的MBK没有间断，但是却出现了分支；在复原图像方面，虽然够复原出较多的图像细节，但同时也产生出了严重的振铃瑕疵（图5(c)）。Ma等人的方法[11]会产生出过度平滑的复原图像，该类复原图像中的大部分边缘和纹理细节已被平滑掉（图5(d)）。相比之下，本论文提出的方法估计出了最准确的MBK，没有间断，没有分支；在图像复原方面，本论文提出的方法能够在复原出更多的图像细节的同时有效抑制其他方法中出现的振铃瑕疵（图5(e)）。

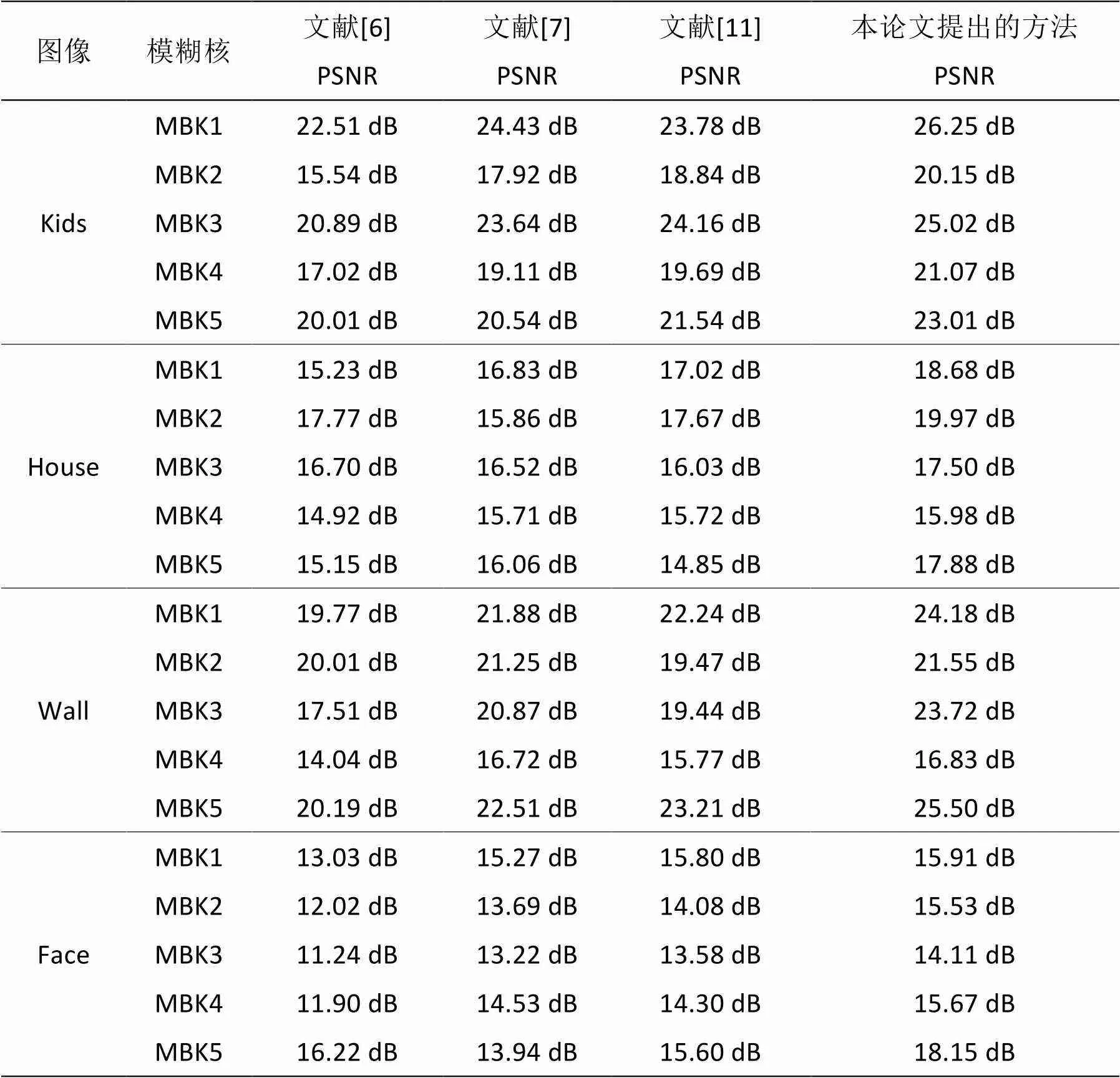
表1 文献[6]中方法，文献[7]中方法，文献[11]中方法和本论文提出的方法在所有20幅人造模糊图像盲复原的实验中所得到的PSNR (dB)值

图4 真实运动模糊图像的盲复原结果、估计的运动模糊核和对应图像的局部放大图

图5 真实运动模糊图像的盲复原结果、估计的运动模糊核和对应图像的局部放大图

4 结论

本论文主要针对运动模糊图像的盲复原问题进行了研究，主要创新工作集中在MBK的准确估计方面。为了能够准确地估计出MBK，本论文首先，提出了一种基于梯度选择的稀疏图像平滑方法来准确提取图像中的大尺度边缘；然后，在MBK的估计阶段，针对现有方法中普遍存在的缺点，进步一对稀疏性和连续平滑特性进行了分析，提出了一种能够对MBK的稀疏性和连续平滑特性进行更好约束的多约束正则化模型（梯度域的L2范数约束连续平滑特性，梯度域的L0范数约束稀疏性），能够在满足MBK稀疏性的同时，更好地保证其连续平滑特性，实现MBK的真正准确估计。最后，采用了半二次性的变量分裂策略对提出的模型进行最优化求解。在实验部分，分别在人造的模糊图像和真实的模糊图像上进行了大量的实验，实验结果表明：提出的方法较近几年的一些代表性的较为成功的运动模糊图像盲复原方法相比，在主观的视觉效果和客观评价指标两方面都具有明显的改进。

将提出的方法运用到实际生活中存在的空间变化的，以及非线性等更加复杂的模糊图像盲复原中，是接下来研究工作的重点。

[1] GONZALEZ R C, Woods R E. 数字图像处理[M]. 阮秋琦, 阮宇智译. 3版: 北京: 电子工业出版社, 2011.

GONZALEZ R C, Woods R E.[M]. Translated by Qiuqi Ruan, Yuzhi Ruan. The third edition: Beijing: Publishing House of Electronic Industry, 2011.

[2] Fergus R, Singh B, Hertzmann A, et al. Removing camera shake from a single photograph[J]., 2006, 25(3): 787-794.

[3] SHAN Q, JIA J, Agarwala A. High-quality motion deblurring from a single image[J]., 2008, 27(3): 1-10.

[4] Cho S, Lee S. Fast motion deblurring[J]., 2009, 28(5): 145: 1-145:8.

[5] Krishnan D, Tay T, Fergus R. Blind deconvolution using a normalized sparsity measure[C]//(), 2011: 233-240.

[6] CAI J F, JI H, LIU C Q, et al. Framelet-based blind motion deblurring from a single image [J]., 2012, 21(2): 562-572.

[7] XU L, ZHENG S C, JIA J. Unnatural L0 sparse representation for natural image deblurring[C]//(), Portland, 2013: 1107-1114.

[8] Oliveira J P, Figueiredo M A T, Bioucas D J M. Parametric blur estimation for blind restoration of natural image: linear motion and out-of-focus[J]., 2014, 23(1): 466-477.

[9] TANG S, GONG W G, LI W H, et al. Non-blind image deblurring method by local and nonlocal total variation models[J]., 2014, 94: 339-349.

[10] 徐焕宇, 孙权森, 李大禹, 等. 基于投影的稀疏表示与非局部正则化图像复原方法[J]. 电子学报, 2014, 42(7): 1299-1304.

XU Huanyu, SUN Quansen, LI Dayu, et al. Projection-based image restoration via sparse representation and nonlocal regularization[J]., 2014, 42(7): 1299-1304.

[11] MA Z, LIAO R, TAO X, et al. Handling motion blur in multi-frame super-resolution[C]//(), 2015: 5224-5232.

[12] PAN J S, HU Z, SU Z X, et al. L0-regularized intensity and gradient prior for deblurring text images and beyond[J]., 2017, 39(2): 342- 355.

[13] Schmidt U, Jancsary J, Nowozin S, et al. Cascades of regression tree fields for image restoration[J]., 2016, 38(4): 677-689.

[14] Krishnan D, Fergus R. Fast image deconvolution using hyper -Laplacian priors[R]. in Proc. Adv. Neural Inf. Process. Syst, Whistler, BC, Canada, 2009.

Multi-constraint Blind Restoration Method for Motion Blurred Image

LU Jing1，HU Gang2，QIN Xinqiang2

(1.,,726000,; 2.,,710054,)

Blind restoration of a motion-blurred image is a long-standing and challenging inverse problem. In order to estimate motion blur kernel (MBK) accurately and obtain a high-quality restoration image, a regularization-based multi-constraint blind restoration method for motion-blurred images is proposed. First, in order to extract the large-scale edges from the image accurately, a sparse image smoothing method, based on gradient selection, is proposed. Then, in the MBK estimation step, based on the inherent properties of the MBK, a multi-constraint regularization model, which combines the extracted large-scale image edges, is proposed. Finally, the multi-constraint regularization model, which is proposed in the MBK estimation step, is addressed by using a half-quadratic variable splitting scheme. Extensive experiments are performed on both synthetic blurred images and real-life blurred images. Experimental results indicate that in comparison with several recent successful representative image blind restoration methods, the proposed method is an improvement not only in terms of subjective vision, but also in terms of objective numerical measurement.

motion blurred image，blind restoration，large scale image edges，motion blur kernel，multi-constraint regularization model

TN911.73

A

1001-8891(2017)12-1098-09

2016-10-09；

2017-03-30.

卢晶（1983-），女（汉），陕西丹凤人，讲师，硕士，主要研究方向为图形图像处理、计算机辅助几何设计。

陕西省科技计划（工业攻关）项目（2014K05-22）。