对一道选择题的思考

章晓燕

[摘 要]在数学练习中，为了培养学生的数学思维，减少学生的无谓思考，必须回避有争议性的题目。通过对一道选择题的分析，指出教师应给学生多些建立在数学思考基础上的“无法确定”，少些咬文嚼字中的“无法确定”。

[关键词]数学本质；数学思维；数学思考

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2017）08-0036-02

【题目】笑笑和淘气放学后一起回家。走了一段路程后，笑笑对淘气说：“我已经走了全程的40%。”淘气说：“我已经走了全程的90%。”（ ）先到家。

A.笑笑 B.淘气 C.无法确定

这是六年级数学上册期中质量检测试卷上的一道选择题。乍一看，答案肯定是C，标准答案也正是C。这个是有道理的，两人的家与学校的路程是不确定的，即单位“1”不确定，所以不好确定谁先到家。

测试结果显示，大多数学生选择了B，就此，我和学生进行了交流：

生1：我选C，单位“1”不确定，不好比较。如果笑笑家离学校近有可能笑笑先到家，如果淘气家离学校近有可能是淘气先到家，如果两人离学校一样近也有可能两人同时到家。所以我选C。

师：有道理！（我将生1的理由重复了一遍）还有其他不同意见吗？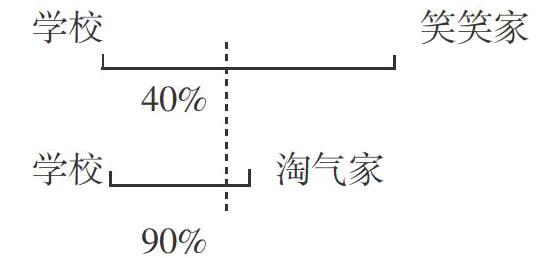

生2：我选B。如果笑笑先到家，或者无法确定，那么两人还能一起说笑吗？

生3：如果两人家很近，而且离学校一样远呢？我觉得，既然两人一块回家，单位“1”还能不一样吗？所以我认为是同时到家的。可是没有答案，所以我选了C。

师（故意激将）：看来选C很有道理。

生4：我有不同意见。单位“1”一样的话，一个走了全程的40%，一个走了全程的90%，两人还在一起说话，这说明全程的40%和全程的90%路程相同。既然相同，又说明单位“1”是不一样的。因此我选择B。

師：你们听懂了吗？（学生都摇头）

生5（突然站起）：其实只要他们的速度不一样，单位“1”再变化，都不好确定谁先到家。所以我认为应该选C。

虽然选C的学生很少，但其理由很充分；选B的学生不甘心，但苦于没有充分的理由。是否可以这样认为：选C的学生懂了，但选B的学生就是不理解呢？于是我想到了分类分析的方法。

（1）单位“1”相同。本题不能完成，并自相矛盾。如：

设笑笑家到学校的距离为x，淘气家到学校的距离为y ，因为两人在说笑，所以有40%x=90%y，x与y的比是9∶4。

显然，单位“1”不可能相同。

（2）笑笑家比淘气家离学校远。

明显的，淘气先到家。选B。

（3）笑笑比淘气近。由第一种情形的分析可知这个图无法画出。

综上所析，如果以（1）和（3）的情形确定本题答案，是否太过生活化？学生是否会进行这样复杂的思考？即使思考了，是否又违背了出题者的初衷？

单位“1”不管怎么变，我们都可以通过变换速度来控制答案，这样有意义吗？再说两人走路的速度是我们外人可以控制吗？显然是不可控的。试想，淘气看到笑笑的速度快了，他为什么不可以加快些速度呢？一直顺着这个思路想下去，本题就成了脑筋急转弯了。这样的不确定，不是我们所要追求的。

我本人认为第二种情形是最符合本题的答案。虽然与出题者的初衷不符，但这才是“人人学有价值的数学”理念的充分体现。

反观此题，显然该题在用词上是有瑕疵的，该怎么修改呢？笔者进行了一些尝试：

（1）笑笑和淘气抄写生字，他们每天写的字数一样多，两天后，笑笑完成了全部生字的40%，淘气完成了全部生字的90%，（ ）先写完。

本题考虑到了速度问题，但也有学生提出：既然都是老师布置的写生字，难道单位“1”会不一样吗？

（2）笑笑和淘气放学后回家，20分钟后，笑笑已经走了全程的40%，淘气已经走了全程的90%。若两人都按原来的速度继续行走，（ ）先到家。

本题基本考虑到了单位“1”和速度问题，较之原题和题（1）有了更严密的描述，但也有学生提出：前20分钟的速度谁快呢？

（3）笑笑和淘气放学后回家，走路的速度基本相同，20分钟后，笑笑已经走了全程的40%，淘气已经走了全程的90%。若两人都按原来的速度继续行走，（ ）先到家。

这样处理，题目就严谨了。

【思考】

一、注重数学本质，评价中增加变式练习

小学数学课程改革的最大变化就是例题基本从生活中来，其教学模式基本为：情景展现（从生活中来）——构建新知——应用知识（到生活中去）。

在“情景展现”环节一般都通过学生的生活和知识经验使学生产生思维冲突，然后引导学生从中理出新知。在这个环节中，教师往往要学生进行反复的讨论、探究、反思，在发现原有知识不能解释现有的现象时，学生就产生了学习新知的需求，养成了爱思考的习惯，并逐渐喜欢数学。但是，在操作过程中，教师往往忘了数学的本质——抽象。比如第二环节的“构建新知”，教师能够做到抽象，就是能将数学原型进行抽象概括，并将学生教会，到了第三个环节“应用知识”，教师就理解为新知回到生活，能解释生活现象即可，因此就觉得新教材“蜻蜓点水”，知识点不能进行“软着陆”。其实，第三环节的“到生活中去”不是单纯的解释应用，而是要高于生活。

比如，学习了“9的乘法口诀”后，在复习环节可安排习题：任意写出一个两位数（十位和个位不相同），然后将它们的位置调换形成新的数，最后用大数减去小数，你能发现什么规律？如：61-16=45，65-56=9，52-25=27……

这个习题是抽象的，与生活几乎没有联系，但却有很高的思考价值。

又如，四年级上册的“确定位置（一）”，教师将大部分时间都花在学生座位的确定上，而没有注重将知识抽象出来。我做了如下设计：

环节一：在白纸上摆☆，位置描述不统一，想到用方格。

环节二：在方格纸上摆☆，位置描述又不统一，想到用数字固定。

环节三：在格点上描述位置。（由格到点）

环节四：数对在实际生活中的应用（地图）。

这四个环节一环扣一环，环环递进，逐步抽象，比纠缠在座位确定的教学有效多了。

二、注重数学思考，评价中减少无谓争议

下面是几道有争议的题目：

（1）（判断）4比5，可以写出4∶5，也可以写成4/5。（六年级上册作业本）

教材已经删除了竖比的类型，学生一定会打“×”的。

（2）（判断）3+4+5可以写成3×4或4×3。（二年级上册作业本）

这道题曾经难倒了一大批数学教师。

（3）从1楼到3楼一共有几个台阶？（三年级下册数学教材）

事实上，房子的结构不一样，数台阶的方法也不一样。

教材上的练习题比较少，教师会去找些资料给学生练习，但教师往往没有多加筛选就使得很多没有价值但又有争议的题目出现在学生面前，造成学生“强词夺理”“自以为是”，这并不是数学教学的目的。

只有避开争议性题目，才能使学生往正确的思维方向和思维习惯靠拢，逐步使学生的思维向抽象角度靠近。因此，教师要给学生多些建立在数学思考基础上的“无法确定”，少些咬文嚼字中的“无法确定”。

（责编 金 铃）