探析高二数学中蕴藏的数学文化

■甘肃省秦安县第二中学 罗文军

探析高二数学中蕴藏的数学文化

■甘肃省秦安县第二中学 罗文军

2017年考试大纲修订后,在能力要求内涵方面,增加了对数学文化的要求——展现数学的科学价值和人文价值。下面通过赏析历年高考真题中的数学文化试题,来探析高考数学文化试题命题的视角。

一、取材于中国古代数学名著的高考数学试题

《九章算术》是我国古代经典数学名著,《九章算术》全书共246道算术应用题,分为九章:方田,粟米,衰分,少广,商功,均输,盈不足,方程,勾股。以《九章算术》中的问题为材料背景的高考真题,为高考注入了新的活力,很好地考查了同学们的数学素养,也潜移默化地增加了同学们的爱国主义情怀。

(2011年湖北卷理科第12题)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第5节的容积为____升。

分析:设出竹子自上而下各节的容积且为等差数列,根据上面4节的容积共3升,下面3节的容积共4升列出关于首项和公差的方程,联立即可求出首项和公差,再根据求出的首项和公差,利用等差数列的通项公式即可求出第5节的容积。

解:设该数列{an}的首项为a1,公差为d,依题意得:

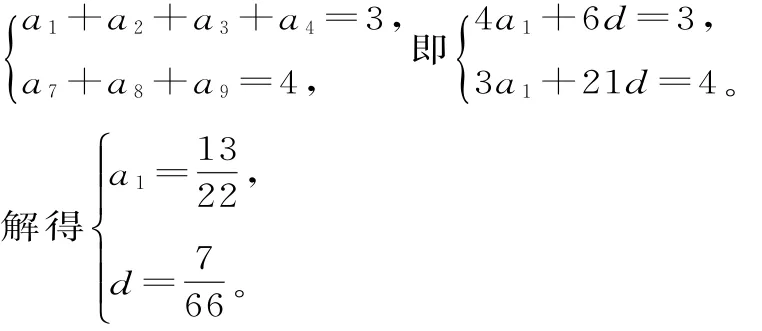
点评:此题源于《九章算术》第六章《均输》,考查了等差数列的通项公式,也考查了同学们的创新意识和应用知识能力。

这类数学文化试题,命题者直接取材于古代数学经典名著中同学们能够理解并且容易解决的简单问题,编制成数学试题,大多可以利用相关的基本知识轻松解决,通过这些试题体现我国古代数学成果的灿烂辉煌,也考查了同学们的理解能力和创新意识。

二、与黄金分割有关的高考数学试题

(1)双曲线的离心率e=____。

(2)菱形F1B1F2B2的面积S1与矩形ABCD的面积S2的比值

图1

解析:(1)由题意知|OA|=|OA2|,所以

所以e4-3e2+1=0。

(2)菱形F1B1F2B2的面积S1=

记∠B2F2O=θ,则sin

点评:本题以黄金双曲线为载体,考查直线与双曲线的位置关系和双曲线的离心率以及数形结合的思想。

2010年辽宁卷理科数学第9题同样以黄金双曲线为背景。

以黄金分割比为背景的高考数学试题,主要考查了同学们对高中有关基本知识的掌握情况,命题者通过这类试题,体现出了数学中的美学。

三、与斐波那契数列有关的高考数学试题

斐波那契(意大利数学家,约1170-1250)数列是由一个“兔子问题”引起的,即:假定一对大兔子每个月可以生一对小兔子,而小兔子出生后两个月就有生殖能力,问从一对大兔子开始,一年后能繁殖成多少对兔子。这就产生斐波那契数列:

1,1,2,3,5,8,13,21,34,…。

其规律是从第三项起,每一项都是前两项的和。用递推公式表达就是:

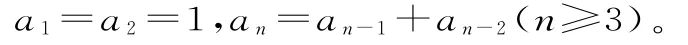
(2009年福建卷理科第15题)5位同学围成一圈依次循环报数,规定:

(1)第一位同学首次报数为1,第二位同学首次报出的数也为1,之后每位同学所报数的都是前两位同学所报出的数之和。

(2)若报出的数为3的倍数,则报该数的同学需拍手一次。

已知甲同学第一个报数,当5位同学依次循环报到第100个数时,甲同学拍手的总次数为____。

分析:根据题意可确定5位同学所报数值为斐波那契数列,可找到甲所报的数的规律,进而可转化为等差数列的知识来解题。

解:(1)将每位同学所报的数排列起来,即是“斐波那契数列”:

1,1,2,3,5,8,13,21,34,55,89,144, 233,377,610,987,…。

(2)该数列的一个规律是,第4,8,12, 16,…,4n项均是3的倍数。

(3)甲同学报数的序数是1,6,11, 16,…,5m-4。

(4)问题可化为求数列{4n}与{5m-4}的共同部分数。

易知,当m=4k,n=5k-1时,5m-4= 20k-4=4n。

又1＜4n≤100,故20k-4＜100,k≤5。

因此,甲拍手的总次数为5次,即第16, 36,56,76,96次报数时拍手,故答案为5。

点评:本题主要考查斐波那契数列、等差数列的知识。

(责任编辑 徐利杰)