数列中的创新题赏析

2017-03-23山东省文登第一中学

中学生数理化(高中版.高二数学) 2017年2期

关键词：那契关口正数

■山东省文登第一中学崔文

数列中的创新题赏析

■山东省文登第一中学崔文

创新题多以“新情境”为载体,从具体的问题情境中提取数学问题,或者渗透数学文化,考查同学们理解和运用新知识的能力,突出表现为将所学知识和方法迁移到新的问题情境中去。

1.定义“新概念”

对于数列{xn},若对任意n∈N*,都有成立,则称数列{x}n为“减差数列”。设数列{an}是各项都为正数的等比数列,其前n项和为Sn,且a1=1,

(1)求数列{an}的通项公式,并判断数列{Sn}是否为“减差数列”;

(2)设bn=(2-nan)t+an,若数列b3, b4,b5,…,bn是“减差数列”,求实数t的取值范围。

解析:(1)设数列{an}的公比为q。

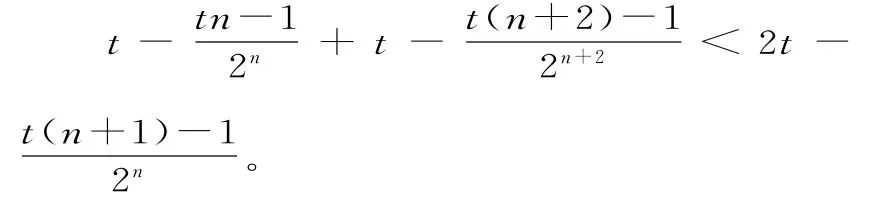
故t的取值范围是(1,+∞)。

点评:第一问考查等比数列的通项公式和前n项和公式;第二问套用新概念,最终转化为恒成立问题。

2.定义“新规则”

(1)设数列{an}的前n项和为Sn,若为常数,则称数列{a}为“吉祥数n列”。已知等差数列{bn}的首项为1,公差不为0,若数列{bn}为“吉祥数列”,则数列{bn}的通项公式为( )。

Ab.n=n-1 Bb.n=2n-1

Cb.n=n+1 Db.n=2n+1

(2)若一个数列的第m项等于这个数列的前m项的乘积,则称该数列为“m积数列”。若各项均为正数的等比数列{an}是一个“2017积数列”,且a1＞1,则当其前n项的乘积取最大值时,n的值为____。

解析:(1)设等差数列{bn}的公差为d(d≠因为b1=1,则即2+(n-1)· d=4k+2k(2n-1)d,整理得(4k-1)dn+ (2k-1)(2-d)=0。因为对任意的正整数n上式均成立,所以(4k-1)d=0,(2k-1)· (2-d)=0,解得所以数列{bn}的通项公式为bn=2n-1。

(2)由题可知a1a2a3·…·a2017=a2017,故a1a2a3·…·a2016=1。由于{an}是各项均为正数的等比数列且a1＞1,所以a1008a1009= 1,公比0＜q＜1。所以a1008＞1且0＜a1009＜1,故当数列{an}的前n项的乘积取最大值时,n的值为1008。

点评:第一问考查等差数列的前n项和公式;第二问考查等比数列通项的性质。“吉祥数列”和“m积数列”有别于“新概念”,其本质就是给定了一个新规则,基于新规则进行计算即可。

3.创设新情境

一位牧羊人赶着一群羊通过4个关口,每过一个关口,守关人将收走当时羊的一半,然后退还1只给牧羊人,过完这些关口后,牧羊人只剩下2只羊,则牧羊人在过第一个关口前有____只羊。

解析:记牧羊人通过第1个关口前、通过第2个关口前、…、通过第4个关口前剩下的羊的只数组成数列{an}(n=1,2,3,4),则由题意得1。而解得a=2,依次类推得

4a3=2,a2=2,a1=2。

点评:考查递推关系。要能够根据每次羊的数量变化,得出数列的项之间的递推关系。

4.渗透数学文化

意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1, 1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和,该数列是一个非常美丽、和谐的数列,有很多奇妙的性质,比如随着数列项数的增加,前一项与后一项之比越来越逼近黄金分割0.6180339887,人们称该数列{an}为“斐波那契数列”。若把该数列{an}的每一项除以4所得的余数按相对应的顺序组成新数列{bn},在数列{bn}中第2017项的值是____。

解析:1,1,2,3,5,8,13,…,除以4得的余数分别为1,1,2,3,1,0,1,1,2,3,1,0,…,即新数列{bn}是周期为6的周期数列,b2017= b336×6+1=b1=1,所以第2017项的值是1。

点评:本题考查数列的周期性。“斐波那契数列”是高中数学研究的一个很重要的数列模型,值得同学们深入思考。

巩固练习:

1.对于数列{an},定义数列{an+1-an}为数列{an}的“差数列”,若a1=2,{an}的“差数列”的通项公式为2n,则数列{an}的前n项和Sn=____。

答案:2n+1-2。

2.根据科学测算,运载神舟飞船的长征系列火箭,在点火后1min上升的高度为1km,以后每分钟上升的高度增加2km,在达到离地面240km高度时船箭分离,则从点火到船箭分离大概需要的时间是( )。

A.20min

B.16min

C.14min

D.10min

答案:B。

3.设数列{an}的前n项和为Sn,若对任意的正整数n,总存在正整数m,使得Sn= am,则称{an}是“H”数列。