立体几何与解析几何好题欣赏

■福建省龙岩市永定区城关中学 童其林(特级教师)

立体几何与解析几何好题欣赏

■福建省龙岩市永定区城关中学 童其林(特级教师)

或许,我们做了不少数学题,这些做过的题目在我们的心中留下的印象——有些深刻,有些容易忘记。印象深刻的题往往是我们认真思考研究过的,最终豁然开朗解出来的问题,或者绞尽脑汁仍然没有得出结果的题。如果我们以鉴赏的眼光来看待这些问题,反思这些问题,不仅能体会到题目的精彩,也能感受到思维的美、数学的美,进而提高解决问题的能力。下面在试题的百花园中采撷几朵出彩的题、让人回味的题,供同学们参考、欣赏和借鉴。

一、知识交汇，考查知识运用能力

棱长为2的正方体ABCDA1B1C1D1在空间直角坐标系中移动,若保持点A、B分别在x轴、y轴上移动,则点C1到原点O的最远距离为( )。

解析:建立空间直角坐标系,按照要求放置,只有C1与AB和O在同一个平面时,点 C1到原点O的才有最远距离,画出截面图形,利用两点距离公式求出OC1的表达式,通过三角函数的变换,求出最大值。

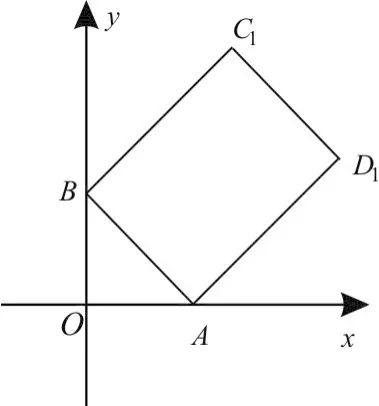
图1

如图1,设∠BAO =α,则C1坐标为(22sinα,2sinα+22cosα)。

因此,|OC1|

点评:立体几何问题转化为平面几何问题,是求最值问题时的常用方法,在此过程中引入辅助角,便可迎刃而解。

二、两点之间线段最短，考查数形结合的能力

数学里有一类问题,就是求最小值问题。求最小值问题,方法很多,有一种方法是利用两点之间线段最短来解决,这种方法在对称问题、沿几何体的爬行问题以及圆锥曲线的有关问题(主要是利用圆锥曲线定义)有很明显的体现。

如图2,已知点A(1,-1),点B(3,5),点P是直线y=x上的动点,当|PA|+|PB|的值最小时,点P的坐标是____

解析:连接AB与直线y=x交于点M,则当P点移动到M点位置时,|PA|+|PB|的值最小。

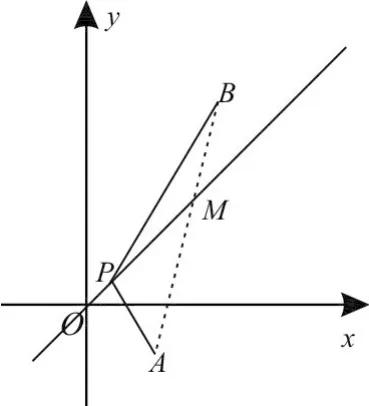
图2

于是当|PA|+|PB|的值最小时,点P的坐标为(2,2)。

点评:利用两点之间线段最短,是求最小值问题的一个思路。

变式训练1:已知点P是抛物线y2=2x上的一个动点,则点P到点A(0,2)的距离与点P到该抛物线准线的距离之和的最小值为( )。

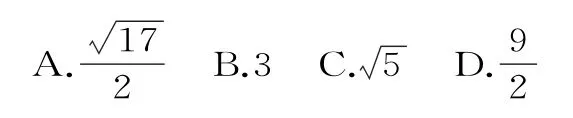
解析:根据抛物线定义,抛物线上的点P到焦点F的距离等于P到准线的距离,所以当P是线段AF与抛物线的交点时,所求的距离之和最小,此时|AF|=选A。

点评:圆锥曲线的最小值问题,往往结合定义求解。

三、解析几何里构造函数，考查转换化归能力

解析几何本身是通过代数关系来认识图形关系的,因此方程与函数、分类与整合等代数方法都能派上用场。

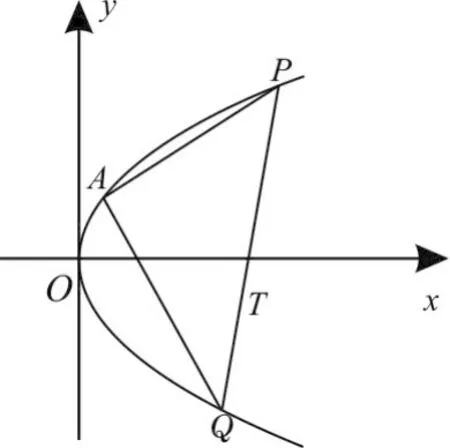
图3

如图3,已知抛物线C:y2=4x过点A(1,2)作抛物线C的弦AP、AQ。假设直线PQ过点T(5 -2),请问是否存在以PQ为底边的等腰三角形APQ。若存在,求出△APQ的个数;若不存在,请说明理由。

解析:假设存在以PQ为底边的等腰三角形APQ,设直线PQ的方程为x=my+n。

因为直线PQ过点T(5,-2),所以5= m·(-2)+n,n=2m+5。

直线PQ的方程为x=my+2m+5。

设点P,Q的坐标分别为P(x1,y1), Q(x2,y2)。

y2-4my-8m-20=0。

故y1+y2=4m,y1·y2=-8m-20。

设g(m)=m3+m2+3m-1,则g'(m)= 3m2+2m+3＞0,g(m)在R上是增函数。

又g(0)=-1＜0,g(1)=4＞0,故g(m)在(0,1)内有一个零点。

函数g(m)在R上有且只有一个零点,即方程m3+m2+3m-1=0在R上有唯一实根。

满足条件的等腰三角形有且只有一个。

点评:本题是存在性问题,和零点问题结合在一起,需要导数帮助,试题相对新颖,值得一做。

变式训练2:已知椭圆的中心在原点O,焦点在x轴上,点A(-2,0)是其左顶点,点C在椭圆上且

(1)求椭圆的方程;

(2)若平行于CO的直线l和椭圆交于M、N两个不同点,求△CMN面积S的最大值,并求此时直线l的方程。

解析:(1)设椭圆的标准方程为=1(a＞b＞0)。

(2)设M(x1,y1),N(x2,y2),若点C在第二象限,因为CO的斜率为-1,所以设直线l的方程为y=-x+m,代入可得:

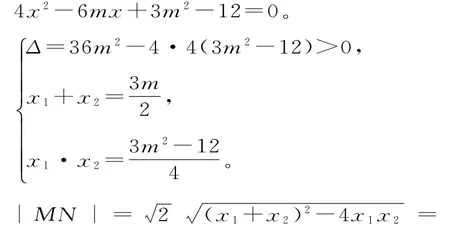
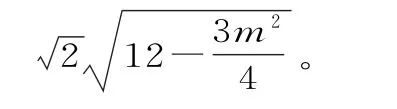
C到直线l的距离:

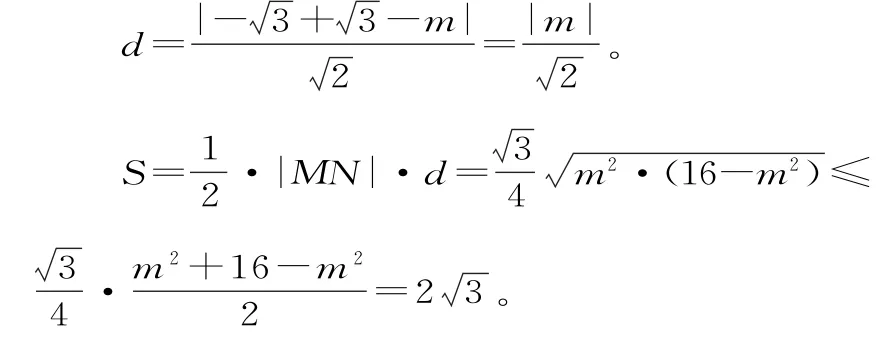
当且仅当m2=16-m2时取等号,此时m=±2满足题中条件。

若点C在第三象限,由对称性可知,直线l的方程为x-y±2=0。

点评:均值不等式在本题中的运用,是一个精彩之处。

四、动静转化，考查同学们灵活处理问题的能力

自然界的一切事物都在不停地运动着,静止是相对的。反映在数学上就是数量关系和空间形式经常地变换,而在变中又蕴涵着不变的因素,我们称之为“静”。发现动中的“静”和静中的“动”,并利用这些“动”和“静”解决数学问题,是数学的一个重要任务,并且显得非常有意义。

解析:如图4,不妨先固定A点,则问题转化为:在已知圆上找一点B,使|AB|最大或最小。此时由平面几何知识,可得直线AB必过圆心C。故要求|AB|的最大或最小,只需求|AC|的最值。而C固定,所以|AC|的最值容易求得。

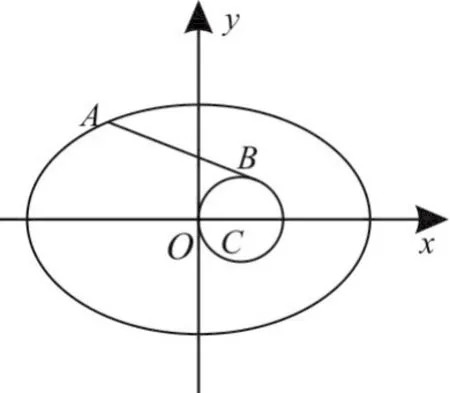
图4

圆C:(x-1)2+y2=1的圆心C(1,0),半径为1。

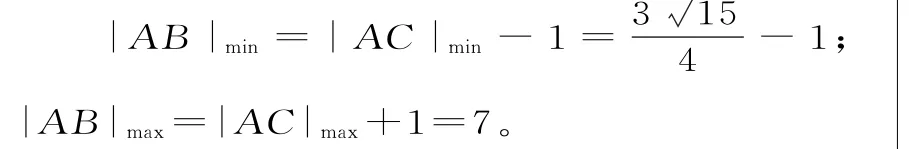
点评:若按常规思路,设出A、B的坐标代入距离公式,则复杂冗长,难以求出最值。因此必须改变思维方向,利用“以静制动”的思想,显得灵活有用。

变式训练3:点P在椭圆上运动,点Q、R分别在两圆(x-1)2+y2=1和(x+1)2+y2=1上运动,则|PQ|+|PR|的最大值为____,最小值为 。

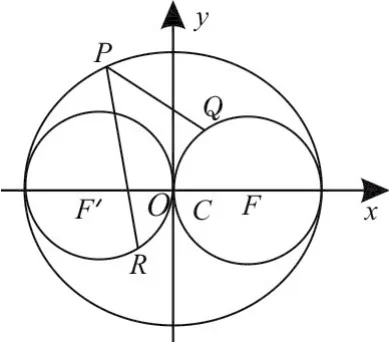
图5

解析:本题与上题又多了一个动点,若按常规思路,难以奏效。如图5,不妨也先固定点P,则问题转化为:求圆上两点Q、R与点P距离之和的最值。由平面几何知识可知,直线PQ,PR一定经过两圆心。要求|PQ|+|PR|的最值,只要求|PF|+|PF'|的最值。由于两圆心正好是已知椭圆的两焦点,故由椭圆的定义可知: |PF|+|PF'|为定值4。

所以|PQ|+|PR|的最大值为4+2= 6,最小值为4-2=2。

点评:概念是思维的细胞,定义是揭示概念内涵的逻辑方法,解题中利用定义应该成为我们的自觉。本题中,椭圆的定义发挥了重要作用。

(责任编辑 徐利杰)