数列问题的几个创新视角

■山东省沂源县第一中学 刘玉珍

数列问题的几个创新视角

■山东省沂源县第一中学 刘玉珍

数列是高中数学的重要内容,是高考的热点,也是进一步学习数学的基础,因此高考对这部分知识的考查题型多样,其中解答题的难度也较高。纵观近几年的高考试题,关于数列的考查主要有以下三个方面的内容:一是数列本身的知识,主要是等差(比)数列的概念、通项公式、前n项和公式;二是数列与其他知识的交汇,如与函数、方程、不等式、三角函数、解析几何等知识的结合;三是数列的应用问题,主要是增长率、分期付款等。下面介绍高考考查数列问题的新视角,供同学们学习时参考。

视角1：与组合交汇

是否存在等差数列{an},使等式对一切n∈N*成立?试证明你的结论。

思路：从特殊出发,推测一般,逻辑验证。

解析：假设存在等差数列,使题中等式对一切n∈N*成立,则n=1,2,3,4时该等式必成立,将n=1,2,3,4依次代入题中等式,可求得a1=2,a2=3,a3=4,a4=5。由此推测通项公式an=n+1,证明如下:

视角2：与向量、解析几何交汇

如图1,直线y=k x上有一系列点P1_,_P2,P3,…,Pn,…,已知n≥2时,设线段P1P2,P2P3, P3P4,…,PnPn+1的长分别为a1,a2,a3,…,an,且a1=1。

(责任编辑 王福华)

(1)求出a2,a3的值,并写出an的表达式(用n表示);

(2)设点M(n,an) (n≥2,n∈N),证明这些点中不可能有两个点在直线y=k x上。

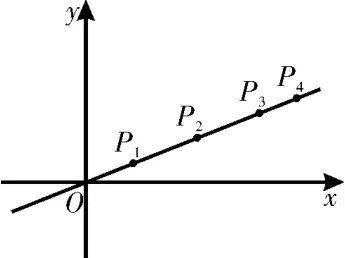
图1

思路：将已知的向量等式变形,得到一个关于向量长度的数列递推式。

解析：(1)由得

(2)假设A(m,am),B(t,at)两点均在直线y=k x上,其中m≠t。则有am=k m,且 at=k t,所以所以即所以m=t。这与m≠t矛盾,故在这些点M(n,an)(n≥2,n∈N)中不可能有两个点在直线y=k x上。

如图2,在直角坐标系x O y中,有一组对角线长为an的正方形AnBnCnDn(n=1,2,…),其对角线BnDn依次放置在x轴上(相邻顶点重合)。设{an}是首项为a,公差为d(d＞0)的等差数列,点B1的坐标为(d,0)。

(1)当a=8,d= 4时,证明:顶点A1、A2、A3不在同一条直线上;

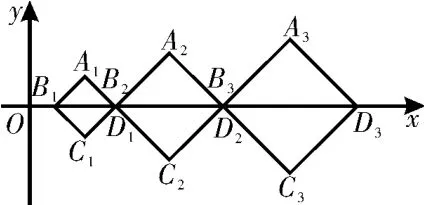
图2

(2)在(1)的条件下,证明:所有顶点An均落在抛物线y2=2x上;

(3)为了使所有顶点An均落在抛物线y2=2p x(p＞0)上,求a与d应满足的关系式。

思路：数列与解析几何相结合,常常通过点的坐标来联系。(1)要证三点不在同一条直线上,只要说明它们的斜率不相等就可以了。(2)要证明点在曲线上,就是要证明点的坐标满足曲线方程。(3)要使所有的点在曲线上,只要使第n个点的坐标满足曲线方程,就可以寻找到关系式。

解析：(1)由题意可知,A1(8 ,4), A2(1 8,6),A3(3 2,8),所以

因为kA1A2≠kA2A3,所以顶点A1,A2,A3不在同一条直线上。

(2)由题意可知,顶点An的横坐标xn=顶点An的纵坐标

因为对任意正整数n,点An(xn,yn)的坐标满足方程y2=2x,故所有顶点An均落在抛物线y2=2x上。

(3)解法1:由题意可知,顶点An的横、纵坐标分别是消去n-1,可得

为了使所有顶点An均落在抛物线y2= 2p x(p＞0)上,则有解得d=4p,a=8p。

故a、d应满足的关系式是a=2d。

解法2:点A1(x1,y1)的坐标为

因为点A1(x1,y1)在抛物线y2=2p x上,所以

又 点 A2(x2,y2)的 坐 标 为且点A2(x2,y2)也在抛物线上,所以由解得a=2d。

故a、d应满足的关系式是a=2d。

点评:对于数列与解析几何相结合的问题,这里是以正方形的对角线为数列的项,通过它得到An的坐标作为数列中的项,将数列与解析几何结合起来。这类题的综合性和探索性较强,知识的交汇清新自然且难度较大,能有效地考查深层次的数学品质和数学综合素质,因而极易在高考中出现。

视角3：与概率交汇

A,B两人拿一颗骰子每人连续抛掷两次做游戏(每抛掷两次算一次实验),规则如下:若掷出的点数之和是3的倍数,则由原掷骰子的人继续掷;若掷出的点数之和不是3的倍数,就换对方掷。第一次由A开始掷,设第n次由A掷的概率为Pn,求Pn的表达式(用n表示)。

思路：分类讨论确定Pn的递推关系,再求Pn的表达式。

解析：两颗骰子包含的基本事件共有6×6=3 6种,由题意可知,第n次由A掷有两种情况:

由于这两种情况是互斥的,因此Pn=,其中n≥2。

又P1=1,所以数列是以P-1为首项,为公比的等比数列。

(1)求P1和P2的值;

(2)求证:Pn+2-Pn+1=-

(3)求Pn的表达式。

解析：(1)P1为到达点(0,1)的概率,要到达(0,1)只有按向量a移动才可能,故。P为到达点(0,2)的概率,要到达

2(0,2)有两种方法,第一种直接按向量b可到达;第二种两次都按向量a走,故

(2)M点到达点(0,n+2)有两种情况:①从点(0,n+1)按向量a=(0,1)移动;②从点(0,n)按向量b=(0,2)移动。所以Pn+2=(Pn+1-Pn)。问题得证。

(3)由(1)(2)知{Pn+1-Pn}是以P2-P1=为首项,-为公比的等比数列,所以所以又因为所以Pn=

点评:递推问题是数列中的重点知识之一,本例若撇开概率知识,单纯地由Pn+2-,求 Pn的表达式,则其难度远低于高考中数列试题的平均难度,现一旦与概率知识交错综合,难度就大增,要不是(1)、(2)两问的引导与铺垫,我们一时难以想到用递推数列来求解。

视角4：与函数、不等式交汇

已知函数f(x)=l n(2-x)+ a x,在x∈(0,1)内是增函数。

(1)求实数a的取值范围;

(2)若数列{an}满足a1∈(0,1),an+1= l n(2-an)+an(n∈N*),证明:0＜an＜an+1＜1;

(3)若数列{bn}满足b1∈(0,1),bn+1= 2 l n(2-bn)+bn(n∈N*),问:数列{bn}是否单调?

解析：(1)对一切x∈(0,1)恒成立。当x∈(0,1)时,所以a≥1。

(2)由(1)知,当a=1时,f(x)在(0,1)上是增函数,所以f(0)＜f(x)＜f(1),所以0＜f(x)＜1。

要证0＜an＜1,可用数列归纳法:

当n=1时,a1∈(0,1)成立,假设当n= k时,有ak∈(0,1),则当n=k+1时,ak+1= l n(2-ak)+ak符合上述函数f(x)=l n(2-x)+x的条件,所以0＜ak+1＜1成立。故0＜an＜1成立。又an+1-an=l n(2-an)＞0,所以an+1＞an所以0＜an＜an+1＜1。

由0＜2-b2＜1,知b3-b2＜0⇒b3＜b2。

由b1＜b2,b2＞b3,知数列{bn}不单调。

点评:本题是一道很有味道的题目,特别是第(3)问通过特殊化来说明函数不单调。

视角5：与三角函数交汇

证明：要证α、β、γ成等差数列,因为α、 β、γ是锐角,只要证

所以α、β、γ成等差数列。

(责任编辑 王福华)