三角函数、数列与数学文化

■甘肃省天水市第十中学 方根太

三角函数、数列与数学文化

■甘肃省天水市第十中学 方根太

高中新课标把“体现数学文化价值”作为高中数学课程的十项理念之一,强调数学文化是贯穿整个高中数学课程的重要内容。三角函数、数列中常常这样考查数学文化。

一、取材数学图形

如图1是五角星,已知A C=a,则五角星外接圆的直径为____ (结果用含三角函数的式子表示)。

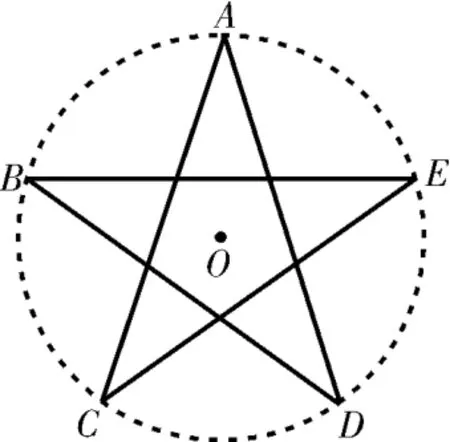
图1

解析：如图2,连接A O,并延长交圆O于点F,连接C F,则∠A C F=9 0°。因为A、B、C、D、E是圆O的五等分点,所以∠C A D=∠D B E=∠A C E =∠A D B=∠B E C。

又因为∠C A D+∠D B E+∠A C E+∠A D B+∠B E C=3 6 0°=1 8 0°,所以∠C A D=×1 8 0°=3 6°,所以∠C A F=∠C A D=1 8°。

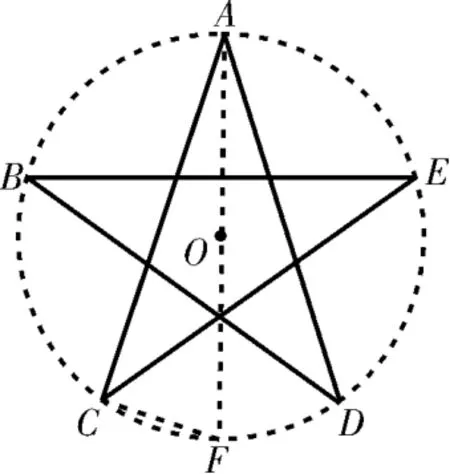
图2

点评:本题主要考查了圆周角定理、正五边形的性质、直角三角形中三角函数的定义。

二、取材数学时事

2 0 0 2年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图为基础设计的。弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形(如图3)。直角三角形中较小的锐角为θ,直角三角形的面积为4,小正方形的周长为8,则c o s(20 1 7 π+2θ)=____。

解析：设图中直角三角形较短的直角边为x。

因为图中小正方形的周长为8,所以小正方形的边长为2。

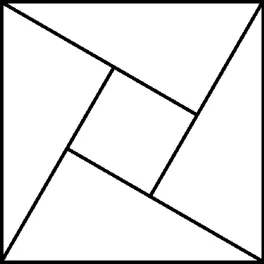
图3

所以c o s(20 1 7 π+2θ)=c o s(π+2θ)= -c o s 2θ=-(2 c o s2θ-1)=-。

点评:本题以2 0 0 2年在北京召开的国际数学家大会的会标为背景,考查了直角三角形的性质,以及三角函数诱导公式、二倍角公式。

三、取材数学名题

古希腊毕达哥拉斯学派的数学家研究过各种多边形数。如三角形数1,3, 6,1 0,…,第n个三角形数为记第n个k边形数为N(n,k) (k≥3,k∈N),以下列出了部分k边形数中第n个数的表达式:

正方形数:N(n,4)=n2;

六边形数:N(n,6)=2n2-n;

……

可以推测N(n,k)的表达式,由此计算N(1 0,2 4)=____。

解析：观察n2和n前面的系数,可知一个成递增的等差数列,另一个成递减的等差数列,推测故N(n,2 4)= 1 1n2-1 0n,所以N(1 0,2 4)=10 0 0。

点评:本题考查等差数列的性质,以及同学们的归纳猜想能力。

四、取材数学猜想

(角谷猜想)已知数列{an}满足: a1=m(m 为正整数),an+1=若a=1,则m所6有可能的取值为____。

解析：由题意知{an}中任何一项均为正整数,因为a6=1,若a5为奇数,则3a5+1=1,得a5=0,不满足条件。若a5为偶数,则a5= 2a6=2,满足条件。所以a5=2。若a4为奇数,则3a4+1=2,得,不满足条件。若a为

4偶数,则a4=2a5=4,满足条件。所以a4=4。

(1)若a3为奇数,则3a3+1=4,得a3= 1,满足条件。若a2为奇数,则3a2+1=1,得a2=0,不满足条件。若a2为偶数,则a2= 2a3=2,满足条件。若a1为奇数,则3a1+ 1=2,得a1=,不满足条件。若a为奇数,

1则a1=2a2=4,满足条件。

(2)若a3为偶数,则a3=2a4=8,满足条件。若a2为奇数,则3a2+1=8,得a2=,不满足条件。若a2为偶数,则a2=2a3=1 6,满足条件。若a1为奇数,则3a1+1=1 6,得a1=5,满足条件。若a1为偶数,则a1= 2a2=3 2,满足条件。

故m的取值可以是4,5,3 2。

点评:本题是著名的“角谷猜想”,考查分类讨论思想。注意对数列的首项a1为奇数和偶数两种情况进行讨论。

五、取材数学名著

《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3L,下面3节的容积共4L,则第5节的容积为( )。

解 析： 由 题 意 可 列 方 程 组解得所以

点评:本题主要考查等差数列的性质、通项公式与前n项和公式。

六、取材数学运用

生物节律是描述体温、血压和其他变化的生理变化的每日生物模型。表1中给出了在2 4h内人的正常体温的变化(从零点开始计时)。

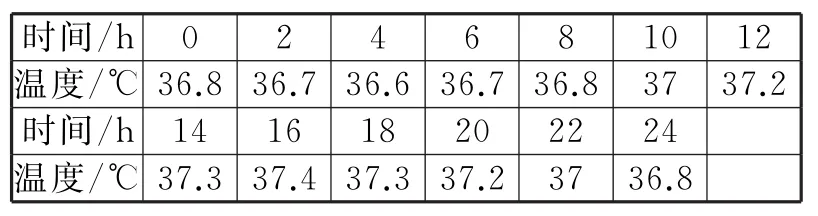
表1

(1)作出这组数据的散点图,并用曲线连接;

(

2)选用一个函数来描述体温y和时间t的函数关系;

(3)若测得某病人凌晨1:0 0的体温为3 8.2℃,问:该病人的体温比此时的正常体温高多少?(精确到小数点后两位)

解析：(1)根据这组数据作出散点图,并用曲线连接,如图4。

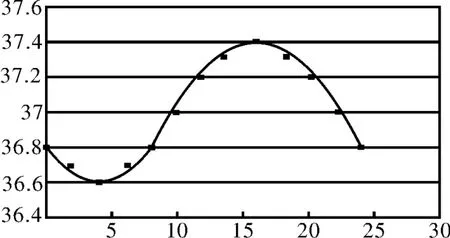
图4

(2)设 t时的体温为y=As i n(ω t+φ)+c,则c=?由取故可用来近似地描述这些数据。

点评:本题考查三角函数的图像与性质,考查同学们用数学知识求解实际问题的能力。

(责任编辑 王福华)