基于Seam型裂纹的复合型裂纹起裂角预测的有限元法

（海军航空工程学院 青岛校区，山东 青岛 266041）

基于Seam型裂纹的复合型裂纹起裂角预测的有限元法

王跃，穆志韬，刘涛，牛勇

（海军航空工程学院 青岛校区，山东 青岛 266041）

目的对处于多轴应力状态下的复合型裂纹起裂角进行预测。方法考虑材料的弹性性能，利用商业有限元软件ABAQUS中的Seam裂纹模拟穿透型裂纹损伤，建立双轴载荷作用下中心带孔边裂纹板的三维有限元模型，通过位移外推法得到裂纹尖端的应力强度因子（Stress Intensity Factor，SIF），并利用求得的SIF基于最大周向应力断裂准则预测孔边裂纹的起裂角。结果通过与相关文献结果进行对比，发现通过该有限元方法计算得到的应力强度因子与文献结果的最大误差在2%以内，预测的裂纹起裂角与文献结果的最大误差在3%以内。结论该有限元方法计算的裂纹起裂角与文献结果一致，因此文中求解复合型裂纹起裂角所使用的有限元方法是可靠有效的。

复合型裂纹；起裂角；Seam型裂纹；应力强度因子；最大周向应力准则

机身结构需要承受由飞行条件引起的机身剪力和弯曲力，开口损伤逐渐形成裂纹。这不仅对机身结构的使用功能和结构完整性产生消极的影响，甚至导致整个结构系统失效，酿成飞行事故。形成的裂纹依然处于多向载荷的共同作用下，裂纹的扩展往往表现为复合型裂纹的特点[1—4]。复合型裂纹的扩展不同于单纯张开型裂纹，具体表现在其扩展轨迹不再沿原裂纹的轨迹方向，而是与原裂纹方向成某一角度[1—12]。断裂力学是研究此类问题的有效手段之一，它是利用合适的断裂准则和应力强度因子（SIF）确定裂纹起裂角和裂纹扩展时的临界状态。Erdogan[5]等提出最大周向应力准则，假定裂纹沿最大轴向力扩展。Sih[6]提出最小应变能密度准则，对复合型裂纹的起裂进行了预测。Theocaris[7]等改进最小应变能密度准则，提出了裂纹沿着最大弹性应变能密度开裂的T准则。Khan[8]等对裂纹尖端的塑性区进行研究，发现裂纹的扩展路径与从裂纹尖端到弹塑性边界最短路径一致。由于建模能力强大，并可模拟复杂几何边界条件和本构关系等优点，有限元方法越来越成为工程人员所青睐的最有效的SIF求解方法。Henshell[9]等提出了四分之一结点奇异等参元，利用裂纹尖端附近的应力场（或位移场），进行回归分析、外推计算等方法间接获得裂纹尖端的SIF。杨绿峰[10]等对Williams级数进行了改进，建立了奇异域子单元的局部位移场，通过解Ⅰ-Ⅱ混合型Williams单元刚度方程求解应力强度因子。

有限元分析软件ABAQUS中有三种定义裂纹的方式[11—12]。Seam型裂纹可以求解裂纹尖端的应力应变场，但无法输出裂纹尖端的应力强度因子。使用Contour定义裂纹求解裂纹尖端SIF时，需要事先对裂纹扩展方向的相关参数进行设定，而裂纹的扩张方向对SIF的影响很大。使用XFEM定义扩展型裂纹预测扩展路径时，需要的材料断裂参数繁多，较难获得。文中利用Seam型裂纹受力后裂纹尖端的应变，采用位移外推法得到裂纹尖端附近的SIF，进行回归分析得到裂纹尖端处的SIF，并与相关文献进行对比。采用Erdogan等提出最大周向应力准则对裂纹的起裂角进行预测。

1 应力强度因子的求解

线弹性断裂力学中，SIF是分析裂纹扩展和失效的一个重要指标。文中利用裂纹尖端附近的位移场，使用外推的方法对裂纹尖端的SIF进行求解。机身结构件中的裂纹可以使用三维模型来研究，裂纹的三维模型中裂纹前沿任意点处局部坐标系和位移场如图1所示[13]。

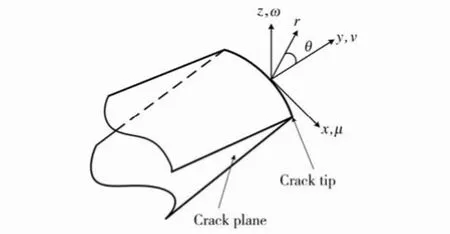
图1 三维模型中裂纹前沿任意点处局部坐标系和位移场

由图1可以看出，三维裂纹模型中裂纹前沿任意点处的局部直角坐标系由x，y和z三坐标轴构成，其中x-y坐标平面构成了裂纹前沿任意点处的法平面，y-z坐标平面则构成了裂纹前沿任意点处的切平面。模型中裂纹前沿任意点处的局部柱坐标系的三坐标轴为r，θ和z，柱坐标系下裂纹前沿任意点处的法平面由r和θ所构成。使用三维裂纹模型中的局部柱坐标系来表示局部直角坐标系下裂纹前沿任意点处的位移场，可得[13]：

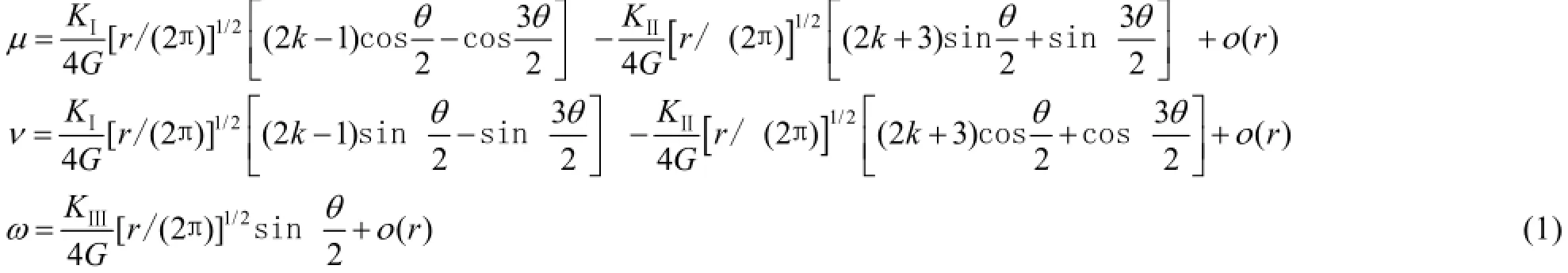
式中：μ，ν和ω分别对应于裂纹尖端局部坐标的位移；r和θ为计算点在局部柱坐标的坐标值；G为剪切模量；λ为泊松比，对于平面应力，k=3-λ/（1+λ），而对于平面应变，k=3-4λ；KⅠ，KⅡ和KⅢ分别为Ⅰ型Ⅱ型和Ⅲ型应力强度因子；()ro为高阶无穷小量。

根据式（1），若裂纹表面的位移已知，可以导出对称裂纹的应力强度因子计算公式[14—15]：

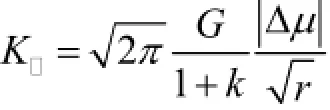
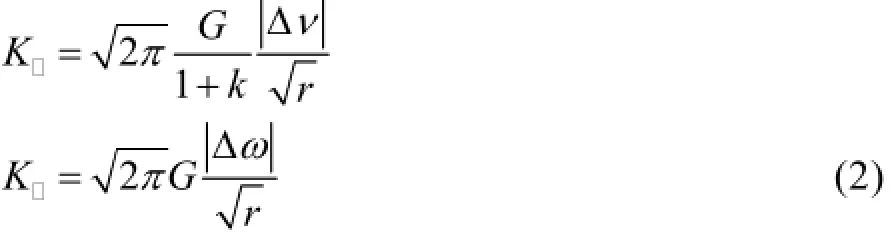
式中：Δμ，Δν和Δω为一裂纹面相对于另一裂纹面的位移。通过建立三维线弹性有限元模型，可以求解结构在单元节点处的位移及应力，将得到的位移代入式（2）就可求得该节点处的应力强度因子。通过对不同节点处的应力强度因子进行插值，就可以得到r→0时，KⅠ，KⅡ和KⅢ的值。

2 裂纹开裂角预测的断裂准则

利用Erdogan最大周向力断裂准则对复合型裂纹的初始起裂角进行预测。关于最大周向应力断裂准则的两个基本假设为[1,13]：

1）裂纹沿最大周向应力的方向起裂；

2）当此方向的最大周向力达到了临界值，裂纹失稳扩展。

由弹性力学和断裂力学的知识，可以得到Ⅰ-Ⅱ型复合型裂纹尖端的周向应力σθ表达式为：

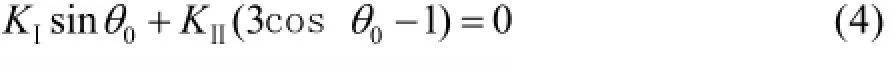
由式（4）解得起裂角为：

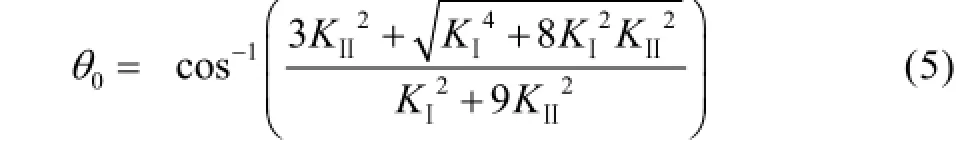
将位移外推法求得的裂纹尖端应力强度因子KⅠ和KⅡ代入式（5），即可求得裂纹的开裂角，结合有限元模型的裂纹尖端的应力分布特点，就可预测裂纹开裂的起始方向。

3 双轴载荷状态下裂纹起裂角分析

为了验证文中所描述的裂纹起裂角预测方法的有效性和准确性，对含孔边裂纹中心带孔板建立双轴载荷状态下的有限元分析模型，计算裂纹尖端的SIF和裂纹的起裂角，并将计算结果与文献[2]的计算结果进行对比。双轴载荷状态下含孔边裂纹中心带孔板结构模型如图2所示。

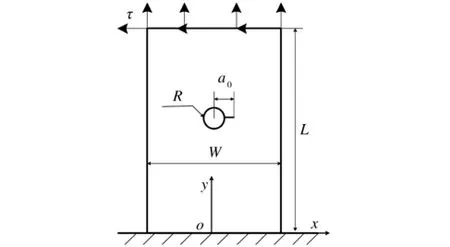
图2 含孔边裂纹中心带孔板的结构模型

选用双轴载荷下的300 mm（宽W）×400 mm（长L）×3 mm（厚tp）的中心带孔板模型，中心孔半径R=20 mm，孔边含有一初始裂纹长度a0=30 mm的平直裂纹。在模型的长度方向的一端施加σ=100 MPa拉伸载荷和τ=100 MPa剪切载荷，另一端固定，板宽度方向的两边自由。板的材料为2024-T3铝合金，其弹性模量E= 73 084 MPa，泊松比λ= 0.33。

采用ABAQUS 6.10建立中心带孔板的三维线弹性有限元模型。对板的建模采用适合弹塑性分析的C3D8R三维实体单元，这是由于该单元具有位移求解结果精确、不容易体积自锁等特点[12]。使用Seam型裂纹模拟孔边平直穿透型裂纹损伤，全局种子的尺寸设定为5 mm，在裂纹尖端处进行网格密度细化，设置局部种子的大小为0.25 mm，得到含孔边裂纹中心带孔板的有限元模型，如图3所示。

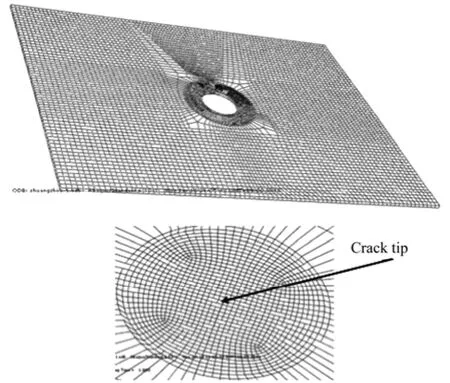
图3 含孔边裂纹中心带孔板有限元模型

选取裂纹尖端附近的单元节点，如图4所示。节点1为裂纹尖端，利用节点2和节点6、节点3和节点7、节点4和节点8、以及节点5和节点9四组点在x轴和y轴方向的位移差。通过式（2）可以求得沿裂纹方向距裂纹尖端不同位移处的KⅠ和KⅡ的值，并对其进行直线拟合，如图5所示，拟合后的方程为：

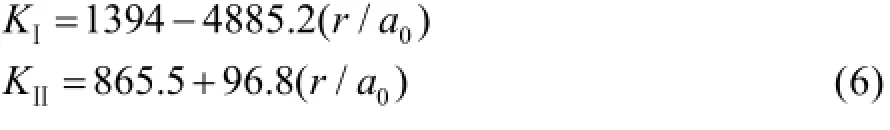
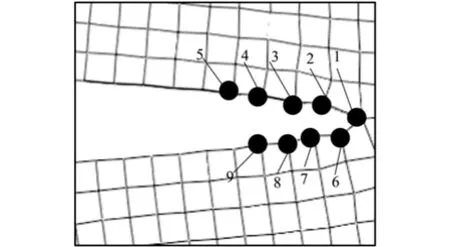
图4 裂纹尖端的节点

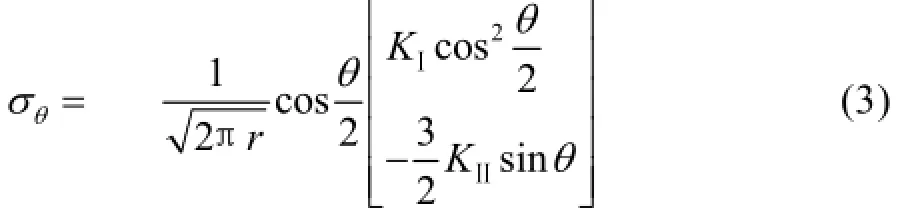
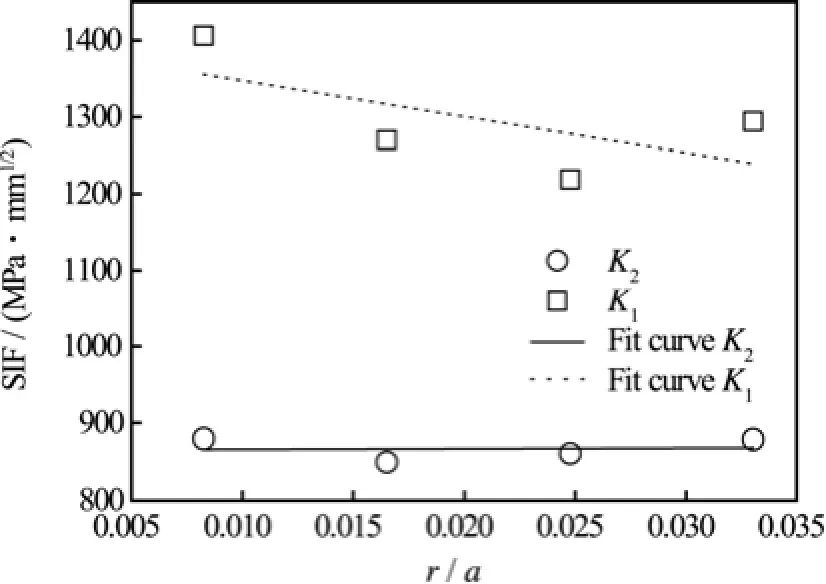
图5 沿裂纹方向距裂纹尖端不同位移处的应力强度因子拟合曲线

当r=0时，代入式（6）求得裂纹尖端的应力强度因子KⅠ=1394 MPa·mm1/2，KⅡ=865 MPa·mm1/2。为方便与文献[2]的结果进行对比，将应力强度因子无量，与文献[2]中FRANC2D模型的计算结果相比，相差1.4%和1.5%。说明文中使用的应力强度因子求解方法是有效的。

由于板的尺寸tp/W=0.01，属于薄板的平面应力状态，将计算的KⅠ和KⅡ的值代入式（6）可以求得裂纹的起裂角为44.7°。与文献[2]中FRANC2D模型的计算结果相比，相差2.82%。图6为有限元模型受力后的应力分布情况，可以看出，裂纹尖端处应力集中，应力分布呈8字形，裂纹将沿图中所标的方向开裂，这与文献[2]中的FRANC2D模型中的裂纹初始起裂方向一致。说明本文使用的裂纹起裂角的预测方法是有效的。

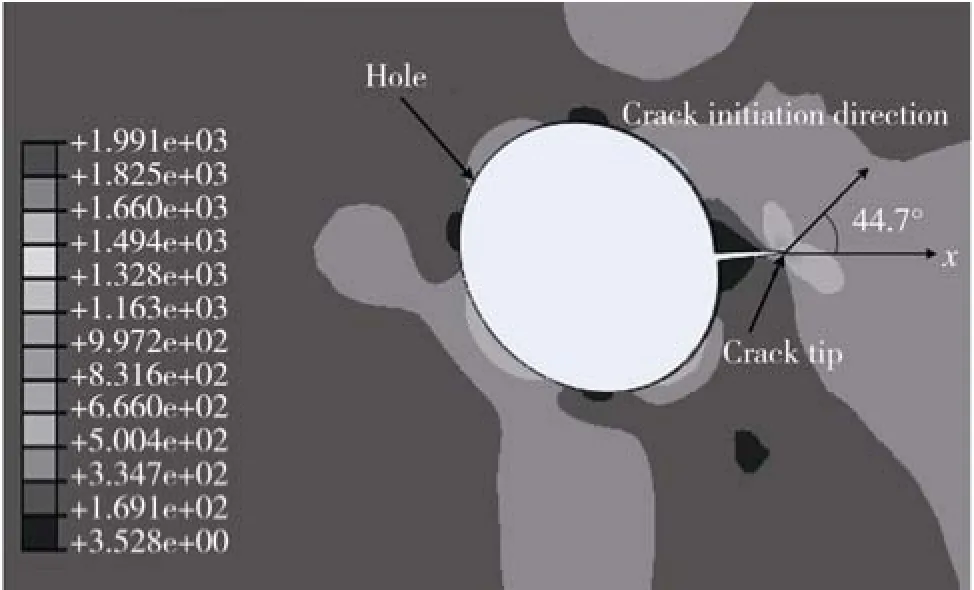
图6 有限元模型的应力分布

4 结语

建立了双轴载荷下含孔边裂纹中心带孔板的线弹性三维有限元模型，利用位移外推法求解了裂纹尖端的应力强度因子，基于最大周向力断裂准则，对有限元模型复合型裂纹的起裂方向进行了预测，预测结果与文献结果基本一致，文中的计算结果是可靠有效的。

[1] 詹福宇, 杨伟, 王生楠, 等. 基于Abaqus二次开发的机身开口损伤容限分析[J]. 机械强度, 2014, 36(1): 116—120.

[2] 张志贤, 王生楠, 詹福宇. 基于有限元的双轴载荷状态下自动裂纹扩展分析[J]. 航空计算技术, 2012, 42(2): 65—68.

[3] 马家升. 三维复合型裂纹应力强度因子有限元分析[D].哈尔滨: 哈尔滨工程大学, 2008.

[4] 翁剑成, 谢煌生. 复合型裂纹应力强度因子的有限元分析[J]. 龙岩学院学报, 2011, 29(2): 44—47.

[5] ERDOGAN F, SIH G C. On the Crack Extension in Plates under Plane Loading and Transverse Shear[J]. Journal of Basic Engineering, 1963, 85(4): 519—527.

[6] SHI G C. Strain-energy-density Factor Applied to Mixed Mode Crack Problems[J]. International Journal of Fracture, 1974, 10(3): 305—321.

[7] THEOCARIS P S, ANDRIANOPOULOS N P. The Mises Elastic-plastic Boundary as the Core Region in Fracture Criteria[J]. Engineering Fracture Mechanics, 1982, 16(2): 425—432.

[8] KHAN S M A, KHRAISHEH M K. A New Criterion for Mixed Mode Fracture Initiation Based on the Crack Tip Plastic Core Region[J]. International Journal of Plasticity, 2004, 20(1) :55—48.

[9] HENLLEN T K, BLACKBURN W S. The Calculation of Stress Intensity Factors for Combined Tensile and Shear Loading[J]. International Journal of Fracture, 1975, 11(4): 605—617.

[10] 杨绿峰, 徐华, 佘振平, 等. Willams单元分析Ⅰ-Ⅱ混合型裂纹应力强度因子[J]. 船舶力学, 2014, 18(1/2): 116—123.

[11] 徐慧, 伍晓赞, 程仕平, 等. 复合裂纹的应力强度因子有限元分析[J]. 中南大学学报(工程科学版), 2007, 38(1): 79—83.

[12] 石亦平, 周玉蓉. ABAQUS有限元分析实例详解[M].北京: 机械工业出版社, 2006: 151—169.

[13] 李庆芬, 胡胜海, 朱世范. 断裂力学及其工程应用[M].哈尔滨: 哈尔滨工程大学出版社, 2005.

[14] 王涛金, 车有金. Ⅰ-Ⅱ型复合裂纹初始开裂角的三角函数表达式及其相应断裂判据分析[J]. 中国锅炉压力容器安全, 2002, 19(4): 27—30.

[15] 王超, 朱哲明, 刘宏杰. 裂纹起裂角预测方法研究[J].四川大学学报(工程科学版), 2015, 47(2): 28—35.

Finite Element Method for Predicting Crack Initiation Angle of Mixed Mode Crack Based on Seam Crack Model

WANG Yue, MU Zhi-tao, LIU Tao, NIU Yong
(Qingdao Branch of Naval Aeronautical Academy, Qingdao 266041, China)

ObjectiveTo predict the initiation angle of mixed-mode crack under multiaxial stress.MethodsThe Seam crack in commercial finite element software ABAQUS was used to simulate penetrating crack damage according to elastic property of materials. A 3-D finite element model of center-hole with edge cracking plate under multiaxial stress was established. Displacement and extrapolation method and linear fitting method were used to calculate the SIF of crack tip. Initiation angles of cracks were predicted by maximum circumferential stress criterion, which were compared with those obtained by relative papers.ResultsThe maximum error of SIF between the result obtained by finite element models and that of document was within 2%, while the maximum error of initiation angles was within 3%.ConclusionThe results obtained by the finite element method in this paper are in line with document; therefore, the finite element method used for calculating the initiation angle of mixed-mode crack is reliable.

mixed-mode crack; crack initiation angle; seam crack; SIF; maximum circumferential stress criterion

10.7643/ issn.1672-9242.2017.02.021

TJ07

A

1672-9242(2017)02-0105-04

2016-08-24；

2016-09-04

王跃（1989—），男，山东人，博士研究生，主要研究方向为飞机结构腐蚀疲劳。