以苏教版为例谈谈对小学数学思考题教学的建议

谢利清

摘要：2014年新版的苏教版小学数学教材最大的亮点就是增加了一些思考题。这些思考题作为课程资源，为发展学生的思维能力和提高学生的学习兴趣，提供了很好的、可利用的材料。本文研究了教材中思考题的特点，并设计完善思考题，从而使思考题的教学能充分发挥其优势，促进学生发展。

关键词：苏教版；小学数学；思考题特点；设计

中图分类号：G623.5文献标识码：A 文章编号：1992-7711（2017）01-070-2一、苏教版小学数学教材中思考题的特点

（一）思考题概况统计

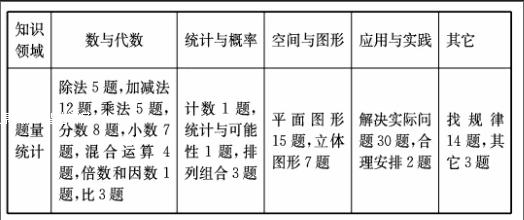
本套苏教版小学数学教材十二册共选编了122道思考题，在各册的分布情况如下：年级一年级二年级三年级四年级五年级六年级册次123456789101112题数121399118961291311从上表可知，思考题的数量在各年级各册次中分布较为均匀，其中一年级和六年级题量最多。这122道思考题，所涉及的知识面较广，根据题目内容的特点又作了如下的分类统计：知识

领域数与代数统计与概率空间与图形应用与实践其它题量

统计除法5题，加减法12题，乘法5题，分数8题，小数7题，混合运算4题，倍数和因数1题，比3题计数1题，统计与可能性1题，排列组合3题平面图形15题，立体图形7题解决实际问题30题，合理安排2题找规律14题，其它3题以上分类虽不很严格（有些题目可以归入不同类型，这里只归为其中的某一类），但从中能看出思考题所涉及的知识面，以及各类问题所占的大致比重。数与代数领域题量最多，其次是应用与实践领域，此外“找规律”这一类型的题目就有14题。苏教版小学数学教材中的思考题是遵循知识发展的逻辑顺序和学生身心发展的规律编排的，同一知识板块大多按学生年龄的高低、接受能力的差异而呈循序渐进、螺旋上升的模式被分散到各册教材中。

（二）思考题主要特点

1.注重思想方法的形成

知识的灌输对学生的影响只是暂时的，但数学思想方法的渗透对学生的影响却能收益终身。全套教材思考题类型可分为二十几类，需要用到的数学概念、方法、原理等规律性知识很多，归纳法、逆推法、构造法等均有所涉及，题量可谓少而精，起到了开阔视野，拓宽知识面的目的。如第三冊P28的思考题“找规律填数”先通过观察图形和算式的联系，再发现规律解决问题，用了归纳法。第二册P65的思考题：小红送给小明12枚邮票后，两人的邮票同样多，原来小红比小明多多少枚邮票，这题用了逆推法。这样的思考题具有趣味性、思想性，有利于提高学生的学习兴趣，还能培养学生学习的主动性，促进数学思维发展。

2.与知识点密切结合

数学教材内容是按知识的逻辑顺序和学生的身心发展规律来编排的，侧重于链状排列，系统性、理论性较强。思考题与必学内容联系，相互补充，既能使学生系统地学“深”，又能使学生联系实际学“活”；教材提供的思考题既能使学生复习前面的旧知识，又能为后面的新知识作铺垫。例如第六册第25页思考题：用载重2吨和载重3吨的货车各一辆运13吨苹果，可以怎样安排？此题将学生本单元所学的“吨”放入情境中，一方面可以帮助复习巩固本单元《千米和吨》的知识点，另一方面也可以为以后学习解决实际问题的策略一一列举埋下伏笔。学生在做这道思考题时，可以依次考虑载重2吨的运0，1，2，3……次，3吨的依次运几次，同时考虑到2吨和3吨的车运的总吨数等于13吨。

3.同类问题的编排集中与分散相结合

这一特点与教材编排特点是一致的，集中编排便于对教学内容进行概括、总结，形成系统，但有些内容需要多次循环，并且与其它知识的相互结合中，加强理解，提高认识，逐步抽象概括，完善知识结构。如“乘法”、“除法”、“找规律”等，这些内容宜于分散安排，逐渐提升。因而思考题中关于这方面内容的填数、巧算、填运算符号、找出规律等，不仅所占比重大，而且几乎涉及有思考题的教材的每一册。但认数、方程等，内容相对独立，因而采用集中编排的方式，易于总结规律。

4.以一般规律类推到一类问题

有一些思考题中隐藏着一般规律，通过挖掘内在特点，可以引伸或推广，达到解决一类问题的目的。像这类思考题比较适合于数学活动课教学。例如，第五册第25页思考题：把2、3、5、7四个数字分别填入□里，写成乘法算式。第一小题是要使积最大，应该怎样填？□□□×□；第二小题求要使积最小的填法。很显然，2与3、5、7中的7相乘积最大，3与2、5、7中的7相乘积最大，而5与2、3、7中的7相乘积最大，且两个乘数越大，积就越大，所以当填532×7时积最大。而要使积最小则两个乘数应尽可能的小，应填357×2。因此，对这类题，我们可以总结出这样的规律：两个乘数越大，积越大；两个乘数越小，积越小。对本题还可以作出进一步推广，如：要使商最大的填法，要使商最小的填法等等。

二、设计完善苏教版教材思考题的建议

（一）围绕教学重点设计思考题

每册数学教材里每单元都有重点和难点，开始就要让我们教师明确好重点和难点，每一单元可划分为几个“知识块”，同一“知识块”的几个教学课时又有不同的侧重点或“知识点”。思考题可以围绕每堂课的教学重点进行设计。

例如教学四年级上册“找规律——间隔排列”，重点难点是发现规律，运用规律解决实际问题。我设计了这样一道思考题：一只母鸡生蛋很有规律，总是连着两天每天生一个蛋，以后就要空一天不生蛋，已知1997年元旦这天没有生蛋，1997年全年一共生了（）只蛋。讲授时，我重点让学生发现母鸡生蛋的规律，第一天没生，所以规律排列起来是：没生，生，生，没生，生，生……三天为一组规律，1997年是平年有365天，所以365÷3=121（组）……2（天）。生蛋的个数就有121×2=242（个）。这道思考题紧紧围绕着教学重点“间隔排列”的规律进行设计，题中隐藏着的信息让学生发现规律，解决下“发现规律，并解决实际问题”这一教学难点。这样，学生在解决找规律类似问题时也能得心应手。

（二）激发学生学习数学的兴趣

兴趣是学习的前提，思维的动力。教材中的思考题往往可以创设好的“情境”引发学生的探索心理，穷追不舍，以致感到解数学题有一种妙不可言的意境，继续学习的信念油然而生。课后思考题是课堂教学的补充与深化，它基于所学内容又不限于所学内容，在学生能够接受的范围内灵巧设问，大大提高了问题难度，让学生有了继续钻研的动力。

例如第七册P69的思考题：小明和小刚同时各抛一枚硬币。这两枚硬币落地后如果朝上的面相同，算小明赢；朝上的面一正一反，算小刚赢。这样的游戏规则公平吗？孩子们都玩过抛硬币的游戏，现在抛硬币的问题调动起了他们的兴趣，使他们自然而然有了思考、解决问题的愿望，并在实现愿望的过程中掌握了相关知识。

（三）遵循认知规律设计思考题

多让学生观察后，让学生从中找到规律，然后进行练习。思考题要根据知识的结构特征和学生的认知规律进行设计，做到由浅入深，有层次、有坡度，一环套一环，环环相扣。

例如第四冊P80的思考题：小明、小华和小芳看一本同样的故事书。5天后，小明还剩34页没有看，小华还剩43页，小芳还剩26页。谁看的页数最多？谁看的最少？最多的和最少的相差多少页？分析：学生一看到这样的题会产生疑惑：故事书的总页数没有告诉我们，怎么求呀？很多学生认为无法解答此题。此时正是另辟蹊径、激发学生求异思维的好机会。教师应不失时机地引导学生转换角度进行数量关系的再思考，从而突破思维定势。如可问：“你可以先大胆假设一下这本故事书的总页数，再进行计算。”接着，让学生小组讨论交流，他们会发现：虽然每个人假设的总页数不一样，但是得到的结果却是一样的。这样思考分析后，学生会茅塞顿开，原来不需要知道总页数也可以求出答案：43-26=17（页）。

（四）多角度、多途径地训练发展思维

多途径、多角度地训练学生思维，开发学生智力，是提高学生个体素质的需要，是设计思考题的重要依据。设计多解题，训练学生思维的变通性。设计多变题（或多问题），训练学生思维的多向性。设计开放式习题，训练学生思维的广阔性。

总之，教师在数学思考题的教学中，要充分发挥数学思考题的趣味性、灵活性、综合性等特点，选用适合于学生的教学方法，激发学生学习数学的兴趣，发展学生个性特长，促进学生素质的全面发展。

[参考文献]

[1]赵言.从教材思考题谈数学素养的培养——小学数学也要重视数学思想方法的渗透[J].学科教学探索，2003（05）.

[2]叶文生.小学数学思考题有效教学的实践探索[J].小学教学参考，2006（Z5）.

[3]葛健芽.思考题解题策略例谈[J].小学教学研究，1999（04）.