土石坝变形监测平面模型方法研究与应用

寇清剑，陈建康，肖亚子，郭琴琴，裴 亮，董 渝

(1.四川大学水利水电学院 水力学与山区河流开发保护国家重点实验室，成都 610065；2.中国电建集团中南勘测设计研究院有限公司 工程科研院，长沙 410007)

土石坝变形监测是土石坝安全监控关键项目之一，在实际工程中，土石坝变形安全监测分析一般是通过单测点监测序列模拟分析，进而评估坝体运行状态。陈久宇[1]教授首先提出应用坝工理论选择统计模型的因子,结合实测资料,定量监控和评价大坝的运行安全。沈珠江等[2]提出线性模型、指数模型等函数模型来拟合大坝坝体的时效变形。有法国学者[3]在测值序列中分离出水压分量及温度分量，进而评判大坝运行的安全状况。上述模型均为单测点模型，无法考虑多测点间的相互关系，难以反映大坝的整体变形形态，因此，构建土石坝变形监测平面模型显得尤为重要。然而，由于在理论和方法上有所局限，对土石坝变形监测平面模型研究相对较少。吴中如等[4]研究得到了混凝土坝平面位移场监测模型。李珍照等[5]将拱坝坝体位移测点测值与测点空间坐标相结合，尝试建立拱坝空间模型。但土石坝变形极其复杂，在混凝土坝中适用的平面位移场方法难以直接用于土石坝的变形研究。为了从大坝整体变形状态评估大坝的运行安全，需要对土石坝变形监测平面模型做深入研究。

本文将克里金插值理论与方法应用于土石坝变形监测，建立了土石坝变形监测平面模型，并将该方法应用于某砾石土心墙堆石坝实际工程，模型精度较高，为类似工程提供参考价值。

1 土石坝平面模型构建

1.1 克里金插值原理

克里金数学模型建立在变异函数理论分析基础上，对一定边界范围内的区域化变量数值进行无偏最优估计。

时空位置用函数Z(h,t)=Z(x,y,z,t)表示，其中h=f(x,y,z)。对于待插点p，有：

(1)

式中：Z*(hp,tp)为待插点p的变形估计值；Z(hi,ti)为待插点邻域内已知点i的变形；λi为第i个已知变形测点的权重；n为已知变形测点的个数。

该方法不仅考虑了待插值点与附近已有的观测数据点空间位置关系，还考虑了各个相邻点之间的位置关系，利用已有观测值的空间分布结构特点，进行插值计算，其精度与传统方法相比得到较大提高，且符合实际[6]。

1.2 趋势性函数的选取

克里金法要求样本数据能服从二阶平稳过渡，且期望为常数。因此首先进行数据的趋势量剔除，再进行残差计算。常用的趋势性函数包括常量漂移、一次漂移和二次漂移。在土石坝的变形中，原观量包括趋势量和残差量两部分[7]。对此类数据的处理属于泛克里金的范畴，用空间信息来剔除趋势量，常分为两种：欧氏距离和空间坐标。

欧氏距离是指空间上两点最短的距离，欧氏距离n次漂移方法，是用欧氏距离h的n次多项式来拟合土石坝变形监测序列，拟合值即为变形趋势量，即：

(2)

式中：S(h)为与基准点相距h位置的趋势量；ai(i=0,1,n)为回归系数；n为漂移的阶数。

空间坐标对于二维坐标的二次漂移方法，表达式为：

S(x,y)=a0x2+a1y2+a2xy+a3x+a4y+a5

(3)

式中：S(x,y)为坐标为x、y位置的变形趋势量；ai(i=0,1,…,5)为回归系数。

通过对实际工程一个断面14个测点，运行期内2 a的沉降序列进行克里金插值，表1统计了2种趋势性函数精度对比情况。

表1 空间坐标和欧氏距离趋势法插值精度结果 %

从表1可以看出，总体数据显示空间坐标法剔除趋势量后，将大部分测点插值结果控制在10%以内，比欧式距离法精度高，故本文采用空间坐标法作为趋势性函数。

1.3 变异函数模型选取

克里金变异函数包括了球形模型、指数模型、高斯模型等[8]，各模型如公式(4)～(6)所示。

(1)球形模型：

(4)

(2)指数模型：

(5)

(3)高斯模型：

(6)

式中：h为分离距离；C0为块金值；C1为部分基台值；C0+C1为基台值；a为变程。

通过对实际工程一个断面14个测点原型观测序列2 d的测值作为样本，采用以上3种模型进行插值计算，表2统计了3个模型的计算精度。

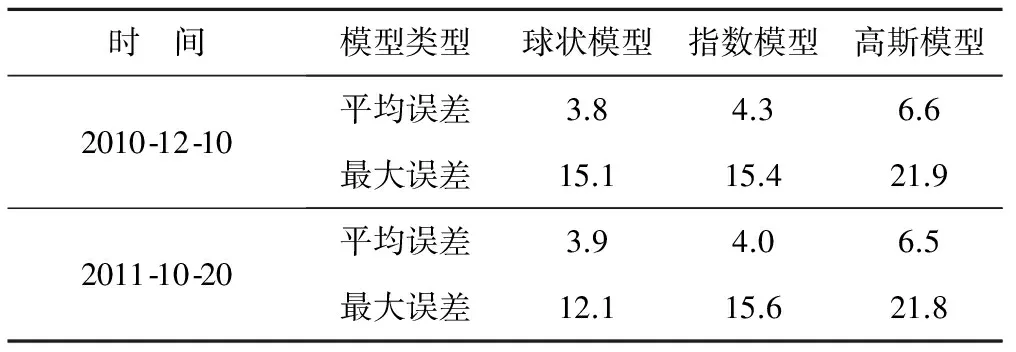
表2 变异函数模型精度统计 %

通过对每一个测点位置进行克里金插值结果与原观序列的对比，数据显示，球状模型精度高，故本文采取球状模型作为变异函数。

1.4 土石坝变形平面模型的构建

基于克里金法插值理论和方法，以大坝变形序列作为基础数据，采用二维坐标的二次漂移方法剔除序列趋势，用球状函数模型作为变异函数模型，构建土石坝变形平面模型。具体插值步骤如下。

(1)整理数据：将所有建模点的数据进行统计处理，统计所有预测点、建模点的空间坐标，预测点预测时间段内建模点的监测序列。

(2)剔除序列趋势：采用二维坐标的二次漂移法剔除建模点监测序列的趋势值，得到监测点监测序列的残差。

(3)插值：采用以球状模型作为变异函数的克里金插值模型进行插值计算，得到预测点的残差。

(4)位移预测与分析：计算预测点的预测值，并评价其精度。

2 工程应用

2.1 工程概况

某水电站工程为一等大(一)型，主要建筑物级别为Ⅰ级。拦河坝为砾石土心墙堆石坝，坝顶总长540.50 m，最大坝高186 m，坝基覆盖层最大厚度为75.36 m。水库正常蓄水位850.00 m，库容53.37 亿m3，调节库容38.94 亿m3，工程于2007年4月开始坝体填筑，填筑过程连续，2009年9月填筑到坝顶，之后进入正常蓄水运行期。

该土石坝变形监测采用断面和单点方式布置，水平位移采用引张线式水平位移计进行变形监测，竖直位移采用水管式沉降仪进行监测，本文计算中采用大坝0+240和0+310两个断面共31个测点，由于测点CH13、CH16、CH25损坏，无法获得其准确监测序列，故本文选取监测序列相对完整的28个测点进行变形监测分析与预测。0+240断面与0+310断面测点分布图如图1和图2所示。

2.2 基于克里金插值原理的土石坝变形平面模型

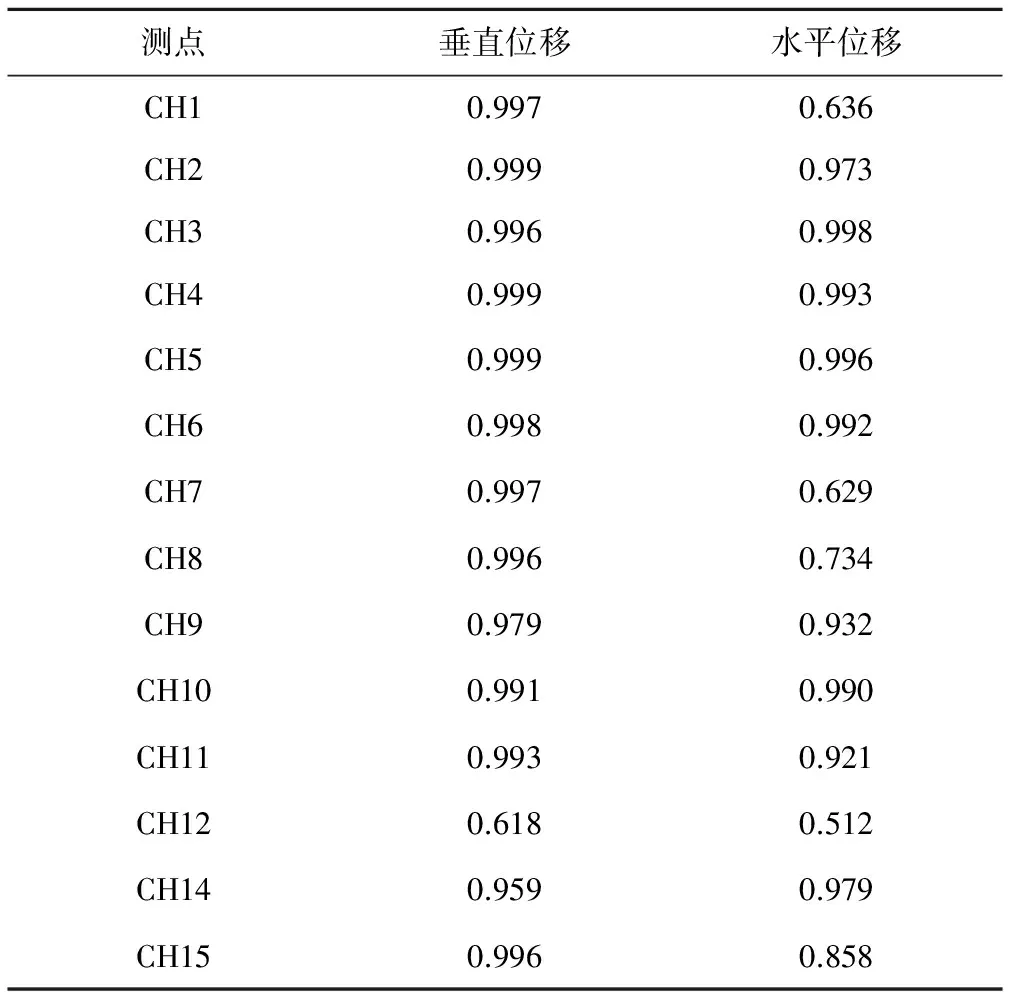
取该工程的0+240和0+310两个断面，分别建立变形平面模型。以2010年2月到2011年12月变形监测序列值为基础，分别以每一个测点为预测点，该断面其他测点为建模点，通过克里金插值计算进行测点变形预测，用预测值与原观序列进行比较分析。表3统计了0+240和0+310两个断面的沉降与水平变形样本测点预测值与原观序列的平均误差，表4统计了0+240断面预测值与原观序列的相关系数，图1和图3分别显示了0+240断面2010年10月3日沉降变形与水平变形，原观测值与克里金插值结果分布图。

表3 平面模型精度结果统计 %

图1 0+240断面测点分布、2010年10月3日沉降原观测值与克里金插值结果分布图(单位：mm)Fig.1 Distribution of measuring points in 0+240 section, and the original observations of the settlement and the distribution of Kriging interpolation results on October 3, 2010

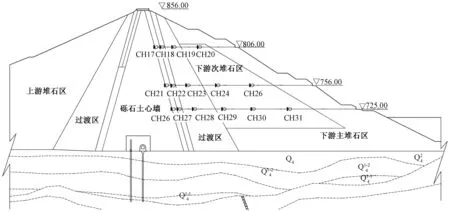
图2 0+310断面测点分布图Fig.2 0+310 section measuring point distribution map

图3 0+240断面2010年10月3日水平变形原观测值与克里金插值结果分布图(单位：mm)Fig.3 On October 3, 2010, original observation of horizontal deformation and distribution of Kriging interpolation result in 0+240 section

测点垂直位移水平位移CH10．9970．636CH20．9990．973CH30．9960．998CH40．9990．993CH50．9990．996CH60．9980．992CH70．9970．629CH80．9960．734CH90．9790．932CH100．9910．990CH110．9930．921CH120．6180．512CH140．9590．979CH150．9960．858

[9-12]精度分析方法，精度结果显示：①沉降变形大部分测点误差在10.0%以内，相关系数大部分测点大于0.9，模拟精度高；②水平变形大部分测点误差在15.0%以内，相关系数70%的测点大于0.8，模拟精度较高；③从0+240断面某时刻沉降变形、水平变形原观测值与克里金插值结果分布图结果显示，插值所得结果符合土石坝变形规律，模型精度较高。

2.3 影响空间模型精度的因素分析

克里金插值是基于已知点之间的欧氏距离和各点属性值(变形量)来计算各已知点对待插位置的权重值，因此，监测点间的欧式距离以及变形量对模型的精度影响很大。

取水平变形测点CH1作为研究对象，以2010年10月3日的监测数据进行分析。如表5所示，将各已知点权重系数与变形值的乘积除以待插点的插值结果得到各建模点贡献比例。

通过表5可知，CH2和CH5对CH1测点影响最为明显，因此在克里金插值方法应用中，对待插点影响最大的是周边已知点，故应用克里金插值时需注重测点位置和测值的选取。

3 结 语

本文基于克里金法对土石坝变形平面模型的深入研究，得到以下结论：

(1)通过对克里金插值趋势性函数的分析认为基于空间点的空间坐标法剔除变形序列的趋势值，比单纯用欧氏距离法效果更理想。

(2)从克里金插值变异函数模型选取分析认为球状模型能更好地构建土石坝变形监测二维平面模型。

(3)在克里金插值方法中，欧式距离和变形量是影响土石坝变形平面模型精度的两个主要影响因素，在实际应用中要注重测点位置和测值的选取。

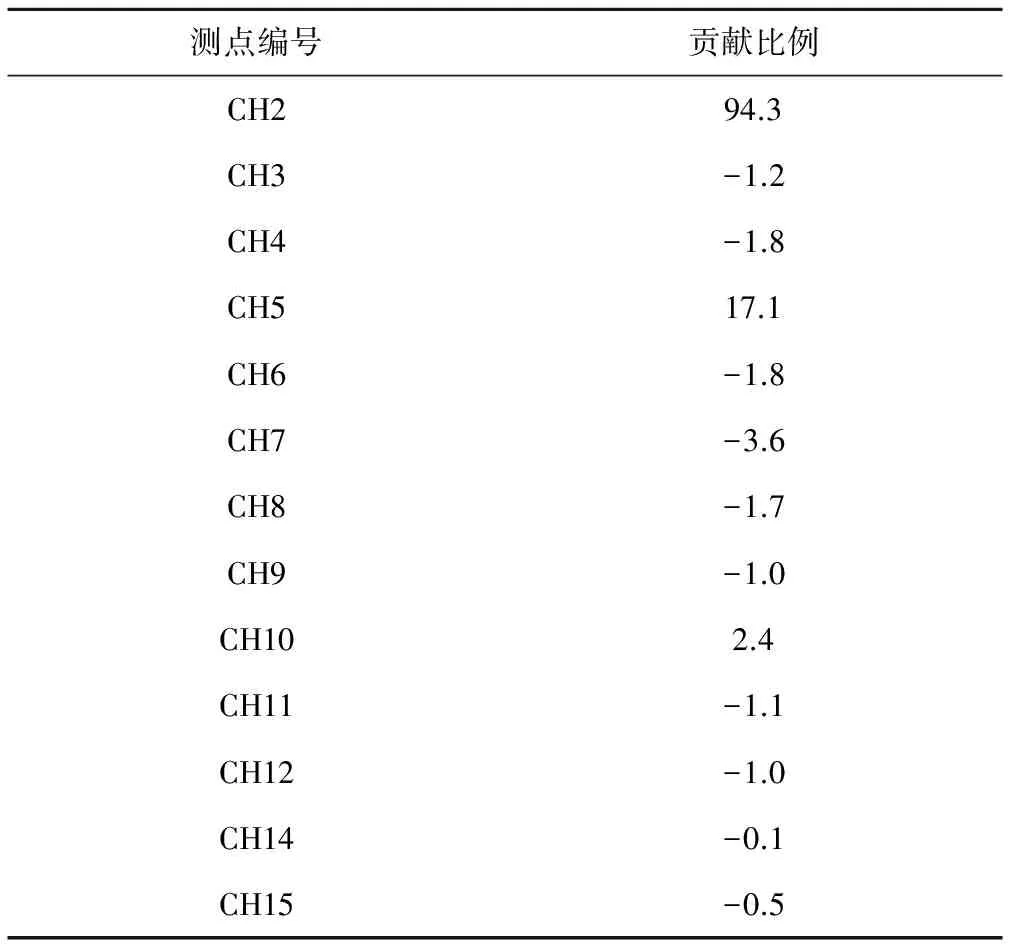
表5 水平变形CH1测点克里金插值各建模点贡献比例统计 %

(4)基于克里金插值原理，构建的土石坝变形平面模型，插值结果符合土石坝变形规律，具有良好的插值精度，原理简单，模型构建方便，具有良好的工程应用价值。

□

参考文献：

[1] 吴中如,顾冲时,沈 振，等.大坝安全综合分析和评价的理论、方法及其应用[J].水利水电科技进展, 1998,(3):5-9.

[2] 沈珠江，赵魁芝.堆石坝流变变形的反馈分析[J].水利学报，1998，(6)：1-6.

[3] 袁晓峰.大坝安全监测资料分析若干问题研究——万安电厂典型坝段监测资料分析[D].南昌:南昌大学，2007.

[4] 顾冲时，吴中如，蔡 新.拱坝动态空间位移场的混合模型研究[J].工程力学，1996，(S):376-380.

[5] 李珍照.大坝安全监测[M].北京:中国电力出版社,1997.

[6] 王建民.基于Kriging下的移动曲面拟合法研究[J]. 测绘科学,2012,(4):160-161.

[7] 周正军.高心墙堆石坝变形预测模型与变形调控技术研究[D].成都:四川大学,2015.

[8] 翟进乾.克里金(kriging)插值方法在煤层分布检测中的应用研究[D].太原：太原理工大学,2008.

[9] Qinqin Guo, Liang Pei,Zhengjun Zhou, et al. Response surface and genetic method of deformation back analysis for high core rockfill dams[J]. Computers and Geotechnics, 2016,74:132-140.

[10] 姜景山. 土石坝安全监测资料分析评价方法研究[D]. 郑州：郑州大学,2005.

[11] 刘正云,汪新槐. 土石坝变形数学模型研究[J]. 大坝观测与土工测试,1999,(6):5-8.

[12] 李啸啸,程黎明,蒋 敏，等. 土石坝外观变形统计模型时效因子函数探讨[C]∥ 2012年中国水力发电工程学会大坝安全监测专委会年会暨学术交流会论文集，2012.