基于数值模拟的地下水开采引起的地面沉降机理和对策研究----以定襄县贾家庄为例

盛登宝，吕义清

(太原理工大学 地球科学与工程系，太原 030024)

0 引 言

过度抽取地下水引起的地表不均匀沉降，影响地表建筑物、道路、管网等设施的安全，所以，开展地面沉降的研究，分析其产生沉降的原因以及动态降水的时间与空间效应具有重大的现实意义。抽取地下水过程中引起的固结变形是一个典型的三维渗流固结耦合问题，国内外许多学者开展了大量的理论和实践研究。

研究表明，地下水在含水层孔隙内流动时，导致孔隙水压力的变化，会引起与土骨架变形有关的应力变化，同时改变岩土体的物理力学性质[1,2]。前人在岩土体流固耦合分析方面已经做了大量研究[3-6]，本文借助Comsol Multiphysics有限元数值模拟软件，基于biot固结理论，结合弹塑性力学理论和渗透力学理论，建立数值模型进行求解，得出了大量抽取地下水情况下地表变形位移情况以及含水层水头、土体孔隙水压力分布情况，为地质灾害预防提供一定的帮助和技术指导。

1 固结数学模型

1.1 基本假设

(1)土骨架线弹性，变形微小；

(2)土颗粒和孔隙水均不可压缩；

(3)渗流符合达西定律；

渗流场变化过程则主要基于达西定律形式的连续方程来描述，即：

▽·(-K▽H)=0

(1)

式中：Sh为存储系数，m-1；K为渗透系数，m/s；H为水头，m。

将方程(1)中水头用孔压表示进而转化为方程(2):

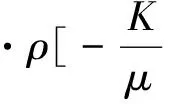
(2)

式中：S=Sh/(ρg)；H=P/(ρg)+D；K=κρg/μ。

1.2 基本方程

(1)平衡方程。假设一均质，各向同性的饱和土单元体dxdydz，若体力只考虑重力，z坐标向上为正，以土体为隔离体则三维平衡微分方程为：

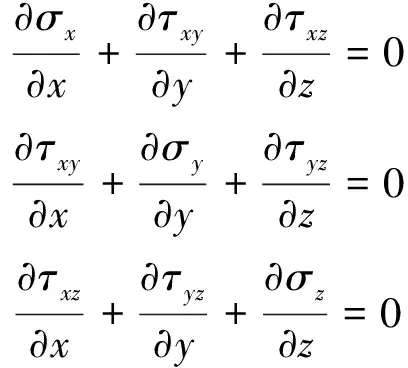
(3)

(2)本构方程。Biot理论最初假设土骨架为线弹性体，服从广义胡克定律，根据弹性力学本构方程，应力用应变来表示：

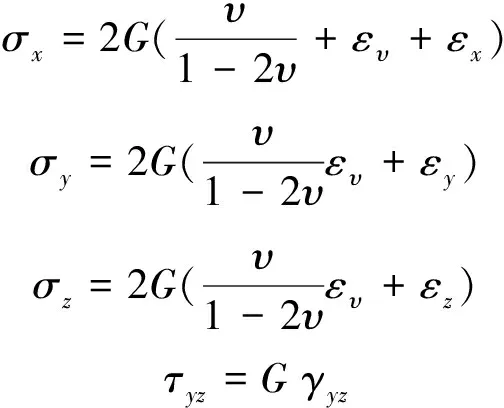
(4)

式中：G、υ分别为剪切模量和泊松比；ευ为体应变ευ=εx+εy+εz。

(3)几何方程。用几何方程将应变表示成位移，设x、y、z方向的位移为us、vs、ws在小变形的假定下，6个应变分量为：

(5)

式中：εx,εy,εz为x、y、z方向的正应变。

(4)固结微分方程。将(4)和(5)带入(3)中就可以得到以位移和空隙压力表示的平衡微分方程：

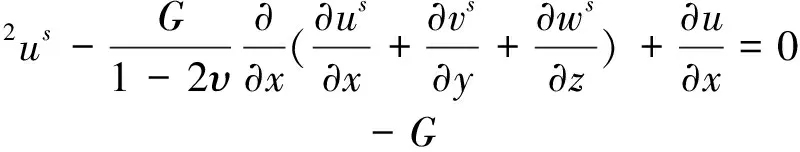
(6)

上面方程中有4个未知量us,vs,ws,u，求解还需要一个方程，由达西定律得：

▽2u

(7)

展开用位移表示得：

▽2u=0

(8)

式中：K为渗流系数；γw为水的容重。

公式(6)、(8)便是Biot固结方程。

2 应用实例

2.1 工程概况

贾家庄村位于山西省定襄县西北部，村庄东侧有1眼抽水井，井深130 m，井口直径30 cm。地下水位埋深较浅，含水层为泥河湾组、午城组、离石组黄土层中的砾石层、流沙层及钙质结核层、中—粗砂层，地下水主要接受河水及大气降水补给。不良地质现象主要为由于地下水的过量抽取引起了沉积层固结压缩，引起地表沉降变形，最后造成居民房屋严重破坏，见图1。

图1 贾家庄地面沉降房屋变形破坏图

2.2 模型的建立

根据该矿区的地层资料，建立长为1 000 m、宽为1 000 m、高为130 m的三维模型，共三层，厚度从上至下依次为40、10、80 m。在抽水井的设定中，本文采用杆单元来描述抽水井，它能精细的控制实际流量，很好的反映动态降水的时间与空间效应，与采用定水头的点模拟抽水井的方法相比，此处理方法考虑了尺寸效应对模型的影响。

2.3 边界、初始条件、参数

结合定襄县水文地质资料，确定了岩土体物理力学参数(表1所示)。模型中流体的密度为1 000 kg/m3；黏度为1×10-3Pa·s；流体压缩率为4×10-101/Pa。通过从最低含水层抽取地下水来降低含水层，抽水井日出水量约8 200 m3/d，所以本模型直接将抽水边界的水头定为H=-3 (m/a)*t，即假设水以平均3 m/a的渗透速度流动，且渗流场从初始即进入稳定状态，10年时间保持不变。而影响模型分析计算的主要因素是水头的变化而不是水头值自身，所以本模型直接将表层的水头定为H0=0 m，这样处理可避免随时间变化要不断变化表层水头边界的麻烦。这种处理方法便于建立初始边界条件。结合实际监测情况，在计算模型中距抽水井0、250、500 m位置分别添加3个域点探针来模拟实际监测。

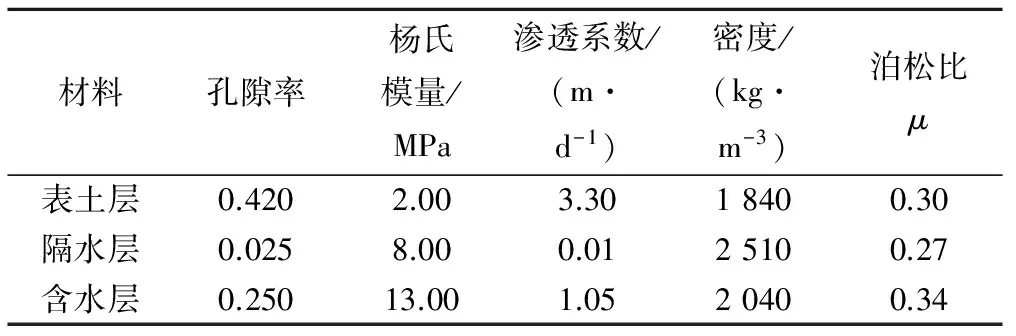
表1 岩层物理力学参数

2.4 计算结果及分析

地面沉降是土层中孔隙水承担的孔隙水压力和土骨架承担的有效应力发生变化的结果。处于平衡状态的含水系统，当地下水被抽出后，孔隙水压力减小，原先的土、水平衡状态被破坏，有效应力发生变化土体产生变形，且土体的力学性质、贮水性和透水性都将随之变化。地面沉降是土和水相互作用、内部应力发生变化的外在表现，它与土的变形特性和水的渗流情况密切相关。

多物理场耦合分析软件Comsol Multiphysics中的多孔弹性物理场接口建立的地下水抽取—地面沉降流固耦合模型，实现了达西定律场和固体力学场的真耦合，能够精确反映动态降水的时间与空间效应；通过多孔弹性物理场接口，建立流固耦合模型，模型的求解时间为10 a，1 a为一个时间步。

经过计算分析得出地面及地下水时空效应变化。如图2所示，该结果为10 a(现如今)后地面沉降结果，抽水后，地下水水位下降，在抽水井周围产生较大的水力坡度，随着水力坡度的增大，相应地渗透压力也增大。在地下水自上而下的渗透过程中，地表变形，形成降落漏斗，表现为在地面呈以降水井为圆心的同心圆分布，影响半径约300 m。图3为t=10 a地面沉降二维剖面图，矿井抽水区域漏斗中心沉降最大为Smax=1.19 m。

图2 t=10 a，Z方向地面沉降位移图

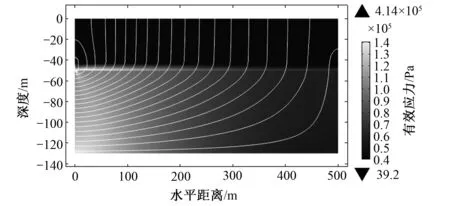
图3 t=0～10 a，地面沉降总位移二维剖图

由于土体是由固体颗粒(固相)、水(液相)和空气(气相)三部分组成，作用在土体上的应力是通过颗粒间的接触和孔隙水来传递的。由颗粒间接触点传递的应力是对土体变形和强度有效的粒间力，称为有效应力。由孔隙水传递的应力称为孔隙水压力，它仅对土颗粒产生压缩，由于固体颗粒的压缩模量非常大，可以认为是不可压缩的，工程上经常忽略不计，故认为不能直接引起土体的变形和强度变化，所以又称为中性应力[7]。因此，土体在垂直方向所受的总应力σ为有效应力σ′与孔隙水压力u之和。这就是有名的有效应力原理，当水位下降到一定深度后，土中的孔隙水压力降低，由于总压力基本不变，则有效应力相应增大，如图3、图4所示，t=10 a时，抽水井附近有效应力较大，最大为4.14×105Pa，水头最大为Hmax=-30 m。

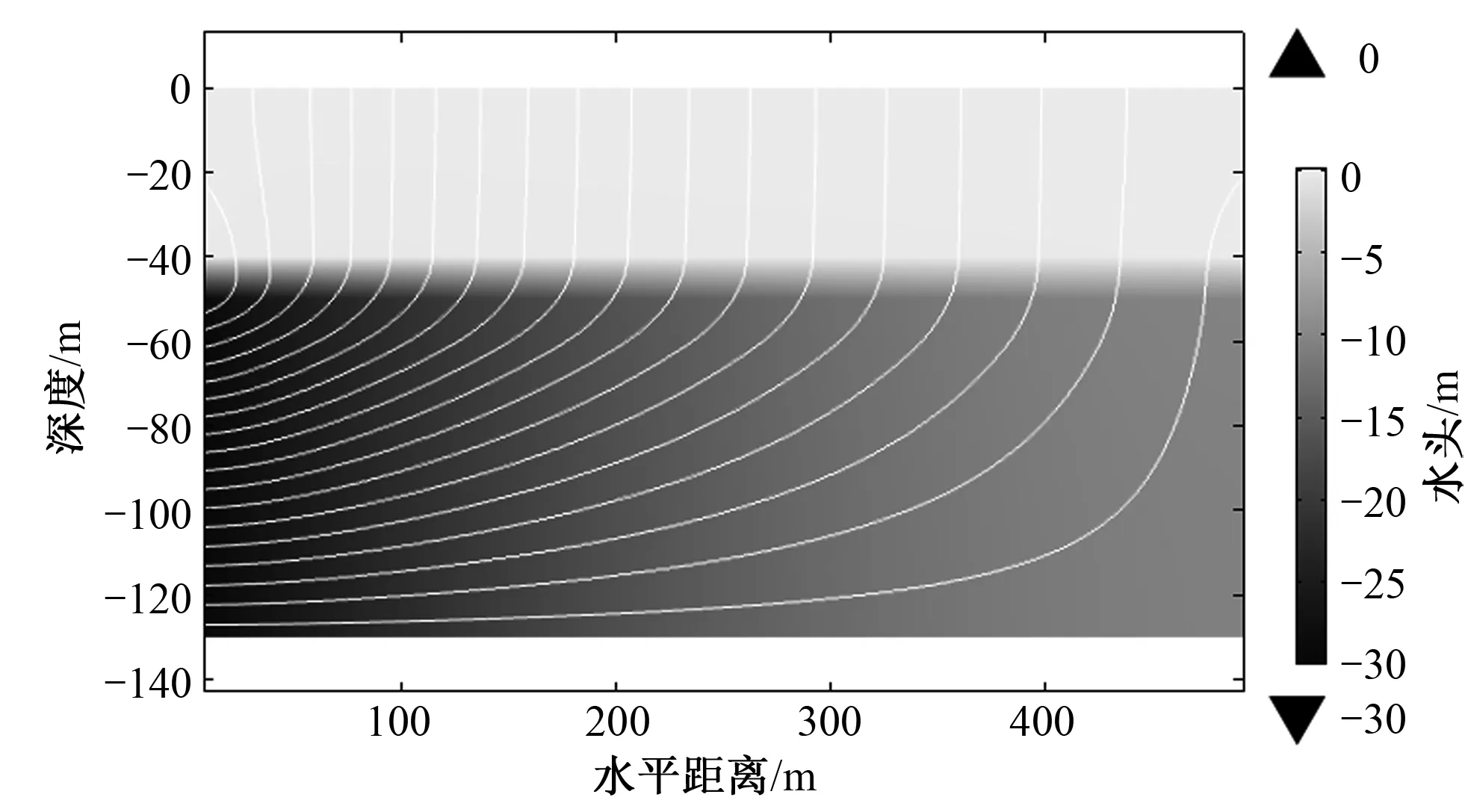
图4 t=0～10 a，流线分布与Von Mises应力云图

通过计算得到模型中各监测点近10年的地表沉降量(图5)，根据计算结果，在降水固结过程的初期，由于有效应力的增加，引起土体固结压缩，且随着时间的推移而发生，呈线性变化；靠近抽水井附近的监测点1的10年累计下沉值最大，达到1.12 m，监测点2的累计下沉值为0.72 m，监测点3的累计下沉值最小，为0.41 m；并将其分别与实际的监测结果进行拟合对比，整体效果较好，则可以认定所建的数值模型正确，参数较合理，能很好地反映研究区的沉降特征。

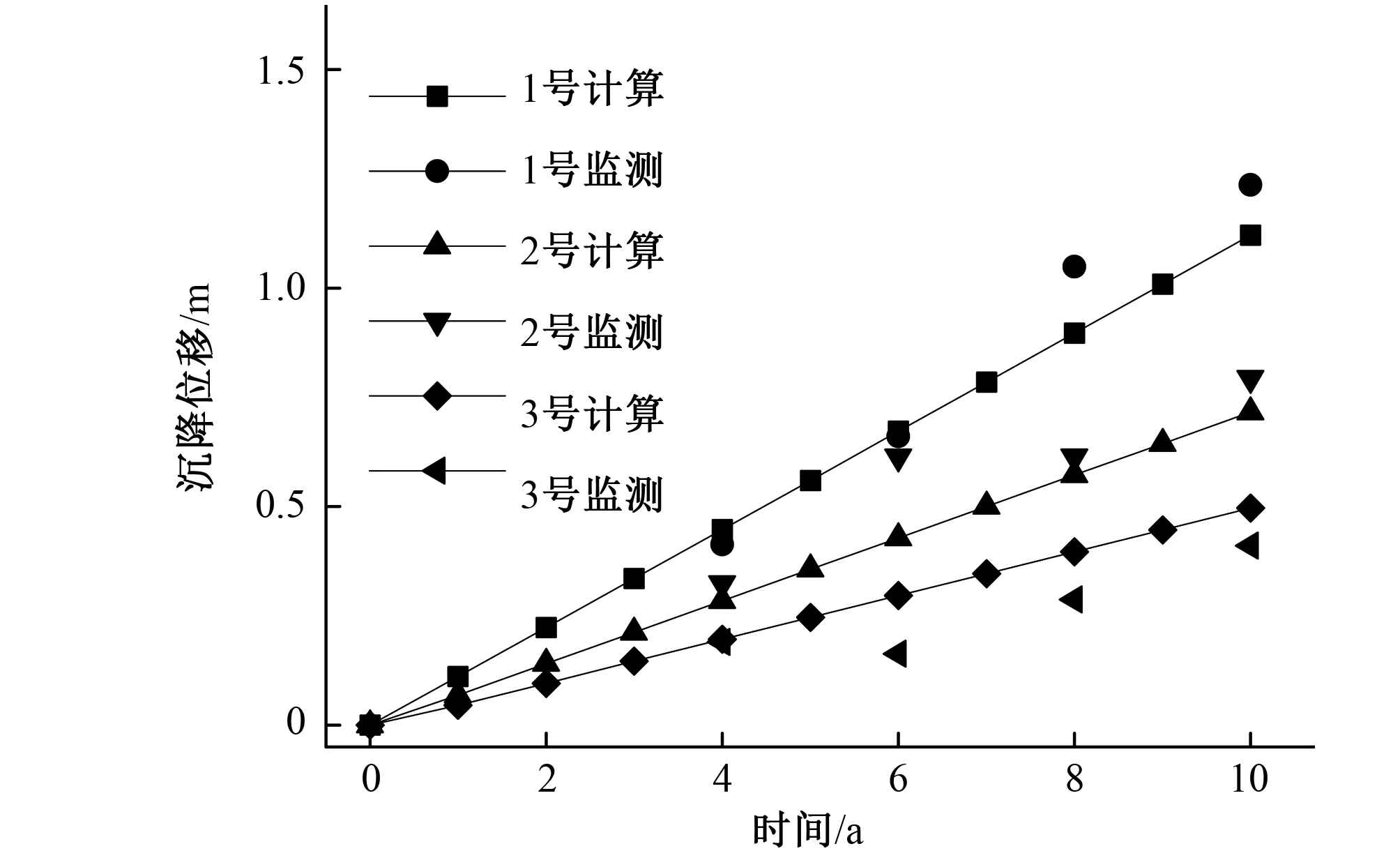
图5 t=0～10 a，水头和流速分布图

通过计算不同开采工况得到t=10 a时地表沉降量(图6)，根据计算结果，在H1=-0.5t(日出水量Q=1 400 m3)的工况条件下，地表变形较小，根据《建筑地基基础设计规范》，不会引起墙体及房屋的破坏，所以，将日开采量控制在1 400 m3以下能有效避免地面沉降造成的破坏。

3 结 论

(1)采用多物理场耦合分析软件Comsol Multiphysics中的多孔弹性物理场接口建立的地下水抽取-地面沉降流固耦合模型，实现了达西定律场和固体力学场的真耦合，能够精确反映地表变形位移以及含水层水头、土体孔隙水

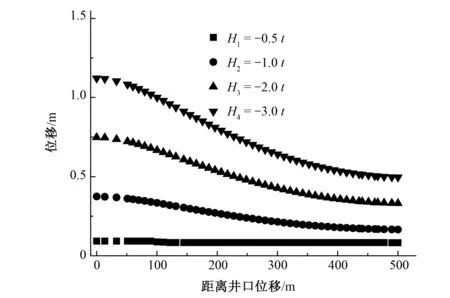
图6 研究区各监测点沉降拟合图

压力分布情况。

(2)通过分析计算，确定了地下水抽取引起的地面变形的影响范围；根据有效应力原理，当水位下降到一定深度后，土中的孔隙水压力降低，由于总压力基本不变，则有效应力相应增大，引起土体固结压缩并得出t=10 a时，抽水井附近最大效应力σ′max=4.14×105Pa，水头最大值为Hmax=-30 m。

(3)土体固结压缩随着时间的推移而发生，呈线性变化；并对位移的计算结果与监测结果进行拟合对比分析，认定所建的数值模型正确，参数较合理，能很好地反映研究区的沉降特征。

(4)通过计算不同开采工况，根据计算结果，给出最佳的沉降控制措施：将日开采量控制在1 400 m3以下，有效避免地面沉降造成的破坏。

□

[1] 纪佑军,刘建军,程林松.考虑流-固耦合的隧道开挖数值模拟[J].岩土力学,2011,32(4):1 229-1 233.

[2] 陈仕阔,杨天鸿,王 航,等.高富水砂层地铁竖井动态降水优化及固结变形预测[J].东北大学学报(自然科学版),2011,32(9):1 328-1 331.

[3] 陈 杰,朱国荣,顾阿明,等.Biot固结理论在地面沉降计算中的应用[J].水文地质工程地质,2003,30(2):28-31.

[4] 张 云,薛禹群.抽水地面沉降数学模型的研究现状与展望[J].中国地质灾害与防治学报,2002,13(2):1-6.

[5] 李元雄.李元雄.抽汲地下水引起地面沉降三维数值模拟及工程应用研究[D]. 武汉：中国地质大学,2007.

[6] 唐金颖.地下水开采引起地面沉降的数值模拟分析[D]. 沈阳：东北大学, 2008.

[7] 李志平.基坑降水引起的地面沉降分析[D]. 长沙：中南大学,2008.