基于系统熵值分析的水资源复合系统承载力可变模糊综合研究

2017-03-22薛联青陈新芳张洛晨

中国农村水利水电 2017年10期

薛联青，时佳，陈新芳，张洛晨，孙超

(1.河海大学水文水资源学院，南京 210098；2.石河子大学，新疆石河子 832003；3.新疆塔里木河流域管理局，新疆库尔勒 841000)

0 引言

水资源是社会发展的基础，与人类的生产，生活以及生态等活动都密切相关[1]。水资源大系统是由宏观经济社会-水资源-生态环境组成的复杂巨系统，各子系统间相互影响，紧密相连[2]。其中，水资源是社会经济发展和生态环境循环的物质基础，合理的开发利用能保障社会经济的稳固进步和生态环境的良性循环；经济社会进步则是人类发展目标，其间伴随着水资源的消耗，对生态环境造成一定压力，但其发展成果可以完善基础设施建设，提高技术水平，推进其他系统的发展。生态环境系统良性循环可以保证水资源复合系统的代谢更新，它在消耗资源的同时也容纳同化其他子系统产生的废物，从而促进整个复合系统可持续发展[3]。因此，关于水资源承载水平的研究，需要分析复合系统下各子系统的发展态势，协调其相关关系，达到水资源复合系统整体最优的效果。

熵值是用以表征系统混乱程度的度量，熵值越大，系统混乱程度越大，越不利于系统的良性循环[4]。本文通过计算各系统熵值大小可以衡量系统间发展的协调程度。针对水资源复合系统特性，构建水资源承载力调控模型,通过系统熵值调控，令社会经济，水资源和生态环境系统协调发展，同时得到调控后的控制参量组合，即承载力调控方案，从而达到优化水资源复合系统，提高水资源承载力的目标。

1 水资源承载力调控模型指标体系

水资源承载力是在一定的社会背景及技术支持条件下，对该地区社会可持续发展(包括工业、农业、社会、人口和生态环境等)的最大支撑能力[1]。因此，评价指标体系的建立，需要考虑体系的完整性，指标的代表性和可行性。本研究借鉴相关研究，并参照全国水资源供需分析中的指标体系从水资源，社会经济以及生态环境三方面考虑,选取了12项指标对水资源承载水平进行评价[5-9]。该指标体系可以全面描述水资源承载力的相关影响要素以及流域水资源利用特点，从而对流域水资源承载水平做出科学合理的评价。本研究将每项指标分为3个等级，其中V1代表情况良好，有很大承载潜力；V2级别表示可承载；V3级别代表超载，如不加以治理会导致环境恶化。分析指标层内容，结合实际可采取的调节手段构建调控参量体系，旨在通过调整相关参量达到优化协同各子系统发展的目标。

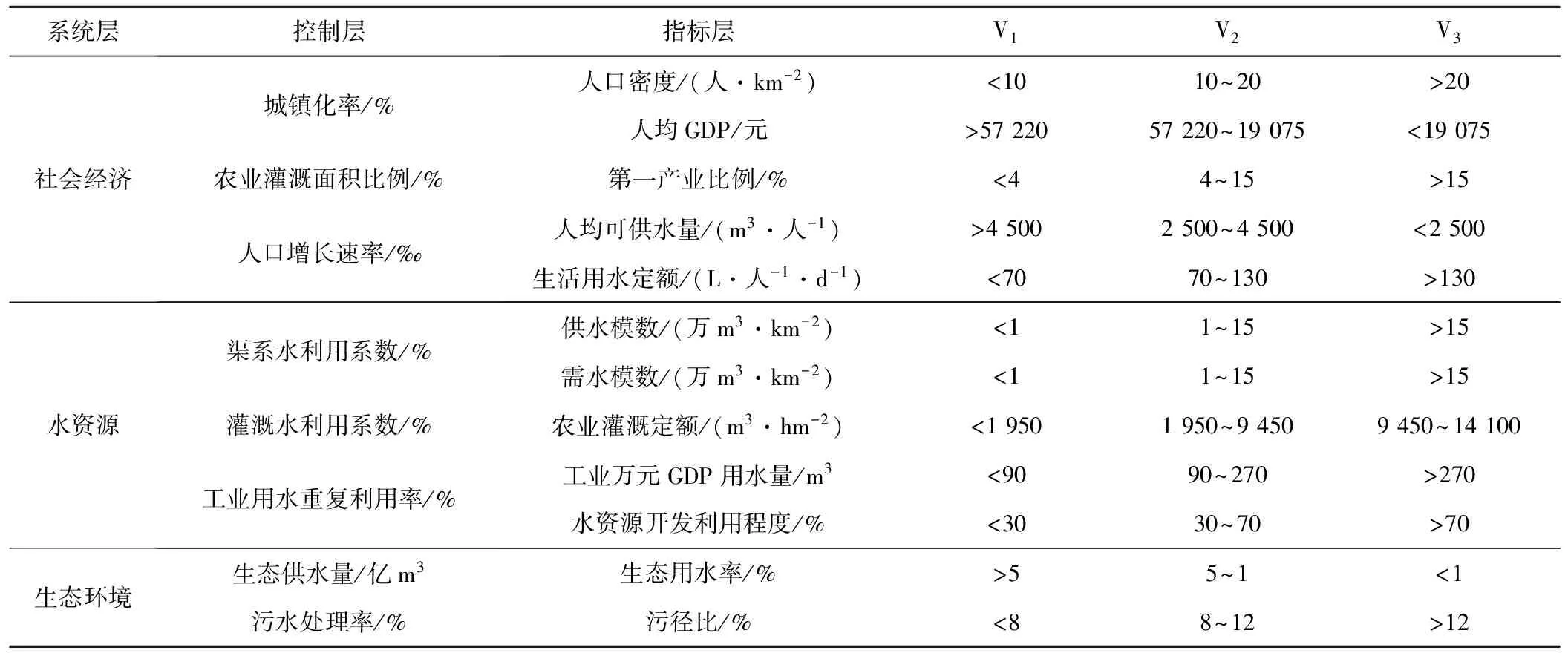
表1 水资源承载力调控评价指标体系Tab.1 Regulation index system of the water resources carrying capacity

2 水资源复合系统承载力调控模型

2.1 水资源复合系统协调程度计算

调控参量是各子系统发展效应的表征和度量，各参量间的关系变化决定着系统的演变方向，为描述系统整体行为利用调控参量构建有序度函数，用以衡量各子系统的发展协调程度[9]。设系统Xj调控参量为ej=(ej1,ej2,…,ejn)，其中效益型调控参量B，其取值越大,系统Xj有序度越高;对费用型调控参量P，则取值越小，系统的有序度越高[2]。

(1)

式中：uj(eji)为调控参量eji的有序度；βji和αji分别为eji的最小和最大临界阈值。对于效益型指标，若调控参量eji的有序度值uj(eji)∈[0,1]，则调控参量在临界阈值区间，且其值越大，eji对子系统有序度的“贡献”越大，费用型指标则相反。若u(eji)∉[0,1]，说明eji不在合理阈值区间，需进行调节。调控参量eji对水资源子系统有序程度的“总贡献”可通过uj(eji)的集成来实现：

(2)

熵值是描述系统有序程度的物理量。系统有序度越高，熵值就越低；越是无序，熵值就越高。利用熵与有序度间的关系，建立有序度熵函数，对系统演化方向进行分析：

(3)

式中：U1(E1)、U2(E2)、U3(E3)分别代表社会经济、水资源和生态环境系统的有序度。

ΔZy=Zy(n+1)-ZY(n)

(4)

当熵变ΔZY>0时，表示调控后复合系统总熵增加，系统向无序方向演化；熵变ΔZY<0，即系统靠近熵产生最小的状态，表明系统总熵减小，相对于调控前系统趋向于良性循环状态；当熵变ΔZY=0时，表明调控后熵无变化，系统熵收敛，实现寻优[10]。

2.2 系统熵值调控过程

熵值调控过程依据调控流程图进行,从初始调控方案输入开始依次决策计算。首先对比各调控参量有序度与[0，1]区间位置关系，如果有序度超出[0,1]范围,则说明调控参量不满足临界阈值要求，需要反馈信息,调节相关参量得到新的调控参量方案。依次对后序目标进行决策计算，直至调控参量和各子系统有序度均在合理范围内。如果系统有序度均满足区间限制，但相互之间差值较大，则说明各子系统发展协调性差，此时，也需要对相关调控参量进行调整[11]。最后计算水资源复合系统有序度熵值，若熵值减少，说明调控方案可行，社会经济，水资源，生态环境3个系统趋向于更协调，否则需要进一步采取调控措施，直至系统熵值减小，令决策者满意为止。

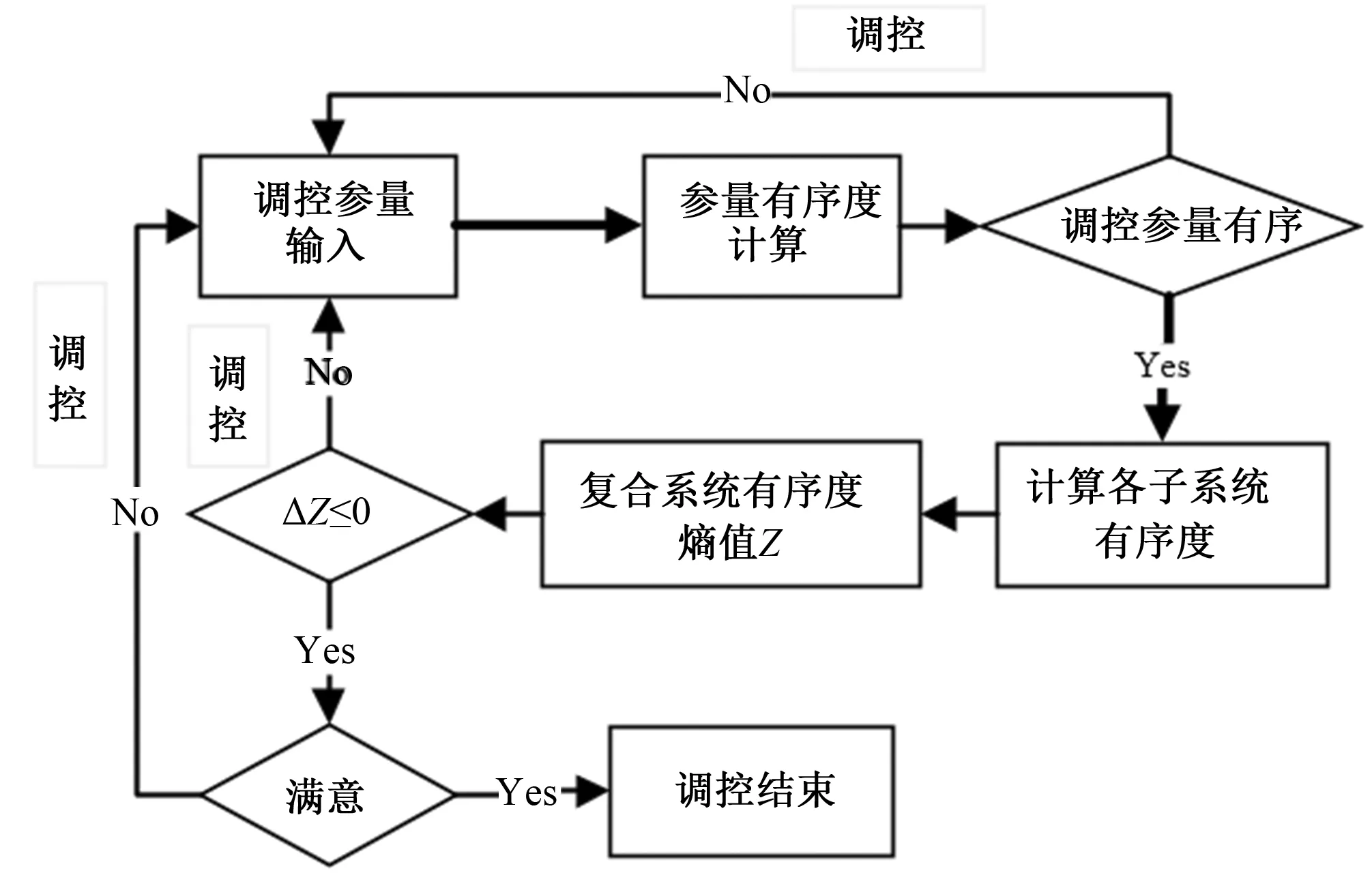
图1 系统熵值调控流程图Fig.1 The flow chart of system entropy regulation

2.3 水资源复合系统承载力计算

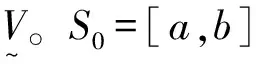
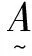
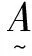
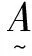
μ(u)=[1+D(u)]/2

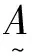
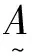
(5)

2.3.1 计算评价指标相对隶属度

利用相对差异函数模型确定指标对标准区间的隶属函数,可以避免分级计算时的级别跳跃现象，实现指标在样本相邻级别间的平稳过渡[13]。

根据流域水资源承载力评价指标计算情况构建评价指标特征值矩阵S=(sij)，承载力将依据评价指标特征值矩阵按照c个级别的指标标准特征值K进行识别，K=(kih)。其中sij为样本j指标i的特征值;i= 1,2,…,m;j= 1,2,…,n；kih为级别h指标i的标准特征值,h= 1,2,…,c。

参照指标标准值矩阵和流域实际情况确定水资源承载能力可变集合的吸引(为主)域矩阵Rab与范围域矩阵Rcd：

Rab=([aih,bih])

(6)

Rcd=([cih,dih])

(7)

设M为吸引域区间[a，b]中D(u)=1的点值，根据水资源承载能力分为3个级别的实际情况确定吸引(为主)域[aih,bib]中D(sij)h=1的点值Mih的矩阵。

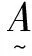
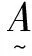
s为S区间内的任意点的量值，当s落入M点左侧时的相对差异函数模型可为：

(8)

s落入M点右侧时，其相对差异函数模型为：

(9)

式中：θ为非负指数，通常可取θ=1，即相对差异函数模型为线性函数。

式(8)～式(9)满足：①当s=a、s=b时，D(u)=0；②当s=M时，D(u)=1；③当s=c、s=d时，D(u)=-1。当s不落在区间[c，d]时，D(u)=-1，D(u)=0。

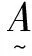
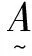
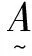
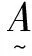
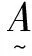
判断样本特征值sij在相应吸引域中与范围域矩阵以及Mih的位置关系，根据式(8)～式(9)计算差异度D(xij)h，由式(7)得到计算指标对h级的相对隶属度μ(xij)h。从而得到当j=1，2，3时对级别h=1，2，3的指标相对隶属度矩阵。

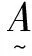
2.3.2 水资源承载力分级与计算

应用可变模糊综合评价模型计算指标样本对各级别的综合相对隶属度。

(10)

式中：U′h为样本关于级别h的非归一化综合相对隶属度；σi为权重系数；p为距离参数；α为优化准则参数。

将U′h进行归一化处理得到综合相对隶属度矩阵U=(uh)其中：

(11)

本研究将承载力分为3个级别，应用下式对样本进行分值计算与级别评价。其中， 3级(1.5～3分)代表流域水资源承载情况良好，还有很大开采空间；2级(0.5～1.5分)代表流域水资源开发利用已有一定规模，但仍具有开发潜力；1级(0～0.5分)则代表流域水资源承载情况已接近饱和状态，继续发展下去必将引发资源短缺，环境恶化等一系列失衡现象。

H=3-(1,2,3)·U

(12)

3 实例分析与计算

3.1 研究区概况

叶尔羌河流域位于新疆维吾尔自治区的西南部，地处东经74°28′～80°54′，北纬34°50′～40°31′范围。该流域发源于喀喇昆仑山脉，包含叶尔羌河、提孜那甫河、柯克亚河与乌鲁克河四条主要河流。叶尔羌河是新疆第四大河流，河流全长1 281 km，净流量76.85 亿m3，多年平均降水量仅有39.4～53.2 mm，年蒸发量则达到2 108～2 480 mm，是我国典型干旱区。流域总面积为8.58 万km2，平原区面积占33.1%，2.84 万km2。叶尔羌河流域跨4个地州12个县(市)，含县级以上用水单位共24个[14]。目前，该流域水资源开发主要用于农业生产，工业基础薄弱，商品化率较低。2013年，流域国民生产总值287.05亿元，人口达到231.72 万人,人均GDP仅1.24万元，不足全国平均水平的1/3。随着社会经济的发展，人口持续增加，耕地不断扩大，叶尔羌河向塔里木河干流输水量逐年减少，甚至断流。流域下游两岸植被大面积衰败死亡，生态环境日益恶化。社会经济系统和生态环境系统的发展失衡导致了水资源不合理的开发利用，水资源供需矛盾已经成为制约叶尔羌河流域发展的重要因素。

3.2 叶河流域水资源复合系统熵值调控

参照《喀什地区国民经济和社会发展第十二个五年规划纲要》并结合叶尔羌河流域情况，设置调控参量调控范围。其中，人口增长率最高阈值为现状年计算值，最低阈值为规划数值；对于生态用水率，最低阈值为河道内生态基流需水量，最高阈值为满足河道内外生态需水水量。其余指标最高阈值为规划数值，最低阈值为流域内最低水平数值。

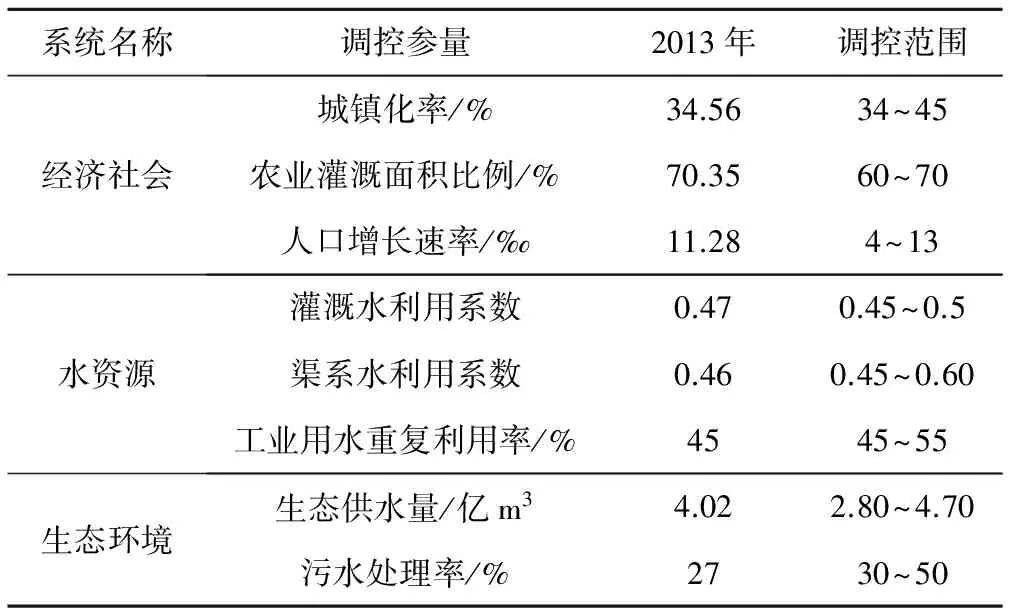
表2 水资源复合系统调控参量Tab.2 The regulation parameter of water resources complex system

将初始调控参量输入调控模型，得到3个子系统的熵值分别为0.98， 0.46和0.25，各子系统间熵差均大于0.2，尤其是经济社会系统，与其他子系统发展极不协调，不利于复合系统的良性循环。判断各调控参量调整方向，以一定步长进行调整，具体调节过程如下(见图2)。经过12次调控，各调控参量依次为40.05、69.50、11.27、0.48、0.54、52、4.43，41，此时复合系统熵有明显降低且收敛，叠代熵变△Z≤0.005，符合调控收敛标准，系统收敛熵为0.277 0。由此，系统熵值调控过程可以科学合理的控制系统发展速度，协调生态环境、经济社会和水资源三者之间的关系，使各子系统间熵值差△U≤0.2，实现复合系统的优化发展。

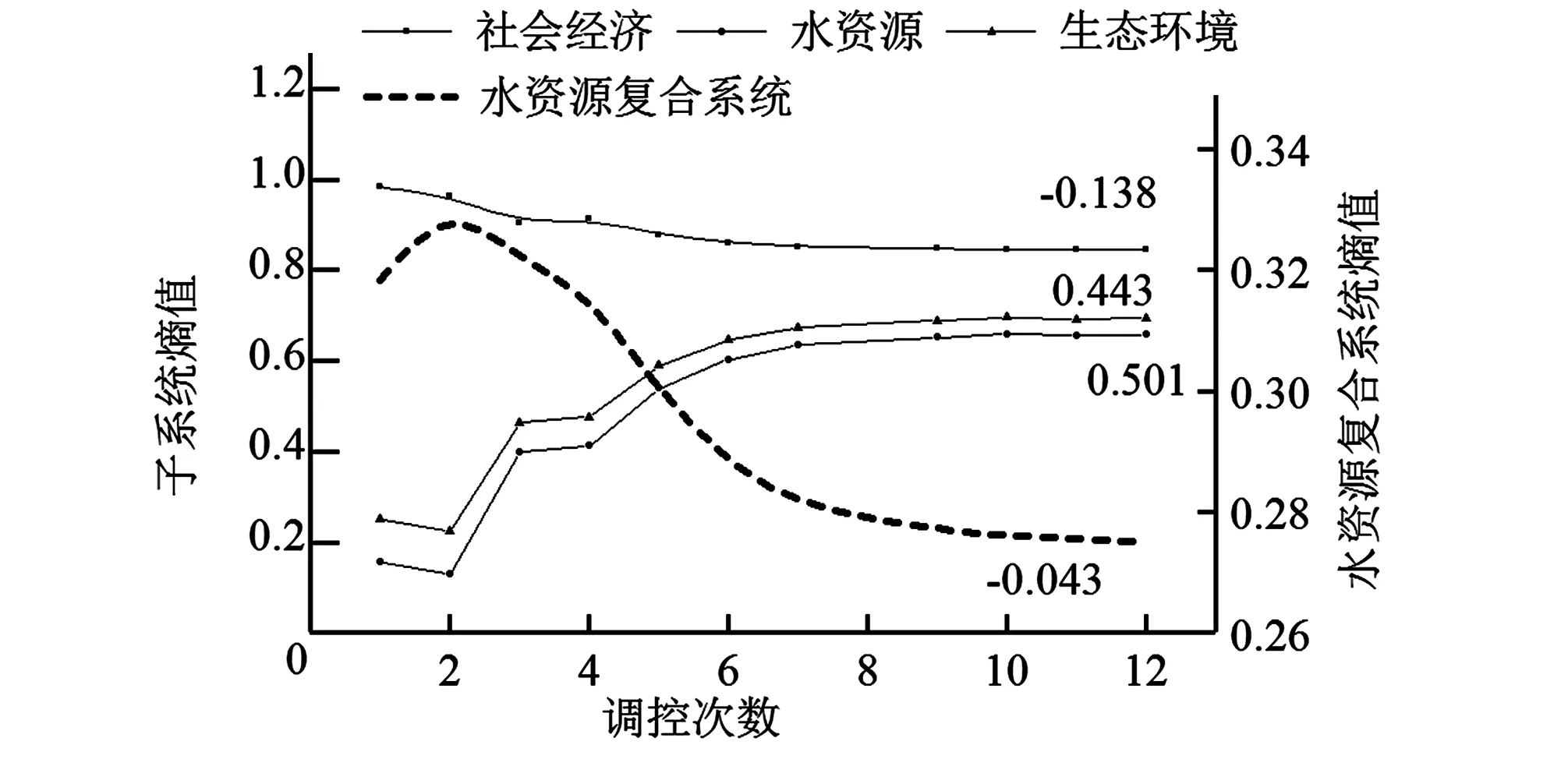
图2 系统熵值变化图Fig.2 The system entropy variation

3.3 多情景模拟

为探究系统协同发展对于水资源承载能力的重要意义，设置多个模拟方案对叶尔羌河流域水资源承载力进行评价，以验证模型的先进性与实用性。

情景1：模拟叶尔羌河流域2020年系统状态，各调控参量均维持现状年2013年数值。

情景2：单系统调控，在情景1的基础上，考虑社会经济系统调控。

情景3：单系统调控，在情景1的基础上，考虑水资源系统调控。

情景4：单系统调控，在情景1的基础上，考虑生态环境系统调控。

情景5：复合系统调控，在情景1的基础上，考虑社会经济，水资源，生态环境系统的协同调控。

3.4 水资源承载力评价

将指标计算结果代入承载力评价计算模型，利用熵权法计算指标权重依次为0.048，0.092，0.072，0.068，0.058，0.081，0.057，0.091，0.106，0.159，0.108，0.061。通过可变模糊综合计算得到各情景下叶尔羌河流域水资源承载力得分及分级情况。

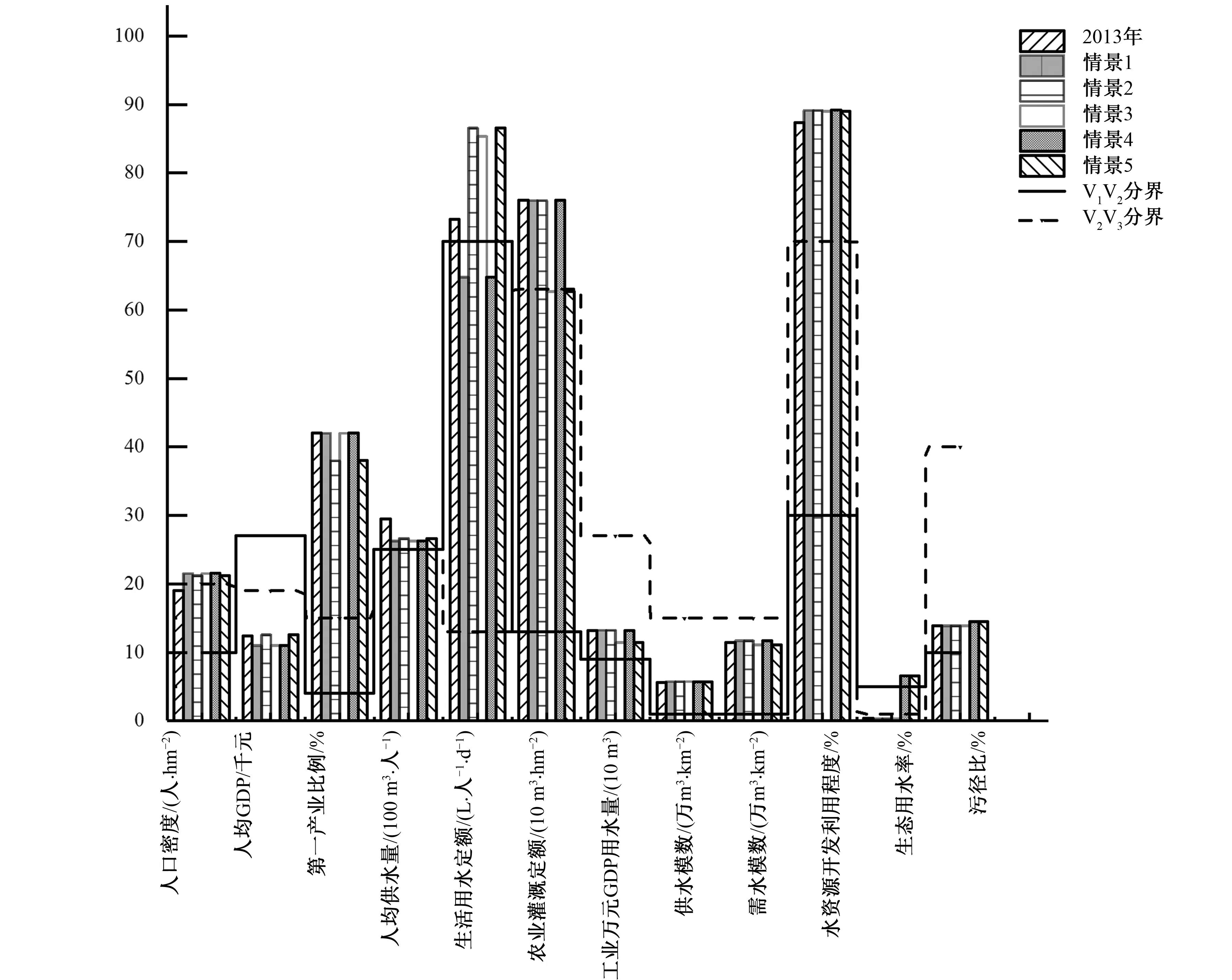
图3 各情景下评价指标计算情况Fig.3 The evaluation index calculation of each scenario

名称2013年情景1情景2情景3情景4情景5分值0．51～0．730．36～0．600．47～0．710．48～0．720．47～0．740．69～0．88级别21～21～21～21～22

由评价结果可知，叶尔羌河流域现状年水资源承载力处于2级初始阶段，社会经济-水资源-生态环境系统发展失调，若按此趋势继续发展，2020年承载力将接近饱和状态，即情景1。经过系统协同调控后，各子系统优化有序，发展均衡，承载力上升至2级中段，分值为0.69～0.88，较现状年有明显升高。若仅对单独子系统进行优化，分别得到情景2、3、4，其评价结果均处于1～2级，虽然较情景1分值有所上升，但效果不明显，由此可见系统协调发展对水资源承载力的重要意义。

4 结果与讨论

(1)利用水资源承载力调控评价模型对该流域的社会经济-水资源-生态环境系统间的协同性做出评测，结果表明，现状年该流域各子系统发展严重失衡，水资源承载力也处于2级初始阶段，接近饱和状态。对该流域调控参量进行调控，优化协同各子系统，使复合系统熵值稳定收敛，达到良性循环效果，同时可变模糊综合评价分值上升，流域水资源承载力提高。

(2)为验证系统协调发展对水资源承载力提高的重要性，设置情景2、3、4、5进行模拟评价，结果表明，单独子系统的优化对承载力提高的效果甚微，而各子系统相互协调，发展均衡，可以使水资源承载力有显著提高。

(3)根据系统调控前后调控参量对比，部分调控参量调节幅度较大，第一产业比例下调10.1%，人口增长速率降低12%，渠系水利用系数提高了17.1%可以发现，污水处理率提高52.2%。由此可见调整产业结构，降低人口增长速度，建立高效节水农业体系，提高污水处理技术等系列措施可以有效协调叶尔羌河流域各子系统发展，做到由耗水型经济结构向节水型经济结构转变，以提高流域的水资源复合系统承载能力。

[1] 夏军.水资源安全的度量：水资源承载力的研究与挑战(一)[J]. 海河水利,2002,(2)：5-7.

[2] 王浩, 王建华, 秦大庸. 流域水资源合理配置的研究进展与发展方向[J]. 水科学进展, 2004,15(1):123-128.

[3] 马向东, 孙金华, 胡震云. 生态环境与社会经济复合系统的协同进化[J]. 水科学进展, 2009,20(4):566-571.

[4] 陈玉娟, 查奇芬, 黎晓兰. 熵值法在城市可持续发展水平评价中的应用[J]. 江苏大学学报(社会科学版), 2006,8(3):88-92.

[5] 李丽琴, 谢新民, 韩剑桥,等. 面向可持续发展的水资源优化配置研究[J]. 中国农村水利水电, 2013,(1):15-18.

[6] 段春青,刘昌明,陈晓楠,等.区域水资源承载力概念及研究方法的探讨[J].地理学报,2010,65(1):82-90.

[7] 许有鹏. 干旱区水资源承载能力综合评价研究----以新疆和田河流域为例[J]. 自然资源学报, 1993,8(3):229-237.

[8] 黄永基,马滇珍.区域水资源供需分析方法[M].南京：河海大学出版社,1990：244-257.

[9] 陈亚宁．新疆塔里木河流域生态水文问题研究[M]．北京：科学出版社,2010：390-392.

[10] 陈效国. 黄河流域水资源演变的多维临界调控模式[M]. 郑州：黄河水利出版社, 2007:105-109.

[11] 彭少明,信劲松,黄强,等. 黄河流域水资源多维临界调控理论与模型研究[J]. 水利水电科技进展,2005,(1):9-11,50.

[12] 陈守煜.工程可变模糊集理论与模型----模糊水文水资源学数学基础[J].大连理工大学学报,2005,(2):308-312.