双轴惯导轴系非正交误差全空间补偿技术研究

曹 文

(华中光电技术研究所 武汉光电国家实验室，武汉 430223)

双轴惯导轴系非正交误差全空间补偿技术研究

曹 文

(华中光电技术研究所 武汉光电国家实验室，武汉 430223)

旋转调制技术实现了捷联惯导的高精度长航时导航，但轴系非正交误差的存在影响着导航姿态精度。传统轴系非正交误差补偿方法是针对旋转轴停留在固定位置完成的，提出一种全空间的轴系非正交误差补偿方法，不限定旋转轴的转停位置。试验结果证明该误差补偿方法较传统方法更优，对惯导姿态精度提升明显。

惯性导航系统；双轴旋转调制；轴系非正交误差；全方位补偿

0 引言

旋转调制是一种系统级误差补偿方案，通过转位机构拖动IMU以某个坐标系旋转，从而使其误差在此坐标系下被调制成均值为零的周期变化量，在惯性元件本身输出精度没有改善的情况下提高系统长航时的导航精度。单轴旋转不能调制旋转轴方向上惯性器件常值误差引起的导航误差，标度因数非线性误差也会引入一个量级较大的导航误差，致使导航精度受到限制；双轴旋转能够抵消掉所有惯性器件常值漂移引起的导航误差，是旋转惯导系统发展的必然趋势。国外采用该技术的MK49及AN/WSN-7A系列激光捷联惯导系统早已成熟应用于水面舰船及潜艇中[1-4]。然而，由于机械零部件的精度和安装工艺的限制，双轴旋转调制惯导系统的内外环旋转轴存在不严格正交，这会造成IMU(惯性测量单元)存在轴系安装误差，本文提出一种双轴惯导轴系非正交误差全空间各个方位下的补偿方法，运用该方法可以实现对轴系非正交误差的全方位计算估计，实现任意角度的非正交误差补偿。

1 双轴非正交误差分析

旋转调制的机理就是通过周期性旋转将系统主要误差源调制成周期信号形式，从而在积分解算中得到均化，提高系统精度。受限于调制旋转轴系的加工精度及安装工艺，旋转轴存在的不严格正交导致旋转调制停在不同位置时的载体姿态输出存在幅值很大的方波误差[5-7]。当进行旋转调制时，IMU通过旋转机构固连于载体，定义旋转坐标系p，此时IMU正交安装误差是IMU坐标系相对于p系的误差，初始时刻p系与b系重合。陀螺仪和加速度计的输出为沿旋转坐标系p系的分量，在进行导航解算时需先将其投影到载体坐标系中。定义b系为载体坐标系、s系为惯性测量组件坐标系，则系统航姿调制解调时，惯性测量组件相对载体间的姿态转移矩阵可表示为

(1)

对式(1)进行变换，可将载体运动表示为

(2)

为简化分析，假设载体处于静止状态，k时刻转台测角为0，k+1时刻转台测角为α，则

(3)

2 误差数学模型建立

目前对轴系非正交误差的补偿一般是针对特定调制策略实现[8-10]，即当旋转轴转停到固定位置时，对固定位置下的转轴坐标系的非正交性进行补偿，一旦转停位置发生变化时或采用基于地理系调制的转位控制方案时，转位机构可能停留在空间的任意位置，这种补偿方法将不能达到补偿效果。通过建立2个旋转轴360°全角度的运动模型，对轴系非正交误差进行全方位的计算估计，可实现任意角度的非正交误差补偿。以方位轴转动情况为例，假设转轴在各个位置的轴晃是均匀的，即将转动过程近似认为转轴绕某一固定轴线方向做圆锥运动，圆锥角为γ,如图1所示。

图1 方位轴圆锥运动示意图Fig.1 Coning motion of azimuth axis

图1中，Zs表示惯性测量组件坐标系Z轴指向，Zr′表示转轴坐标系Z轴指向，Zr表示转台实际转动轴指向。以u表示Zs轴向单位向量，略去二阶小量，则u在Zr轴向的投影可表示为

(4)

(5)

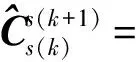
(6)

将式(6)代入式(2)可得

(7)

则姿态误差可表示为：

φx=arcsin(T32)=arcsin[2(q2q3+q0q1)]

(8)

由式(5)、式(8)即可得出方位轴转动时，系统航姿调制解调误差与轴系非正交性误差及转台测角间的关系。

为便于工程实际应用，将惯性测量组件安装轴向指向误差及轴系晃动误差统一为待标定系统，对上述各姿态误差数学模型进行统一简化为：

φx=kx0+kx1sinα+kx2cosα+kx3sin2α+kx4cos2α

φy=ky0+ky1sinα+ky2cosα+ky3sin2α+ky4cos2α

φz=kz0+kz1sinα+kz2cosα+kz3sin2α+kz4cos2α

(9)

俯仰轴转动分析过程与此类似。

3 仿真试验

3.1 旋转路径设计

基于上述数学模型，为有效分离标定式(9)各项系数，设计旋转路径如下：

1)次序1：惯性测量组件绕内环轴正向转动360°；

2)次序2：惯性测量组件绕内环轴反向转动360°；

3)次序3：惯性测量组件绕外环轴正向转动360°；

4)次序4：惯性测量组件绕外环轴反向转动360°。

利用上述4次序转动方案，结合主惯导输出同步航向、姿态信息，即可完成上述数学模型相关系数的在线自动标定。

3.2 结果与分析

内环0°，外环以1(°)/s的速度正转1周、反转1周，轴系非正交性误差情况：其中，红色、蓝色虚线分别表示转台内外环测角，粉色表示姿态误差，如图2～图4所示可以看出，外环转动1周，航向、纵摇误差波动峰峰值均在25″内，横摇误差波动峰峰值在45″左右。

图2 补偿前航向误差示意图Fig.2 Heading error before compensating

图3 补偿前纵摇误差示意图Fig.3 Pitch error before compensating

图4 补偿前横摇误差示意图Fig.4 Roll error before compensating

采用多项式拟合为

δθ=a+b×sinA+c×cosA+

d×sin2A+e×cos2A

拟合结果为

dH_A1_0= 3.346 -3.006*sA1 -0.16*cA1+

5.737*sA12 -4.572*cA12

dP_A1_0= -4.596 -2.513*sA1 +0.467*cA1+

4.695*sA12 +5.998*cA12

dR_A1_0= 2.083 -15.24*sA1 -1.084*cA1+

5.212*sA12 +0.205*cA12

补偿后结果：其中，红色、蓝色虚线分别表示转台内外环测角，粉色表示姿态误差, 红色点线表示外环测角拟合补偿后的剩余残差，如图5～图7所示，可以看出，经补偿后，航向、纵摇误差波动峰峰值均在8″左右，横摇误差波动峰峰值在15″左右。

外环0°，内环以1(°)/s的速度正转1周、反转1周，轴系非正交性误差试验情况类似，如表1所示。

图5 航向补偿后误差示意图Fig.5 Heading error after compensating

针对固定位置补偿以及全方位补偿后16次序转动的误差情况统计(在3倍标准差范围内)如下：补偿方法航向误差/(″)纵摇误差/(″)横摇误差/(″)固定位置补偿10897651381全方位补偿898401605

从统计结果可以看出，航向误差减小20%，纵、横摇误差减小50%。

4 结论

本文针对提高双轴调制惯导导航精度，对轴系非正交误差的补偿需求，提出了全方位的轴系非正交误差的补偿技术，该技术与传统固定位置补偿方法相比有较大提升。该方法针对轴系的运动过程建立了运动数学模型，经过试验验证，模型通用性较强、补偿效果较好。

[1] Lahham J I, Wigent D J, Coleman A L. Tuned support structure for structure-borne noise reduction of inertial navigator with dithered ring laser gyros(RLG)[C]. IEEE Position Location and Navigation Symposium， 2000: 419-428.

[2] Levinson E, Majure R.Accuracy enhancement techniques applied to the marine ring laser inertial navigation(MARIN)[C].Institute of Navigation Nation Technical Meeting, Anaheim, CA, 1987.

[3] MK39 MOD. 3A ring laser ship’s inertial navigation system[J]. Morthrop Grumman Electronic Systems-Sperry Marine. Printed in U.S.A, 2005: 4-6.

[4] 王宇. 机抖激光陀螺捷联惯性导航系统的初步探索[D]. 长沙：国防科学技术大学, 2005.

[5] 翁海娜，陆全聪，黄昆，等. 旋转式光学陀螺捷联惯导系统的旋转方案设计[J]. 中国惯性技术学报，2009, 17(1)： 8-14.

[6] 陆志东，王晓斌. 系统级双轴旋转调制捷联惯导误差分析及标校[J]. 中国惯性技术学报，2010, 18(2)： 135-141.

[7] 王子磊，尹洪亮，王丹. 激光陀螺双轴旋转惯导系统转位方案设计[J]. 舰船科学技术， 2013， 35(12)： 114-120.

[8] 曹文，周平璜. 双轴调制惯导自动补偿轴系非正交误差的方法[J]. 光学与光电技术, 2015： 31-35.

[9] 高钟毓. 惯性导航系统技术[M].北京:清华大学出版社,2012.

[10] 袁保伦. 四频激光陀螺旋转式惯导系统研究[D].长沙:国防科学技术大学,2007.

Research on Omnibearing Compensation Method of Nonorthogonal Errors for Dual-axis INS

CAO Wen

(Huazhong Institute of Electro-Optics,Wuhan National Laboratory for Optoelectronics, Wuhan 430223,China)

Based on the theory of rotation modulation technology, the inertial navigation system (INS) can perform high precision long-endurance navigation, howerver the existance of nonorthogonal errors brings negative effects on improving navigation accuracy. Compared to the classical method of compensation which is performed when the axis is controlled staying in some fixed directions , the omnibearing direction compensation method proposed here can be applied without limiting the pausing position of the axis. The experiment results indicate that the new method is more effective than the classical one.

Inertial navigation system; Dual-axis rotational modulation; Nonorthogonal errors; Omnibearing compensation

10.19306/j.cnki.2095-8110.2017.01.006

2016-11-15；

2016-12-30。

海军“十三五”预先研究项目(302017010203)

曹文( 1981-) ，男，硕士，工程师，主要研究方向为潜艇双轴激光惯导系统。E-mail：13638600805@139.com

U666.12

A

2095-8110(2017)01-0032-04