结构参数对弹上电子设备双层减振系统减振性能的影响规律研究

姚建军,向伟荣,闫红松,甄 瑞,余盛强

(北京自动化控制设备研究所,北京 100074)

结构参数对弹上电子设备双层减振系统减振性能的影响规律研究

姚建军,向伟荣,闫红松,甄 瑞,余盛强

(北京自动化控制设备研究所,北京 100074)

针对弹上电子设备双层减振系统结构参数设计问题,研究了一二级减振系统的频率比、质量比、阻尼比对双层减振系统在随机振动激励下的绝对加速度响应峰值、全频段的加速度响应均方根值、高频段的加速度响应均方根值、相对位移响应均方根值、耦合频率等动力学参数的影响规律,得出一般性的结论,并探讨了双层减振技术的应用,可为弹上电子设备双层减振系统的减振性能设计提供理论支撑。

双层减振;随机振动;响应特性

0 引言

导弹等航天器在空中飞行的过程中,由于边界紊流等的影响而受到强烈的随机振动激励。振动造成弹上电子设备性能下降或电子元器件损坏而影响正常工作。减振设计历来是弹上电子设备环境适应性设计的重点和难点。在电子设备对振动环境不太敏感或环境条件不太恶劣的情况下,对设备整体或设备内部的易损部件通过减振器进行单层减振通常是可行的。但当设备对振动环境特别敏感或者振动环境特别恶劣而使单层减振难以满足要求的情况下,人们便把目光投向双层减振。所谓双层减振,就是将设备或设备内部的部件通过减振器等装置柔性地联结到已经经过一级减振的基础结构上进行二次减振,其力学模型如图1所示。此外,将单层减振系统安装在刚度比较小的基础结构上时,可看作是双层减振的一种特殊形式。

对于双层减振系统理论模型及其响应特性的研究是振动力学的经典内容[1-2]。但其研究的激励条件是单频简谐振动,研究的重点是寻求使一级被减振部件位移响应最小的二级减振元件参数的最优配置。后来,随着应用的需要,有学者开始讨论宽带随机振动激励条件下，使一级被减振部件位移响应均方值最小的二级减振元件参数的最优配置问题[3],讨论在随机振动激励条件下,一、二级被减振部件的位移响应均方值与激励条件均方值之比以及加速度响应均方值与激励条件均方值之比随两级减振器参数配置的变化规律等问题[4-5]。这些工作对开展弹上电子设备的双层减振设计具有一定的参考价值,但也有诸多不足之处。首先,在实际工程中,由于种种条件的限制,设计参数难以实现最优取值,通常的做法是根据设计参数对设计目标的影响规律来折中确定较佳方案。其次,在讨论两级减振参数的配置对响应特性的影响时,由于参数变动范围较小或取值范围偏离现实情况、用来表征响应特性的参数选择不恰当等原因,得出的结论不全面且带有较大的局限性,难以满足弹上电子设备双层减振设计的需要。本文结合弹上电子设备双层减振设计的工程实际,在纠正和弥补这些不足的基础上,对两级减振器参数配置对弹上电子设备振动性能的影响规律进行了更全面、更深入的探讨,为弹上电子设备的减振设计提供理论支撑。

1 分析模型的建立

则系统的运动微分方程可写成

(1)

设系统的稳态解为

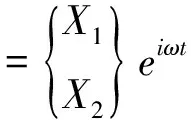
(2)

(3)

由此解得基础加速度输入对两级被减振部件绝对加速度响应的频响函数(见式(4))和基础加速度输入对两级被减振部件相对位移响应的频响函数(见式(5))

(4)

(5)

式中,

根据随机振动理论,对于只有一个输入的振动系统,其输出量的谱密度与输入量的谱密度之间的关系可用式(6)来表示。

(6)

式中:Sx(ω)为输出量的谱密度;Su(ω)为输入量的谱密度;H(ω)为输出对输入的频响函数。

响应的均方值可根据式(7)来计算。

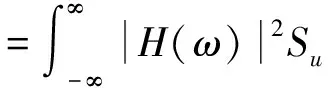
(7)

在式(1)中,令输入为零,忽略阻尼的影响,得到双层减振系统的特征方程

(8)

求解式(8)得到2个特征值,即为双层减振系统的二阶无阻尼固有频率

(9)

由式(4)、式(5)及式(9)可以发现,双层减振系统的固有特性和随机振动响应特性与两级减振系统参数的配置有非常密切的关系。

2 宽带随机振动响应特性分析

2.1 设计参数及其变动范围的确定

输入激励条件以弹上电子设备力学环境试验通常使用的加速度功率谱的形式给出,谱形如图2所示,1～1000Hz为平直段,1000～2000Hz以-6dB/oct下降。平直段谱值为方便计取1g/Hz。

图2 随机振动激励曲线Fig.2 Random vibration exciting curve

一级减振系统的设计参数原则上可以任意取值,这里给出一组具有工程原型的取值:m1+m2=10kg、f01=100Hz、ζ01=0.125或ζ01=0.05。μ、λ的取值范围在满足当前工程实际情况的基础上适当扩大,以便使所得结论更通用,取0.01～10。在研究μ和λ对双层减振系统响应特性的影响规律时,分两种状态进行讨论。第一种状态令ζ01=0.125、ζ02=0.125,此即双层减振的一般形式;第二种状态令ζ01=0.05、ζ02=0.125,此即在柔性支撑结构上安装减振系统的情形,是双层减振的特殊形式。

在研究γ对减振系统响应特性的影响规律时,先针对双层减振的一般形式,分三种状态进行讨论,第一种状态是令ζ01=0.125、ζ02=0.125(此即前述第一种状态),第二种状态是令ζ01=0.125、ζ02=0.05,第三种状态是令ζ01=0.125、ζ02=0.25。为叙述方便,这里的第二种状态和第三种状态延续前面的排序,分别称作第三种状态、第四种状态。由此初步分析阻尼比对减振系统响应特性的影响规律,在此基础上,针对受阻尼影响最为显著的设计状态,详细研究阻尼比的影响规律。

2.2 响应特性参数的确定

此外,为了分析振动过程中减振器两侧的结构件之间是否发生碰撞或出于其他考虑,通常也要关注减振器的位移均方根值。定义σ01(d)、σ02(d)分别为一级被减振部件相对基础的位移均方根值、二级被减振部件相对一级被减振部件的位移均方根值,作为响应特性参数。

2.3 质量比和频率比对响应特性的影响规律

图3～图12所示分别为第一种状态下(ζ01=0.125、ζ02=0.125),双层减振系统的各响应特性参数p1(a)、p2(a)、p1(σ)、p2(σ)、p1(σH)、p2(σH)、σ01(d)、σ02(d)、p1(ω)、p2(ω)随μ和λ的变化曲线。图13～图20所示分别为第二种状态下(ζ01=0.05、ζ02=0.125),双层减振系统的各响应特性参数p1(a)、p2(a)、p1(σ)、p2(σ)、p1(σH)、p2(σH)、σ01(d)、σ02(d)随μ和λ的变化曲线。这里需要说明的是,由于在工程上通常采用的阻尼范围内(ζ<0.3),阻尼对减振系统频率的影响较小(小于10%),故只在第一种状态下给出了频率比的变化曲线,其他几种状态与之基本一致。

由图3、图4与图13、图14可以看出,不论一二级减振系统的频率比λ、质量比μ怎么配置,一级被减振部件上的加速度响应峰值总是被降低、二级被减振部件上的加速度响应峰值总是被提高;一级被减振部件上的加速度响应峰值在λ<1时随λ的增大而降低,在λ≤1之前达到极小值,之后随λ的增大而升高,并且这种变化规律还受到μ的影响,μ越大受λ影响的区间越大、降低的幅度越大,并在μ≈1时达到极大值;二级被减振部件上的加速度响应峰值在λ<1时随λ的增大而升高,在λ≈1时达到极大值,之后随λ的增大而降低,并且这种变化规律还受到μ的影响,μ越小升高的幅度越大,甚至远远超过单层减振时的情形;在μ<1并且λ<0.1或λ>4时,一级被减振部件上的加速度响应峰值基本不受二级减振的影响;二级被减振部件上的加速度响应峰值在λ<0.2或μ>1时基本不受一级减振的影响,在λ>4时表现为一级减振系统的响应峰值,此时二级减振系统相对一级减振系统可以看作是刚体。

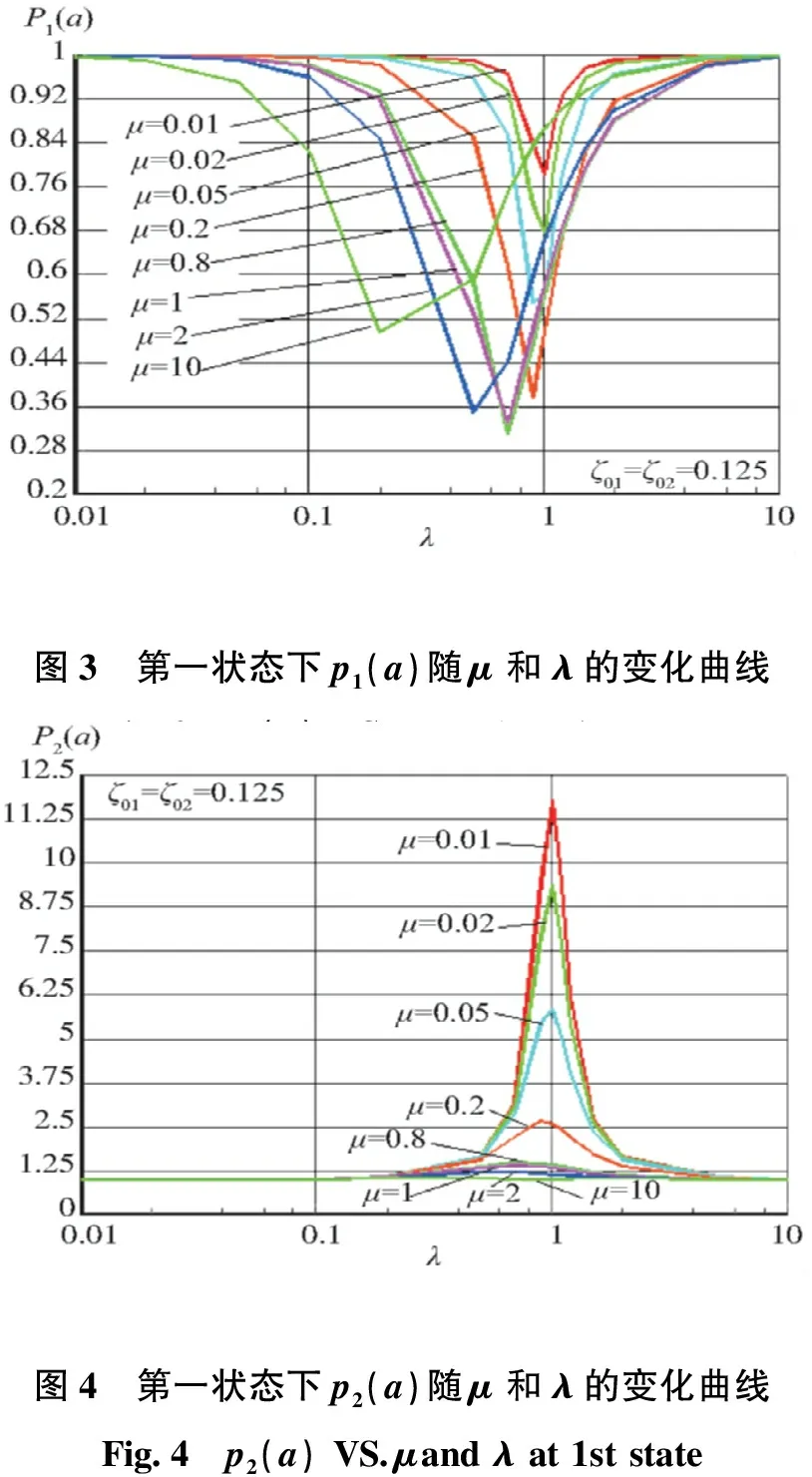
图3 第一状态下p1(a)随μ和λ的变化曲线Fig3 p1(a)VSμandλat1ststate图4 第一状态下p2(a)随μ和λ的变化曲线Fig4 p2(a)VSμandλat1ststate

图5 第一状态下p1(σ)随μ和λ的变化曲线Fig5 p1(σ)VSμandλat1ststate图6 第一状态下p2(σ)随μ和λ的变化曲线Fig6 p2(σ)VSμandλat1ststate图7 第一状态下p1(σH)随μ和λ的变化曲线Fig7 p1(σH)VSμandλat1ststate图8 第一状态下p2(σH)随μ和λ的变化曲线Fig8 p2(σH)VSμandλat1ststate图9 第一状态下σ01(d)随μ和λ的变化曲线Fig9 σ01(d)VSμandλat1ststate图10 第一状态下σ02(d)随μ和λ的变化曲线Fig10 σ02(d)VSμandλat1ststate图11 第一状态下p1(ω)随μ和λ的变化曲线Fig11 p1(ω)VSμandλat1ststate图12 第一状态下p2(ω)随μ和λ的变化曲线Fig12 p2(ω)VSμandλat1ststate

图13 第二状态下p1(a)随μ和λ的变化曲线Fig13 p1(a)VSμandλat2ndstate图14 第二状态下p2(a)随μ和λ的变化曲线Fig14 p2(a)VSμandλat2ndstate图15 第二状态下p1(σ)随μ和λ的变化曲线Fig15 p1(σ)VSμandλat2ndstate图16 第二状态下p2(σ)随μ和λ的变化曲线Fig16 p2(σ)VSμandλat2ndstate图17 第二状态下p1(σH)随μ和λ的变化曲线Fig17 p1(σH)VSμandλat2ndstate图18 第二状态下p2(σH)随μ和λ的变化曲线Fig18 p2(σH)VSμandλat2ndstate图19 第二状态下σ01(d)随μ和λ的变化曲线Fig19 σ01(d)VSμandλat2ndstate图20 第二状态下σ02(d)随μ和λ的变化曲线Fig20 σ02(d)VSμandλat2ndstate

由图5、图6与图15、图16可以看出,不论一二级减振系统的频率比λ、质量比μ怎么配置,一级被减振部件上的加速度响应均方根值总是被降低,二级被减振部件上的加速度响应均方根值在λ<0.4之前总是被降低;一级被减振部件上的加速度响应均方根值在λ<1时随λ的增大而降低,在λ≤1之前达到极小值,之后随λ的增大而增大,并且这种变化规律还受到μ的影响,μ越大受λ影响的区间越大、降低的幅度越大;二级被减振部件上的加速度响应均方根值在λ<1时随λ的增大而增大,在λ≈1时达到极大值,之后随λ的增大而降低,并且这种变化规律还受到μ的影响,μ越小增大的幅度越大,甚至远远超过单层减振时的情形;在μ<1并且λ<0.1时,一级被减振部件上的加速度响应均方根值基本不受二级减振的影响;二级被减振部件上的加速度响应均方根值在λ<0.2时基本不受一级减振的影响,在λ>4时表现为一级减振系统的加速度响应均方根值,随μ的增大而减小,此时二级减振系统相对一级减振系统可以看作是刚体。

由图7与图17可以看出,对于两类双层减振形式,一级被减振部件上的高频响应除在λ=1附近区间发生突变外(这主要是由于阻尼比不同造成的,下面会讨论),随λ与μ的变化规律基本一致,即:在λ<0.1时基本不受二级减振的影响;μ越大影响越大,当μ≤0.2时,一级被减振部件上的高频响应除在λ=1附近区间发生波动外,在λ的其他区间几乎不发生变化。由图8与图18可以看出,对于两类双层减振形式,二级被减振部件上的高频响应除在λ=1附近区间发生突变外(这主要是由于阻尼比不同造成的,下面会讨论),随λ与μ的变化规律基本一致,即:λ越小或μ越大高频衰减性能越好;在λ<0.2时基本不受一级减振的影响;在很宽的λ区间内都具有优良的高频衰减性能。

由图9、图10与图19、图20可以看出,一级被减振部件相对基础的位移均方根值随μ的增大而增大,在μ<0.2时随λ的变化规律与加速度均方根值随λ的变化规律相似,在μ>0.8时随λ的增大而增大,在λ>1以后变得平缓;二级被减振部件相对一级被减振部件的位移均方根值除在λ≈1的临近区间出现一个小的波动外均随λ的增大而迅速减小,在λ<0.6时几乎不受μ的影响,在λ>0.6时随μ的增大而减小。

由图11、图12可以看出,不论一二级减振系统的频率比λ、质量比μ怎么配置,双层减振系统的低阶频率总是被向下偏离、高阶频率总是被向上偏离;低阶频率向下偏离的程度随λ的增大而减小,在λ=1时达到极小值,之后随λ的增大有所提高,但幅度很小;高阶频率向上偏离的程度随λ的增大而增大,在λ=1时达到极大值,之后随λ的增大有所减小,但幅度很小;低阶频率和高阶频率的偏离幅度均随μ的增大而增大。

2.4 阻尼比对响应特性的影响规律

图21～图28所示分别为在阻尼配置的第三种状态下(ζ01=0.125、ζ02=0.05),双层减振系统的各响应特性参数p1(a)、p2(a)、p1(σ)、p2(σ)、p1(σH)、p2(σH)、σ01(d)、σ02(d)随μ和λ的变化曲线。图29～图36所示分别为在阻尼配置的第四种状态下(ζ01=0.125、ζ02=0.25),双层减振系统的各响应特性参数p1(a)、p2(a)、p1(σ)、p2(σ)、p1(σH)、p2(σH)、σ01(d)、σ02(d)随μ和λ的变化曲线。

比较图3与图21可以看出,阻尼比γ的减小会使一级被减振部件上加速度响应峰值随λ的变化规律在λ≤1附近区间产生逆变,从而使得加速度响应峰值在λ≤1的一个区间内随λ的增加而升高,在λ≈1附近取得极大值,并且μ越大该极大值越大、受影响的λ区间越大,该极大值甚至远远超过单层减振时的峰值,从而破坏了前面得出的一级被减振部件上加速度响应峰值总是被降低的规律;除了在λ≈1附近区间产生逆变外,前面得出的其他结论基本不变。比较图3与图29可以看出,γ的增加不会改变一级被减振部件上加速度响应峰值随λ和μ的变化规律,只是使其在λ≈1附近取得的极小值进一步降低。比较图3、图13、图21、图29还可以得出一个结论,即:在γ≥1时,一级被减振部件上加速度响应峰值随λ和μ的变化规律以及总是被降低的态势保持不变;在γ<1时,一级被减振部件上加速度响应峰值随λ的变化曲线在λ≈1附近区域将会产生逆变。

图21 第三状态下p1(a)随μ和λ的变化曲线Fig21 p1(a)VSμandλat3rdstate图22 第三状态下p2(a)随μ和λ的变化曲线Fig22 p2(a)VSμandλat3rdstate图23 第三状态下p1(σ)随μ和λ的变化曲线Fig23 p1(σ)VSμandλat3rdstate图24 第三状态下p2(σ)随μ和λ的变化曲线Fig24 p2(σ)VSμandλat3rdstate图25 第三状态下p1(σH)随μ和λ的变化曲线Fig25 p1(σH)VSμandλat3rdstate图26 第三状态下p2(σH)随μ和λ的变化曲线Fig26 p2(σH)VSμandλat3rdstate图27 第三状态下σ01(d)随μ和λ的变化曲线Fig27 σ01(d)VSμandλat3rdstate图28 第三状态下σ02(d)随μ和λ的变化曲线Fig28 σ02(d)VSμandλat3rdstate

比较图4、图14、图22、图30可以看出,阻尼比γ基本不影响二级被减振部件上加速度响应峰值随λ和μ的变化规律;二级被减振部件上加速度响应峰值在λ≈1时的极大值不仅受到γ的影响(参见图38),更显著地受到一二级减振系统实际阻尼值ζ01、ζ02的影响,且ζ01或ζ02降低均会使该极大值急剧变大。

比较图5、图15、图23、图31可以看出,阻尼比γ对一级被减振部件上加速度响应均方根值随λ和μ变化规律的影响与对一级被减振部件上加速度响应峰值的影响基本一致,即:在阻尼比γ≥1时,一级被减振部件上加速度响应均方根值随λ和μ的变化规律以及总是被降低的态势保持不变;在γ<1时,一级被减振部件上加速度响应均方根值随λ的变化曲线在λ≈1附近区间就会产生逆变。

比较图6、图16、图24、图32可以看出,γ对二级被减振部件上加速度响应均方根值随λ和μ变化规律的影响与对二级被减振部件上加速度响应峰值的影响基本一致。

比较图7、图17、图25、图33可以看出,γ对一级被减振部件上高频响应随λ和μ变化规律的影响主要表现在λ≈1附近区间,即:γ≤1时,高频响应在λ≈1附近区间减小;γ>1时,高频响应在λ≈1附近区间增大;增大或减小的幅度不仅取决于γ(参见图41),更显著地取决于两级减振系统的实际阻尼值ζ01、ζ02;高频响应随ζ01或ζ02的增大而增大、高频衰减性能随ζ01或ζ02的增大而降低,高频响应随ζ01或ζ02的减小而减小、高频衰减性能随ζ01或ζ02的减小而提高;μ越小,所受的影响越大。

比较图8、图18、图26、图34可以看出,不论γ<1还是γ>1,都会使二级被减振部件上的高频响应在λ≈1附近区域显著增大,且μ越小,增大的幅度越大;γ<1时,二级被减振部件上的高频响应在λ<0.6的区间减小、在λ>1的区间增大;γ>1时,二级被减振部件上的高频响应在λ<1的区间增大、在λ>2的区间减小。

比较图9、图19、图27、图35可以看出,在μ<0.2时,γ对一级被减振部件相对基础的位移均方根值随λ和μ变化规律的影响与对一级被减振部件加速度均方根值的影响基本一致;μ>0.8时, 一级被减振部件相对基础的位移均方根值不仅受γ的影响(参见图43),更显著地受到两级减振系统的实际阻尼值ζ01、ζ02的影响,随ζ01或ζ02的增大而减小、随ζ01或ζ02的减小而增大。

比较图10、图20、图28、图36可以看出,γ对二级被减振部件相对一级被减振部件的位移均方根值随λ和μ变化规律的影响与对二级被减振部件上加速度响应均方根值的影响基本一致;二级被减振部件相对一级被减振部件的位移均方根值不仅受γ的影响(参见图44),更显著地受到两级减振系统的实际阻尼值ζ01、ζ02的影响,随ζ01或ζ02的增大而减小、随ζ01或ζ02的减小而增大。

从上面的分析可以知道,阻尼比γ对双层减振系统动力学特性的影响在λ≈1附近区间表现得最为显著。为进一步研究其影响,仍然分两种情形进行讨论,第一种情形是令λ=1、ζ01=0.125,分析ζ02的取值在0.01～1.0范围内(γ的取值范围为0.08～8.0)变动时对减振系统响应特性的影响规律;第二种情形是令λ=1、ζ01=0.05,分析ζ02的取值在0.01～1.0范围内(γ的取值范围为0.2～20)变动时对减振系统响应特性的影响规律。第一种情形的计算结果如图37～图44所示。第二种情形的计算结果除纵坐标数值有所差异外,曲线随γ(注意,不是随ζ02)的变化形状与图37～图44的形状基本一致,这里由于篇幅所限不再给出。这说明,这些动力学响应曲线的变化规律受γ的影响,具体幅值受ζ01与ζ02的影响。

由图37～图44可以看出,一级被减振部件的加速度响应峰值、加速度响应均方根值、相对位移均方根值均随γ的增大而减小,在γ达到某一阈值后减小幅度迅速变缓,μ越大阈值越小;二级被减振部件的加速度响应峰值、加速度响应均方根值、相对位移均方根值均先随γ的增大而减小,在某点处达到极小值,然后随γ的增大而缓慢增大,μ越大曲线变化越平缓;一级被减振部件的高频响应随γ的增大而增大(即高频衰减性能随γ的增大而降低);二级被减振部件的高频响应先随γ的增大而减小,在某点处达到极小值,然后随γ的增大而迅速增大。

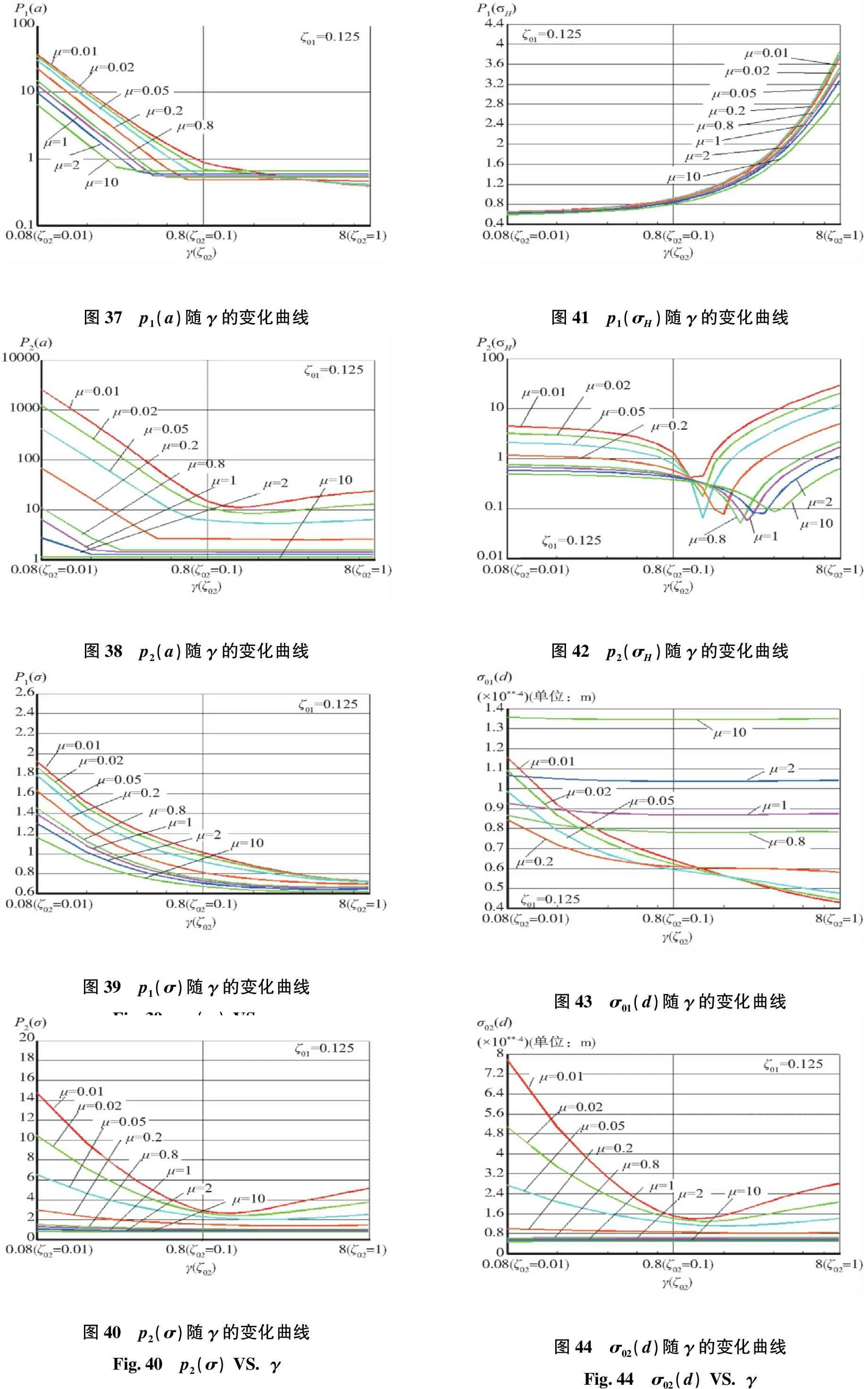
图37 p1(a)随γ的变化曲线Fig37 p1(a)VSγ图38 p2(a)随γ的变化曲线Fig38 p2(a)VSγ图39 p1(σ)随γ的变化曲线Fig39 p1(σ)VSγ图40 p2(σ)随γ的变化曲线Fig40 p2(σ)VSγ图41 p1(σH)随γ的变化曲线Fig41 p1(σH)VSγ图42 p2(σH)随γ的变化曲线Fig42 p2(σH)VSγ图43 σ01(d)随γ的变化曲线Fig43 σ01(d)VSγ图44 σ02(d)随γ的变化曲线Fig44 σ02(d)VSγ

3 总结与讨论

前面我们针对双层减振的两种形式详细研究了两级减振系统的频率比、质量比、阻尼比对双层减振系统在宽带随机振动激励条件下一级被减振部件和二级被减振部件的加速度响应峰值、全频段加速度响应均方根值、高频段加速度响应均方根值、相对位移均方根值、频率偏移等动力学响应参数的影响规律,得出了一般性的结论。可以看出,这三个设计参数对双层减振系统响应特性的影响规律还是比较复杂的,同一设计参数对不同响应特性参数的影响规律也是不一致的,甚至是相反的。在弹上电子设备的双层减振设计中,如果不能配置好这些设计参数,不仅不能实现进一步减振的目的,甚至还会适得其反,所以必须要依据我们已经得到的这些一般性规律并结合弹上电子设备的具体情况和减振设计的具体要求进行合理设计。下面简要讨论几种情况。

对于弹上电子设备,减振设计的中心目标一般可分为三种情况。第一种情况是,弹上电子设备结构刚度较好、高频响应较小,此时,只要减小减振系统全频段的加速度响应均方根值即可达到减振的目的。第二种情况是,弹上电子设备结构刚度不好、高频响应很大,远远超过减振系统的全频段加速度响应均方根值,此时,减振设计的中心目标是尽可能地降低减振系统的高频响应,以使载体上的振动环境条件经过减振系统后传递给弹上电子设备的高频激励足够小。第三种情况介于第一、第二种情况之间,既需要减小减振系统全频段的加速度响应均方根值，又需要降低减振系统的高频响应。对于第一种情况,可以考虑将二级减振系统设计成动力吸振器,将被减振部件放置在一级减振系统,根据质量比μ将频率比λ设计在0.5～1.0之间,并确保阻尼比γ≥1,然后根据相对位移约束、偏频约束以及二级被减振部件能够承受的最严酷力学环境要求等约束条件调整μ及阻尼值ζ01、ζ02。对于第二种情况,则需要充分利用双层减振设计中二级减振系统优良的高频衰减特性,在相对位移允许的情况下设计频率比λ越小越好,在0.6≤λ≤2时还要确保γ≈1,在此基础上根据其他约束条件调整μ及阻尼值ζ01或ζ02。对于第三种情况,则需要使λ≤0.6并确保γ≈1,在此基础上根据其他约束条件调整μ及阻尼值ζ01或ζ02。

对于减振系统安装在刚度较小的柔性支撑结构上这类特殊的双层减振情形,在被减振部件质量小于支撑结构第一阶模态质量的情况下,务必要使减振系统的频率远离减振系统安装于支撑结构上后支撑结构的第一阶振动频率,否则,减振系统的响应会被显著放大。即使在被减振部件质量大于支撑结构第一阶模态质量的情况下,也最好使减振系统的频率低于支撑结构的第一阶振动频率。同理,在弹上电子设备的地面振动试验中,务必使振动工装的刚度足够大,否则将会对试验结果的真实性带来不可忽视的影响。

[1] 屈维德.机械振动手册[M].北京: 机械工业出版社, 1992.

[2] 闻邦椿.机械振动学[M].北京:冶金工业出版社, 2011.

[3] 汪军.两类不同振动下的动力吸振器[J].辽宁工程技术大学学报(自然科学版), 1999，18(2):144-147.

[4] 常辉兰.随机激振下双层减振问题的分析[J]. 华侨大学学报(自然科学版), 1997，18(1):21-26.

[5] 谢燕, 雷勇军, 周建平，等.惯导减振系统结构参数的优化[J].强度与环境, 2005，32(4):39-45.

Study on the Laws of Effect of Structural Parameters on the Vibration-Absorption Characteristics of Missile-borne ElectronicEquipments Double-layer Vibration Isolating System

YAO Jian-jun, XIANG Wei-rong, YAN Hong-song, ZHEN Rui, YU Sheng-qiang

(Beijing Institute of Automatic Control Equipment, Beijing 100074, China)

Facing the matters about structural parameters design of missile-borne electronic equipments double-layer vibration isolating system, the laws that how the frequency ratio, mass ratio and damp ratio of the 2nd layer vibration isolating system to the 1st layer vibration isolating system affecting acceleration peak value response, root mean square value of acceleration response in the whole frequency range, root mean square value of acceleration response in a higher frequency range, root mean square value of relative displacement response, coupling frequency of electronic equipments under random vibration excitation are studied, and some universal conclusions are drawn. Then the way to apply the double-layer vibration isolating technologies is discussed. The conclusions can be used to direct the design of double-layer vibration isolating system for well vibration-absorption.

Double-layer vibration isolating; Random vibration; Response characteristics

10.19306/j.cnki.2095-8110.2017.01.018

2016-09-20；

2016-10-10。

姚建军(1974-)，男，博士，研究员，主要从事多物理场仿真分析与结构功能一体化设计方面的研究。

U666.12

A

2095-8110(2017)01-0098-12