冷却塔涡轮机全椭圆轴向出水蜗壳的水力设计

芦 月，屈 波，何中伟，栗文玲，刘佳佳

(1.河海大学能源与电气学院，南京 211100；2.河海大学水利水电学院，南京 210098)

0 引 言

在大型机械通风冷却塔中，由于风筒直径、高度等尺寸限制，传统冷却塔专用超低比转速混流式涡轮机的外形尺寸与结构布置受到了极大的限制[1,2]。前人对此类问题也做了部分研究。郑源教授在结构方面提出了金属梯形和单列环形导叶[3]；张丽敏[4,5]提出一种用于冷却塔的超低比转数混流式水轮机，并通过模型试验确定了新设计机组性能的稳定，满足冷却塔要求;齐学义[6,7]对冷却塔内水轮机蜗壳进行对比分析，对蜗壳中水流遵循速度矩为常数规律运动的非圆形断面水力设计进行分析；王旭[8]对水轮机椭圆蜗壳断面不同比例进行模型试验，得出较优模型断面；Lanjin Zhang[9]通过对冷却塔混流式水轮机蜗壳断面进行测量，发现纵横比为1.2时冷却效果最好；Klyukach A A等[10,11]人对已设计的椭圆蜗壳潮流能水轮机的空化性能进行数值模拟，验证其空化性能；前人虽对冷却塔中混流式水轮机蜗壳进行了一定研究，但对全椭圆轴向出水蜗壳研究较少，为实现现有冷却塔的节能改造，本文研发一种新型的、直驱于大型水冷塔风机并且适合冷却塔现有结构的超低比转速涡轮机理论设计方法，并通过数值模拟计算和水力性能分析，验证设计方法的准确性和可行性。

1 全椭圆断面轴向出水蜗壳的设计及内部水流的流动研究

蜗壳是涡轮机两个导流部件之一，其功能是将有压水流引导进入涡轮机转轮[12]，在外部条件允许的范围内，蜗壳的设计，应本着水流的能量损失尽可能小[13,14]，并且具有轴对称性的均匀出流[15]。采用椭圆形轴向出水蜗壳的设计，是为了在流速系数相同的条件下[16,17]，能够减小蜗壳控制机组径向尺寸[18]，更适合空间有限的冷却塔使用[19,20]。

1.1 涡轮机蜗壳的设计

与传统涡轮机中蜗壳、座环和转轮在同一平面安装，蜗壳垂直主轴水平出水的方式不同，本文所设计的特型涡轮机其蜗壳、座环、涡轮室为不同平面上下叠加安装的结构，即蜗壳下端和座环上端连接，座环下端和涡轮室上端连接，水流从蜗壳下端的圆环形出口轴向流入座环，然后从座环的下端轴向流入涡轮室，如涡轮机结构图(图1)所示。

1-涡轮机主轴；2-蜗壳；3-座环；4-涡轮室；5-涡轮机涡轮；6-尾水管图1 涡轮机结构图Fig.1 Structure diagram of turbine

为减少导水机构中的能量损失及得到工作转轮区域的均匀水流，从冷却塔循环水管引水至导水机构应首先满足轴对称性，因此蜗壳应满足以下要求：①应保证进入转轮的导水机构圆周流量均匀分布；②引水至导水机构的叶片应尽可能在额定工况下切向入水；③蜗壳的尺寸和形状在满足机组效率的前提下尽可能小。

因此，在稳定状态下，设计的蜗壳应满足：

(1)

为了更好地缩小机组径向尺寸，设计的蜗壳采用下出水、变椭圆形截面的特型蜗壳，设定其短、长半轴之比为：

(2)

通过上式计算可以确定蜗壳各断面的形状和尺寸，为了保证水流在蜗壳内的平滑过渡，在确定每个椭圆截面中心的布置高度时，采用按椭圆中心点连线展开为抛物线的形式，做出椭圆蜗壳标称流道断面图(如图2)。在接近喉部的部分，由于断面积渐小，为尽可能维持在相同半径的过轴环面中的轴向分速度、圆周分速度矩相同，在加大了过流断面积的同时，也加大了蜗壳中心轴线与水平面的夹角。

图2 椭圆蜗壳标称流道断面图Fig.2 Cross section of nominal flow passage of elliptical volute

1.2 涡轮机蜗壳内水流的流动研究

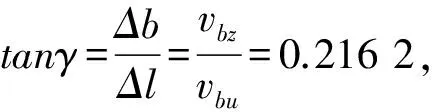
图3 蜗壳内单位流体速度三角形分解图Fig.3 Velocity triangle decomposition diagram of unit fluid in volute

涡轮机的导流部件包括蜗壳和导叶，是产生水流环量的关键部件，其水流特性近似为圆柱流，对于以涡轮机主轴为z轴的圆柱坐标系的导水机构内的流动微元，考虑到流体的均质、不可压缩、非黏性流体的假设，则有：

运动微分方程为：

(3)

连续性方程：

(4)

涡旋分量方程：

(5)

假设蜗壳内水流为不可压缩、非黏性的稳态轴对称有势流，则蜗壳内任意位置微元流体均满足：Ej=E，设作用于流体微元的力在各坐标的分量为：PQr、PQz，则式(3)、式(4)、式(5)得：

(6)

式中：PQ为由于流体微元圆周运动而附加的静压头。在稳态流动、不可压缩、非黏性的有势流体微元，其总能量保持不变，仅仅是动、静态压头内部的等值转换，结合式(6)根据总能量守恒，可以得出蜗壳内流速、压力分布：

(7)

式(7)即为蜗壳中速度与压力之间的能量关系式，由于本方程式不封闭，要根据具体的蜗壳形状及流动特点做一假设才能求解。

那么对于给定的导叶入口角度，就可以得出导叶入口的速度分布和静压分布。

对于导叶入口标称圆上，其径向速度为零；导叶入口外边圆上，其径向速度，方向指向涡轮机中轴；导叶入口内边圆上，其径向速度v0wr=-0.045 4 m/s，方向背离涡轮机中轴；所以导叶入口的设计为渐扩喇叭口。根据入口轴向流速可知：导叶入口宽度为：b0=0.144 1 m。

2 CFD三维数值模拟计算及验证分析

通过CFD对涡轮机进行全流道的三维建模、网格划分和数值模拟计算，模拟水轮机内部流场，较精确的预测水轮机的整体性能，并通过分析特型蜗壳的压力云图、速度云图和流线图等，验证特型蜗壳是否与理论设计相吻合，并进一步分析涡轮机的效率和蜗壳的水力损失，验证设计的特型蜗壳是否具有合理性和可行性。

2.1 模型建立

按照模型与原型比为1∶1的尺寸数据，利用大型三维建模软件UG对所设计的特型蜗壳进行三维造型，蜗壳鼻端直接与进口段相连，特型蜗壳三维图如图4所示。

图4 特型蜗壳三维建模图Fig.4 Special volute 3D modeling diagram

网格质量的好坏直接影响计算的敛散性及结果的精度，考虑到水轮机的结构较复杂，采用非结构化网格划分，使用ANSYS ICEM CFD对计算域进行网格划分。

2.2 数模验证结果及分析

假设水体为不可压缩黏性流体湍流，并且没有热量交换，故控制方程可以采用雷诺时均N-S离散方程，湍流模型选用k-omega SST模型, 为了保证计算精度，离散控制方程对压力项采用二阶中心差分格式，对动量方程式、湍动能、湍耗散方程采用二阶迎风差分格式，应用有限体积法对控制方程进行离散，采用SIMPLIC算法实现压力和速度的耦合求解[11]，设定收敛精度为0.000 001。根据设计水头10.5 m，机组转速为107 r/min，设定进出口边界条件为压力进口和压力出口，进行数值模拟。计算结果分析如下：

由涡轮机的整体流线图(图5)，可分析出涡轮机的整体流态较稳定，蜗壳内水流沿圆周方向对称均匀分布，在蜗壳下端出口处，水流以一定的角度偏转流入导叶，偏转角度与固定导叶叶形的设计相吻合，最终鼻端处的水流与入口处的水流汇合；导叶、转轮部分的整体流线较平稳，尾水管进口速度分布符合设计原理，轴向出水较平滑，没有出现涡旋和回流现象。设计工况下蜗壳流速矢量图如图6所示，在进口转弯的内侧区域流速较大，是由于蜗壳的鼻端直接与进口段相连，鼻端水流与进口水流汇合使流量突然增大而引起的，而从蜗壳外侧到内侧，流速沿径向对称均匀增大，流态较好，无涡旋产生。

图5 涡轮机整体流线图Fig.5 The overall flow chart of turbine

图6 蜗壳流速矢量图Fig.6 Flow velocity vectorgraph of turbine

为了进一步探究内部流场的分布情况，分别在包角0°、90°、180°和270°处做蜗壳纵向剖面图，断面处压力分布云图和速度分布云图如图7、图8所示。图7反映出蜗壳内的压力在靠近外壁面处最大，沿径向均匀递减，在靠近内壁面处最小；蜗壳内水流运动遵循伯努利方程，图8中速度的分布与压力的分布成反比，水流自外壁面到内壁面速度沿径向递增，符合半径大的地方速度小，半径小的地方速度大的规律。此外，压力和速度分布在圆周方向均具有较好的对称性，流场分布符合理论设计的规律。

图7 压力分布云图Fig.7 Pressure nephogram

图8 速度分布云图Fig.8 Velocity nephogram

图9为蜗壳出口速度矩矢量图，从图9中可以看出蜗壳出口为圆环形，出口处速度为对称均匀分布，内侧和外侧的速度方向均指向圆环标称圆处。在设计工况下，蜗壳出口的平均轴向流速为1.759 8 m/s。为验证新型下出水蜗壳符合理论设计中进入导叶珊的入口轴向分速度为常数的原则，在蜗壳出口截面上每隔15°包角取一条径向分割线，并通过CFD-Post后处理软件读出每条分割线上的平均轴向分速度值，轴向速度值随包角变化规律如图10所示。为验证蜗壳内不同包角的标称圆周方向水流速度为常数的设计理论，先读出平均标称圆圆周速度值为2.777 1，再每间隔15°包角读取速度值，标称圆圆周速度随包角变化规律如图10所示。

图9 蜗壳出口速度矢量图Fig.9 Velocity vectorgraph of volute exit

图10 蜗壳出口轴向速度及圆周速度分布规律 Fig.10 Distribution of axial velocity and peripheral speed of volute exit

从图10中可以看出轴向速度值的大小分布在1.7～1.8之间，不同包角处的轴向速度值近似相等；在0～20°包角处的轴向速度明显偏离设计工况下的理论值，这是因为在蜗壳进口处，流量较大、流态不稳定而造成轴向速度值升高；在340～360°包角处，速度值也有一定偏差，这是由于在蜗壳出口出，鼻端水流与进水管段水流汇流而使流量忽然增大，造成速度值升高。因此，可以认为蜗壳内进入导叶栅的入口轴向分速度为常数，与理论设计相符。对于标称圆圆周速度值的大小分布在2.7～2.9之间，与平均值近似相等，可以认为蜗壳内不同包角的标称圆周方向水流速度为常数，与理论设计相符。

为验证蜗壳内进入导叶珊的入口圆周分速度矩为常数的设计理论，先计算蜗壳出口处平均圆周速度矩的值为2.511 9，并在出口处的0°、180°和270°包角处随机选取若干点读取半径和圆周分速度值，再计算出随机点的圆周速度矩，由图11可以分析出随机点的圆周速度矩与计算所得的平均圆周速度矩的值基本相同，符合特型蜗壳的理论设计。

图11 蜗壳出口随机点圆周速度矩分布规律Fig.11 Distribution of random point peripheral speed moment of volute exit

表1反映了冷却塔专用涡轮机在设计工况下数值模拟的各工作参数，从表中可以分析出，涡轮机的出力高于风机的额定功率110，则能够平稳顺利地驱动风机旋转，保持冷却塔的正常工作状态；涡轮机的整体88.25%的效率很可观，说明所设计的涡轮机整体性能良好；通过计算各个过流部件的水头损失，可以分析过流部件的水力性能，由表1可知在转轮处的水头损失较大，说明大部分水流的能量在转轮处被转化为机械能，因此涡轮机的整体效率较高；所设计的特型下出水蜗壳的水头损失只有1.05%，说明特型蜗壳的水力性能较好。

表1 冷却塔专用涡轮机数值模拟各工作参数Tab.1 The working parameter of numerical simulation of turbine in cooling tower

3 结 语

(1)与传统水轮机不同，本文所设计的特型蜗壳采用全椭圆截面轴向出水的方式，将导水机构与蜗壳设置在不同平面，蜗壳、座环、涡轮为上下叠加的安装方式。

(2)通过全流道数值模拟分析表明，蜗壳出口处圆周分速度矩和轴向分速度均为常数，符合传统的设计理论。采用此特型蜗壳的冷却塔涡轮机效率可达到88.25%，蜗壳的水头损失为1.05%，具有较好的水力性能和运行稳定性。

(3)本文所设计的直驱于大型水冷塔风机的涡轮机其最大特点是显著减小了涡轮机的径向尺寸，便于安装和检修，并且能够实现传统电动风机冷却塔的节能改造，具有良好的经济效益和广泛的应用前景。

□

[1] 章志平, 屈 波, 栗文玲,等. 冷却塔水轮机椭圆蜗壳的设计与数值模拟[J]. 水电能源科学, 2016,(11).

[2] 张兰金, 阳 莉, 陈德新,等. 水力冷却塔水轮机的节能分析[J]. 可再生能源, 2012,(7):123-125.

[3] 郑 源, 张丽敏, 尹义武,等. 冷却塔中新型混流式水轮机设计[J]. 排灌机械工程学报, 2010,28(6):484-487.

[4] 张丽敏, 郑 源, 张成华,等. 用于冷却塔的超低比转数混流式水轮机设计[J]. 农业机械学报, 2010,41(S1):39-42.

[5] 朱 飞, 郑 源, 范小娟,等. 冷却塔内小型混流式水轮机的设计及数值模拟[J]. 水电能源科学, 2013,(7):165-168.

[6] 齐学义, 赵 强, 马惠萍,等. 全蜗壳的非圆形断面水力设计及其CFD分析验证[J]. 兰州理工大学学报, 2009,35(2):41-45.

[7] 齐学义, 晁文雄, 郝连松. 水轮机全蜗壳圆形断面的水力优化设计方法[J]. 兰州理工大学学报, 2012,38(3):43-46.

[8] 王 旭, 周琰杰. CFD数值模拟水轮机蜗壳三维设计[J]. 机械设计与制造, 2013,(10):17-18.

[9] Zhang L, Ren Y, Li Y, et al. Hydraulic characteristic of cooling tower francis turbine with different spiral casing and stay ring[J]. Energy Procedia, 2012,16:651-655.

[10] 王 飞, 王庆方, 王勇军,等. 水轮机蜗壳的优化设计与CFD分析[J]. 水利水电科技进展, 2012,32(5):86-88.

[11] Klyukach A A. Effect of Asymmetry of Spiral casing on vibration of generating set[J]. Power Technology and Engineering, 2014,47(6):408-415.

[12] Zhang L J, Wang L, Ren Y. Characteristic analysis of francis-turbine in cooling tower[J]. Applied Mechanics & Materials, 2012,190-191:57-59.

[13] Zhang L. Study on Francis Turbine with super-low specific speed applied in cooling towers[J]. Transactions of the Chinese Society for Agricultural Machinery, 2010:755-759.

[14] Zhou D, Chen H, Yang C. A highly efficient Francis turbine designed for energy recovery in cooling towers[J]. Advances in Mechanical Engineering, 2015,7(3).

[15] Ayli U E, Kaplan A, Cetinturk H, et al. CFD Analysis of 3D Flow for 1.4 MW Francis Turbine and Model Turbine Manufacturing[C]∥ ASME 2015 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. 2015.

[16] 熊 妍, 屈 波, 霍志红,等. 冷却塔专用超低比转速水轮机的设计及数值模拟[J]. 南水北调与水利科技, 2014,(3):112-115.

[17] 刘 娟, 张 琦. 水轮机技术在工业循环水冷却塔中的应用[J]. 山东化工, 2016,45(13):135-136.

[18] 王 旭, 李 萍, 陈荣盛,等. 水轮机椭圆蜗壳设计的CFD计算及试验分析[J]. 人民黄河, 2016,38(1):109-111.

[19] 黄 敏, 屈 波, 皮雪松,等. 冷却塔专用新型双级贯流式水轮机的转轮直径优化[J]. 机械制造与自动化, 2013,42(2):152-153.

[20] 姜 锋, 张建蓉, 叶文波,等. 混凝土蜗壳水力设计方法比较[J]. 水电自动化与大坝监测, 2014,(6):49-52.