基于SWMM模型的不同气象条件下城市雨水径流污染特性分析
2017-03-21肖存艳熊子鹰
蔡 甜,詹 健,肖存艳,熊子鹰
(南昌大学建筑工程学院,南昌 330031)
快速的城镇化进程使得城市植被大量减少,不透水面积不断扩大。据研究,原植被覆盖地表被不透水区替代后,地表下渗率由之前的70%~90%骤降至10%左右[1],导致雨水径流量急剧加大。城市雨水径流非点源污染是指地表累积的污染物被降雨冲刷汇入水系,造成受纳水体污染。
据相关资料统计,降雨径流污染在美国湖泊污染、河流污染中占到的比例分别为21%、45%[2],我国的非点源污染的主要贡献污染物为氮和磷,各占到了水体污染的81%和91%[3]。因此,雨水径流非点源污染引起了国内学者的高度重视,已有较多学者通过实测对各地区的非点源污染做了分析,如欧阳威[4]、李倩倩[5]等研究了不同下垫面类型下的非点源污染特性,并对污染物浓度之间的相关性进行了分析。马晓宇[6]等研究了不同重现期下城市非点源污染负荷,得出降雨强度与污染物浓度的关系。李家科[7]模拟了雨水花园对污染物浓度的削减率,评价了LID措施对污染物的控制效益。相对而言,基于SWMM水质模型来分析雨水径流非点源污染的研究并不多见,且鲜有学者系统地分析气象条件对径流污染的影响。据此,本文将气象条件这一概念引入模型,用于分析雨水径流非点源污染的特性,为非点源污染的监测和控制提供理论参考。
1 研究区概况及概化
本文选取南昌大学前湖校区东北侧区域作为研究区,该区域以密集型学生公寓、食堂、商业街为主,基本符合现代化城市特征。本研究区总占地面积为10.5 hm2,其中道路与屋面面积为6.72 hm2,绿地面积为3.75 hm2,绿化率为36%。研究区采用完全分流制雨水系统,雨水排放口设在研究区西南侧,雨水经排放口排放至校区内的润溪湖。根据研究区域的地形图,综合考虑土地利用类型并结合GIS软件将其划分为26个子汇水区,将雨水管网布概化为26个铰点和24条管段,管径为300~800 mm。导入SWMM模型的研究区概化图见图1。

图1 研究区概化图Fig.1 Generalization chart of the study area
2 模型建立与验证
2.1 模型建立
2.1.1 水文水动力模型
水文模型参数部分参照SWMM模型用户手册选取[8]。输入的水力参数主要包含入渗模型、曼宁系数以及洼地蓄水量。本文采用Horton入渗模型模拟雨水下渗,根据课题组之前对本地区的参数率定结果以及相关文献研究[9],本地区的最大入渗率fmax,最小入渗率fmin、衰减系数α分别为76、3.2 mm/h和3 1/h。不渗透地表和渗透性地表洼地蓄水量分别为5.04、1.51 mm。管道、不透水地表、透水地表的曼宁系数分别为0.011、0.013、0.4。地表汇流采用非线性水库模型,水动力模型采用动态波进行水质水量演算。
2.1.2 水质模型
水质模型采用完全混合一阶衰减模型,该模型认为径流在管道中混合快,浓度均匀且污染物不发生衰减,其理论方程如下:
(1)
式中:V为管道中水的体积,m3;Ci、C分别为管道进流、出流污染物浓度,kg/m3;Qi、Q分别为管道的入流量、出流量,m3/s;K为一级衰减系数;L为污染物的源汇项,kg/s。虽然该模型忽略了污染物在管道中的沉积,这可能对模型的精度产生一定的影响。但径流在管道中呈现冲刷强、历时短的现象,可近似认为污染物在管道中不发生衰减。
水质参数选用TSS、CODcr、TN、TP这4个具有代表性的雨水径流污染物作为模拟对象,根据研究区实际情况,设置屋面、道路、绿地3种不同土地利用类型。污染物的累积和冲刷分别采用饱和函数模型、指数冲刷模型。饱和函数模型需设定的参数分别为污染物最大累积量、半饱和天数;指数冲刷模型需设定的参数分别为冲刷系数、冲刷指数。设定道路清扫1 d 1次,参照郭琳等[10]对地表累积污染物的研究,清扫去除率设定为70%。
2.1.3 模型数据来源
模型输入数据的来源决定了模型的精度,前期的数据准备越精细、越切合实际,得到的模拟结果才会越真实。表1给出了本次建模的数据来源。

表1 模型的数据来源Tab.1 Data source of the model
2.2 模型验证
2.2.1 模型率定与误差分析
选用2016年9月15日、9月28日、10月21日的三场实测降雨对水质模型进行率定,以9月15日的降雨为例,该场降雨累计降雨量为12.19 mm,降雨历时2 h,污染物浓度的实测数据与模型拟合结果见图2。
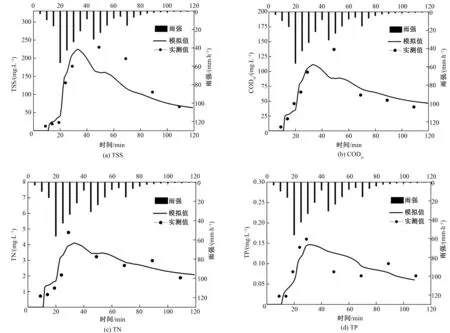
图2 实测数据与模型拟合图Fig.2 Measured data and model fit graph
通过以上数据可以看出:模型模拟的结果与实测数据吻合程度较高。具体模拟效果采用N-S(纳什系数)和平均相对误差RE来评价,平均相对误差小于±10%,N-S系数大于0.7,则表示模拟值与实测值较吻合[11]。N-S系数的定义如下:
(2)
式中:RNS为纳什系数;QS为污染物实测浓度,mg/L;Qm为污染物模拟浓度,mg/L;QP为污染物实测浓度平均值,mg/L。
平均相对误差RE计算公式如下:
(3)
式中:RE为平均相对误差,%;QS、Qm同公式(2);m为采样次数。经试验与计算得到污染物的RNS与RE见表2。

表2 污染物RNS与RE计算结果Tab.2 Pollutant RNS and RE calculation results
2.2.2 水质参数率定结果
TSS、CODcr、TN、TP的纳什系数分别均达到0.7以上,平均相对误差均小于±10%。说明模型建立得比较合理,能应用于该研究区的水质模拟。经率定确定的污染物累积和冲刷模型最终参数见表3。
3 模型应用
3.1 设计降雨数据的准备
本次模拟选用Keifer&Chu提出的芝加哥合成暴雨过程线法[12]模拟降水数据,通过查阅资料,南昌市的暴雨强度公式为:
(4)
式中:q为降雨强度,L/(s·hm2);P为重现期,a;t为降雨时刻,min。
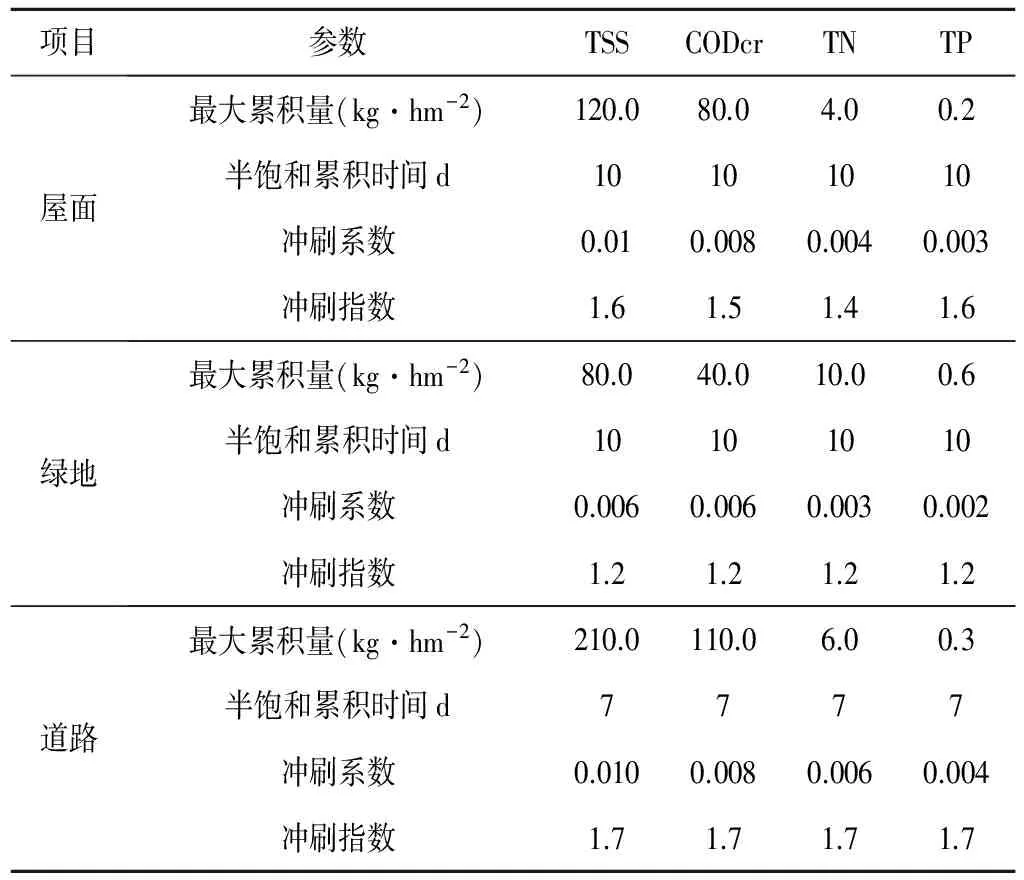
表3 污染物累积和冲刷模型参数值Tab.3 Contaminant accumulation and erosion model parameter values
将芝加哥雨型生成的不同重现期、不同雨峰系数下的降雨数据时间序列输入模型,降雨历时设定为2 h,得到不同的模拟结果。
3.2 不同重现期下污染物浓度的变化规律
南昌市的降雨大多以小重现期为主,在大重现期的情况下,人们更关心的是城市的内涝问题而非水质问题,因此小重现期对于水质模型有着更现实的意义。本次模拟选择0.05、0.1、0.2、1 a的重现期来分别模拟研究区的小雨(4.9 mm)、中雨(14.9 mm)、大雨(24.9 mm)以及暴雨(48.1 mm)情景;设定雨峰系数R=0.4,前期干旱天数为7 d。袁宏林等[13]对西安市降雨水质变化规律进行研究后,发现各类污染物主要黏附在固体颗粒上,说明CODcr、TN、TP与TSS有着良好的相关性;纪桂霞等[14]研究表明COD与TSS的相关系数甚至达到0.96。模拟结果显示:CODcr、TN、TP与TSS的浓度变化曲线呈现相同的变化规律。因此,本文以TSS为例研究不同重现期下污染物浓度随降雨历时的变化规律,模拟结果见图3。

图3 不同重现期下TSS浓度变化曲线Fig.3 TSS concentration curve under different reproducible periods
如图3所示,在相同的雨峰系数和干旱天数下,随着降雨强度的增大,不同重现期的污染物浓度峰值也逐渐由141 mg/L增大至598 mg/L。不难发现:浓度峰值的增幅随降雨强度的增大而逐渐变小,重现期从0.05 a提高到0.1 a,浓度峰值增加了189%;而重现期从0.2 a提高到1 a,浓度峰值仅增加8.5%,这可能是由于地表累积污染物的初始浓度有限,高强度降雨使得污染物的冲刷量接近累积量,所以冲刷量趋于饱和,浓度峰值增幅变小。图3中1年重现期的峰值形状变得尖而陡,这说明降雨强度越大,污染物的前期冲刷和后期衰减都越快。峰值出现时间在50~60 min,随着降雨强度的增大,峰值时间也会短幅度提前。从图3中还可以看出:在大雨和暴雨的情况下,污染物水质稳定后的浓度曲线甚至会低于较小强度降雨,这说明较高强度的降雨能够更快地将地表中的污染物冲刷干净。
3.3 不同雨峰系数下污染物浓度的变化规律
雨峰系数是降雨设计的重要参数,指在任意降雨历时下,自降雨开始至雨峰出现的时间与降雨历时的比值。雨峰系数越小,前期降雨强度越大,后期降雨强度则相对越小。据南昌市降雨统计资料显示,南昌市的短历时降雨(一般为2 h)的雨峰系数大多在0.3~0.4之间[15],但不排除雨峰靠前的情况。通过芝加哥雨型生成的降雨数据显示:在相同重现期下,改变雨峰系数对总降雨量几乎没有产生影响。据此,本文设计了P=0.1 a,降雨量为14.9 mm的一场中雨模拟污染物随降雨历时的污染特性;雨峰系数R分别设定为0.1、0.2、0.3、0.4;前期干旱天数设定为7 d。依然选用TSS浓度变化曲线为例,模拟结果如图4所示。

图4 不同雨峰系数下TSS浓度变化曲线Fig.4 TSS concentration curve under different rain peak coefficients
图4表明:在同一重现期和前期干旱天数下,不同的雨峰系数对TSS的浓度曲线会产生一定的影响。不难发现:雨峰系数每增大0.1,浓度峰值出现的时间推迟约10 min。此外,TSS的浓度峰值CR=0.4>CR=0.3>CR=0.2>CR=0.1,表明随着雨峰系数的增大,污染物的峰值浓度也会变大;这主要是由于雨峰系数对降雨强度产生影响:雨峰系数R值越大,降雨强度峰值越大,这与李文涛等[16]的模拟试验结果基本一致。所以随着雨峰系数的增大,更多的污染物被冲刷到径流雨水中,导致污染物的浓度峰值变大。雨峰系数R值越小,浓度峰值前的曲线越陡;这表明雨峰系数越小,降雨对前期地表累积污染物的冲刷作用越强。此外,4条曲线达到峰值后都逐渐递减,最终趋于同一稳定浓度。得出结论:雨峰系数只会影响污染物浓度的峰值与峰值时间,对最终稳定污染物浓度几乎没有影响。
3.4 不同干旱天数下污染物浓度的变化规律
雨水径流中的污染物浓度不仅受降雨冲刷影响,还与降雨前的地表污染物的累积浓度密切相关。本文引入前期干旱天数这一变量,是基于地表污染物累积的饱和函数提出的。饱和函数的公式如下:
(5)
式中:B为污染物累积量,kg/hm2;C1为污染物最大增长可能,kg/hm2;C2为半饱和常数;t为污染物累积时间,d。
饱和函数认为污染物的累积是一个与时间t的增函数且存在最大增长可能C1。模型设定重现期P=0.1 a,R=0.4;干旱天数依次设定为1、3、7、15 d。选取TSS浓度变化曲线为例,模拟结果如图5所示。

图5 不同干旱天数下的TSS浓度变化曲线Fig.5 TSS concentration curve under different drought days
图5表明:在同一重现期和雨峰系数下,前期干旱天数几乎不会影响污染物浓度峰值出现时间;峰值随干旱天数增多而增大且增长速率减缓,在间隔2、4、8 d的时间段内,峰值的平均增长率依次为65.7%、16.9%、4.8%,这一现象可通过以下数学公式求解:对饱和函数公式(4)两端分别求导,即得到污染物的累积速率B′,求导结果见下式:
(6)
式中:C1、C2与t的含义等同式(5),C1、C2均为常数且为正值,得出B′恒为正值且B′是关于时间t的减函数,说明地表污染物累积随干旱天数呈增长趋势,且增长速率越来越缓,最后达到饱和值。得出结论:前期干旱天数越多,雨水污染物的稳定浓度越高。
4 结论与建议
(1)通过对研究区域建立水质模型,分析了不同气象条件下的城市雨水径流污染特性。通过实测数据验证,认为模型具有较准确的模拟精度,能够用来辅助本区域的雨水管网设计和非点源污染控制。
(2)重现期、雨峰系数、前期干旱天数都会对径流污染物的浓度特性产生影响,其中重现期、雨峰系数影响污染物浓度峰值的大小和出现时间;干旱天数只影响污染物浓度峰值的大小以及浓度的变化趋势;降雨后期最终的稳定污染物浓度受重现期和前期干旱天数影响较大。
(3)在此水质模型的基础上,可根据气象部门提供的降雨强度、干旱天数等气象预报提前计算出各类污染物的平均EMC浓度,为初期雨水的收集与处理提供理论依据。
□
[1] Mitchell J G. Urban Sprawl, the American Dream[M]. National Geographic, July 2001:48-68.
[2] Chen J Y, Adams B J. Analytical urban storm water quality models based on pollutant buildup and washoff processed [J]. Journal of Environmental Engineering, 2006,132(10):1 314-1 330.
[3] Ongley E D,Xiaolan Z,Tao Y.Current status of agriculture and rural non-point source pollution assessment in China.[J].Environment Pollution,2010,158(5):1 159-1 168.
[4] 欧阳威,王 玮,郝芳华,等. 北京城区不同下垫面降雨径流产污特征分析[J]. 中国环境科学,2010,(9):1 249-1 256.
[5] 李倩倩,李铁龙,刘大喜,等. 天津市不同土地利用类型雨水径流污染特征[J]. 环境污染与防治,2011,(7):22-26.
[6] 马晓宇,朱元励,梅 琨,等. SWMM模型应用于城市住宅区非点源污染负荷模拟计算[J]. 环境科学研究,2012,(1):95-102.
[7] 李家科,李 亚,沈 冰,等. 基于SWMM模型的城市雨水花园调控措施的效果模拟[J]. 水力发电学报,2014,(4):60-67.
[8] Lewis A Rossman.Stormwater management model user's manual vision5.0[M].Cincinnati:USEPA,2010.
[9] 蒋元勇. 城市集水区降雨径流污染特征及调控模拟研究[D]. 南昌:南昌大学,2015:45-47.
[10] 郭 琳,曾光明,程运林. 城市街道地表物特性分析[J]. 中国环境监测,2003,(6):40-42.
[11] Bennis S,Crobeddu E.New runoff simulation model for small urban catchments[J].Journal of Hydrology Engineering,2007,12(5)540-544.
[12] Keifei C J,Hung C Y,Wolka K.Modified chicago hydrograph method.storm sewer design[M].Chicago:University of Illionois,1978.
[13] 袁宏林,陈海清,林 原,等. 西安市降雨水质变化规律分析[J]. 西安建筑科技大学学报(自然科学版),2011,(3):391-395.
[14] 纪桂霞,吴玲倩,金 敦,等. 城市小区雨水径流污染物监测及相关性研究[J]. 水资源与水工程学报,2010,(2):105-107,112.
[15] 吴雪军,杨就意. 南昌市青山湖排水区排涝规划技术介绍[J]. 中国给水排水,2015,(23):125-129.
[16] 李文涛,隋 军,刘成林,等. 设计降雨雨峰系数对排水管网设计流量的影响分析[J]. 净水技术,2015,(5):100-103,111.
