感潮河段双向波退水曲线耦合模型研究

张卫国，赵思远，顾巍巍，郝振纯

(1.宁波市水利水电规划设计研究院，浙江 宁波 315192；2.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098)

在目前洪水预报和模拟中，人们往往更重视洪峰流量的预报和模拟精度。但对于流域防洪调度而言，洪峰之后的退水过程直接关系到水库、闸泵等水利工程的调度运行方案和洪涝灾后评估，因此，对退水过程的精确模拟同样至关重要。20世纪60年代以来，随着水文模拟技术的发展与应用，水文学家对水文过程的形成及组成进行了较为系统的研究。退水过程作为水文过程的重要组成，人们逐步认识到退水过程的非线性[1-4]，基于水量平衡和流域产流机制，水文工作者提出了多种形式迥异的数学模拟模型，常用的退水模型包括Harris模型，Logistic模型、有理函数模型、指数模型和二次方模型等[3-7]。朱成涛等[5]提出采用一种关于时间t的线性函数或对数函数来对枯季径流退水曲线进行拟合预报；张端虎[6]以武江中上游赤溪水文站退水过程为例，对比了8种非线性退水曲线的模拟状况，发现时间二次方的反函数曲线模拟效果最好。翟然等[7]以清流河流域暴雨洪水为研究对象，系统分析了流域的退水过程特征，并验证了指数型退水模型能较好地模拟该流域退水过程。

尽管上述研究在各自研究区域都取得了较好的拟合效果，但是对于更为复杂的感潮河段退水阶段曲线拟合，由于洪水波与潮水波一体化的影响，上述方法不再具有适用性。而对于水动力计算模型，需要较详细的河道断面和糙率资料，实际应用难度较大。感潮河段的水流呈现复杂的周期性，具有不恒定往复流的特征[8,9]，对感潮河段进行退水曲线拟合研究，一方面对水文预报技术改进和水库运行调度等方面具有重要意义，另一方面可为水文规律的深化认识和水文模拟提供参考依据。本文将感潮河段退水曲线视作上游洪水波退水与下游潮水波顶托2种独立过程双向运动的叠加，以姚江出口姚江大闸站退水过程为研究对象，建立退水时序与潮汐调和的耦合模型，模拟场次洪水的退水过程。

1 感潮河段退水曲线耦合模型的建立

1.1 洪水波退水公式选定

洪水退水曲线是洪水消退过程线，是地表直接径流与浅层壤中流的综合反映。与单纯的地下径流退水过程不同的是，洪水退水过程由不同水源的径流成分组成，既包含地表径流的衰退，又包含地下径流的衰退。因其运动路径和受流域调蓄作用的不同，在特征上互有差异。此外，受河道断面形状、洪水波特性以及坡降等因素影响，不同流域的洪水退水曲线也是不同的。而由于退水曲线本身是一种寻求历史实际洪水系列变化规律来进行预报的方法[5]，对于一个特定的流域，其洪水波退水规律呈现出较好的重复性。

常用的退水模型包括Harris模型，Logistic模型、有理函数模型、指数模型和二次方模型等[3-7]。本文选用经前人验证模拟效果较好的有理函数[6]作为本次研究的洪水波退水曲线模型。其表达式如下：

(1)

式中：Zct为t时刻的洪水波拟合水位值；Z0为起始水位；a,b,c,d分别为待定系数，采用Levenberg-Marquardt迭代法求解(特点是速率快、精度高)。

1.2 潮水波预报模型选定

潮汐理论指出：由月球和太阳的引潮力引起的潮汐是多个余弦函数的叠加，每1个余弦函数可被定义成1个分潮。通过调和分析[10]建立潮水波预报模型为：

(2)

式中：Ht为t时刻的潮位预报值；A0为从某基准面算起的平均海平面高度；fq为分潮的交点因子；σq为分潮角速度；(v0+u)q为分潮的天文初相角；q为分潮的序号；Q为总分潮数；Hq为分潮的振幅；gq为分潮的专用迟角；Hq和gq合称为分潮调和常数。

本文选取甬江入海口镇海站包含丰、平、枯水年在内的2008-2012年的潮位资料为潮汐调和分析年组。根据5 a潮位资料采用自动分潮优选模式，基于最小二乘法原理求得各分潮的调和常数，再据此推求任意时刻的潮位。

1.3 双向波退水曲线耦合模型

假设感潮河段的洪水波和潮水波互不干扰，相互独立[8,9]，将感潮河段的洪水位视为洪水波和潮水波双向运动后的叠加，建立双向波退水曲线耦合模型。模型的基本方程以水位Zt为计算对象，分别由洪水波退水模型与潮水波预报模型叠加得到：

Zt=Zct+kPM24 hHt-τ

(3)

式中：Zct为洪水波拟合水位；Ht为预报潮位；τ为潮水波汇流时间，本文中为2 h。

姚江流域暴雨的出现常与台风天气有关，而台风对镇海站潮位有明显的增水作用，因此，为了接近实际的风暴潮位，本文考虑对调和分析预报的天文潮位增加2个控制变量，一个是潮水波影响系数k，单位为m-1；另一个变量是对应次洪在退水时刻之前已发生的最大24 h面降雨量PM24 h，单位为m。

1.4 目标函数

在进行退水过程模拟和参数率定时，首先根据场次洪水过程和降水终止时间，初步判断退水阶段，利用退水阶段的实测资料率定退水模型参数，选择Nash Sutcliffe效率系数NSC和均方根误差RMSE为目标函数进行参数率定和模型模拟效果评价：

(5)

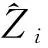
2 应用实例

2.1 基本资料

姚江为甬江的重要支流，位于我国海岸线中段，浙东沿海。其流域面积为1 879 km2(规划围垦后)，地势南高北低，流向自西向东。现状条件下，姚江流域东排出口仅姚江大闸1处排水口门，其出流能力受奉化江干流洪水以及甬江上溯潮水的双重制约影响。甬江流域水系及水情站点概化见图1。

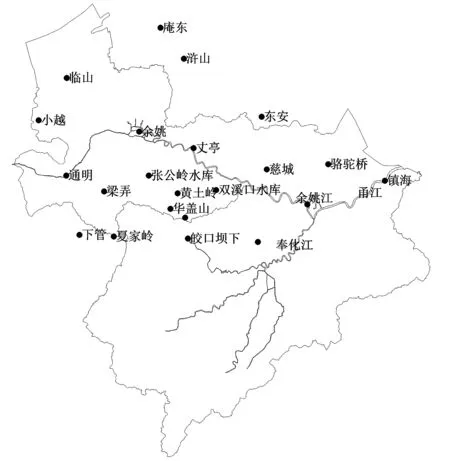
图1 甬江流域水系及水情站点概化

姚江大闸位于姚江入江口段，于1959年建成，出闸行3.3 km与奉化江汇合为甬江。本文选取姚江流域2008-2016年共15个场次洪水退水时段，收集整理了姚江大闸站典型暴雨时期逐时水位资料，以及流域内18个国家雨量站逐时暴雨摘录资料，通过泰森多边形法计算得到姚江流域典型暴雨时期面雨量特征值，见表1。

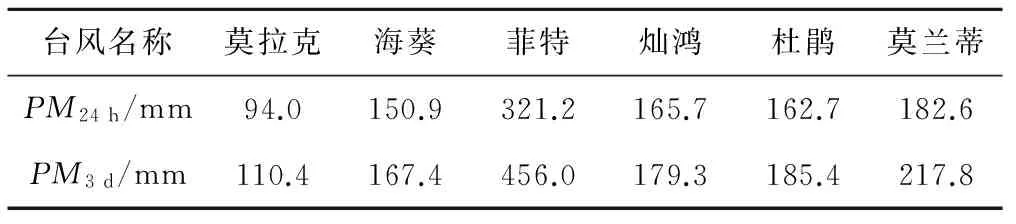
表1 姚江流域典型暴雨特征值

2.2 退水过程模拟

选定退水过程的起退水位作为起始零点，通过双向波退水曲线耦合模型模拟姚江流域东排出水口姚江大闸站的15场次洪水退水过程，表2统计给出了15场次洪的模型参数及模拟效果。为直观起见，图2给出了2场典型场次洪水的实测与模拟退水过程。

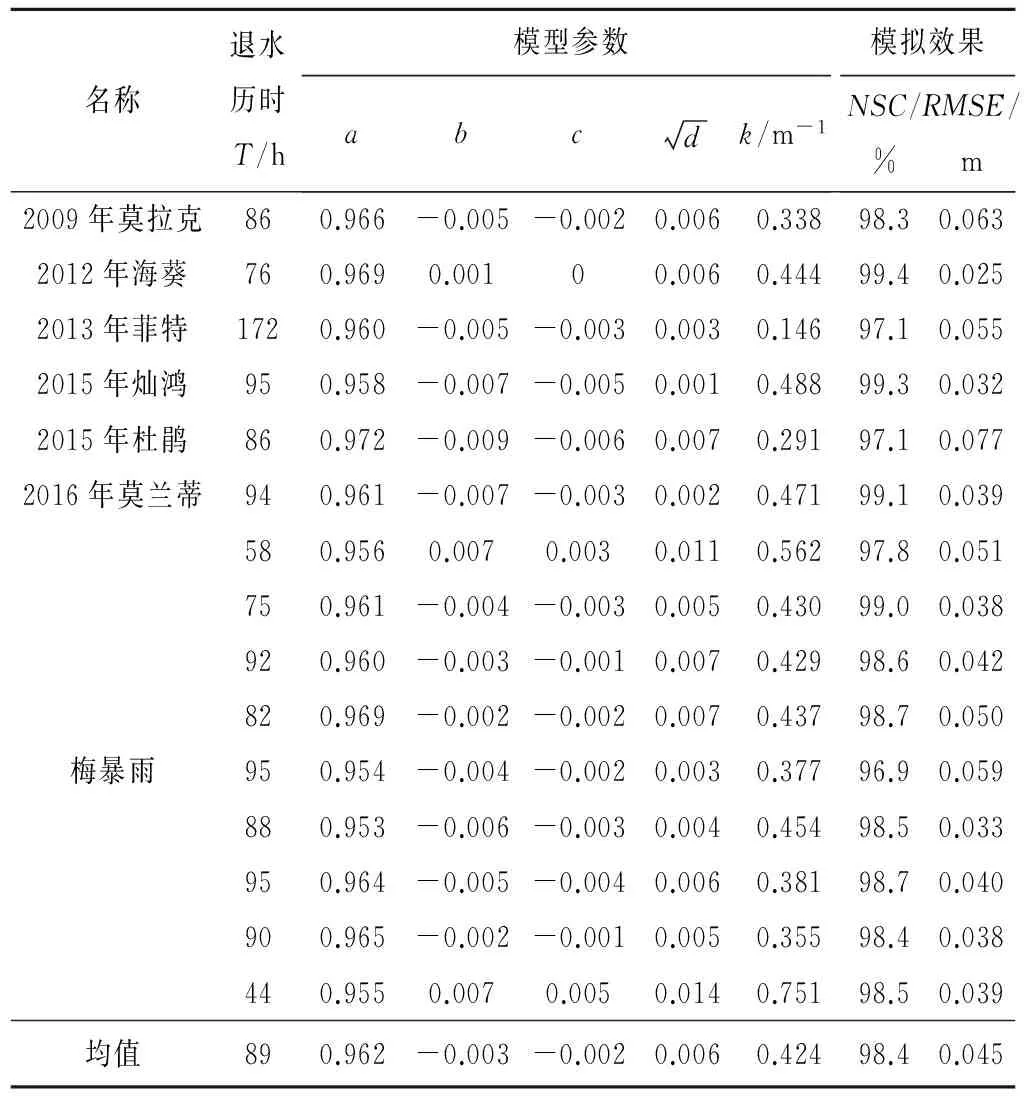
表2 典型暴雨期间退水模型参数及模拟效果

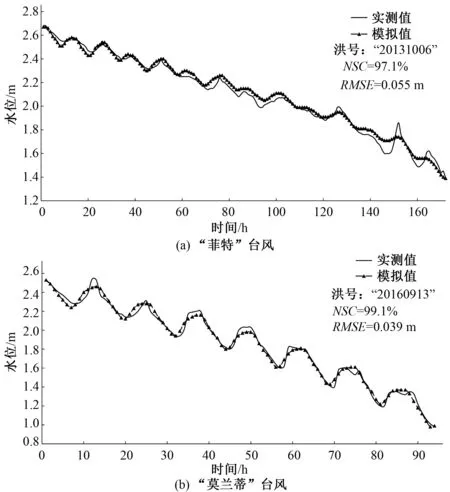
图2 典型场次洪水的实测与模拟退水过程比较

由表2可以看出：

(1)姚江流域场次洪水退水平均历时为89 h，其中，最大历时为172 h，为最小历时近4倍。次洪退水历时与降水历时有关，本次研究中持续时间最长的退水过程为“2013年菲特台风”期间所产生，经过统计，“菲特”期间姚江流域最大3 d降雨量达到100 a一遇标准，因而，持续且集中的降水导致本次地表径流历时也较长。

(2)洪水波退水模型的几个参数在各次洪退水过程中取值较为稳定，这也在一定程度上验证了前文表述的：对于一个特定的流域，其洪水波退水规律呈现出较好的重复性；与潮位有关的潮水波影响系数在不同次洪退水阶段略有差异，这是因为在次洪退水期间，还要考虑天文大潮出现的时间点。如“菲特”期间恰逢天文大潮，上游高洪水位与下游高潮位相互冲抵，且PM24 h较大，潮水波所占比重并不大，该系数为0.146 m-1。各次洪退水段潮水波影响系数平均为0.424 m-1，最大值为0.751 m-1。

(3)双向波退水曲线耦合模型能够较好地模拟姚江流域出口的退水过程，对各场次洪水的退水过程模拟的Nash Sutcliffe效果系数大多超过97%，其中最大Nash Sutcliffe效率系数为99.4%，最小的Nash Sutcliffe效率系数为96.9%，超过85%。从均方根误差来看，平均模拟误差为0.045 m，最大的模拟误差也仅为0.082 m。图2给出的典型次洪的实测与模拟退水过程比较可以看出，实测与模拟的退水曲线总体吻合良好，尽管对“菲特”台风造成的洪号为20131006的洪水退水过程的尾段模拟误差稍大，但并不影响总体的误差水平。另一场由“2016年莫兰蒂台风”所造成的20160913的洪退水阶段，虽然受潮位影响，河道水位起伏较大，但模型模拟效果良好，Nash Sutcliffe效率系数为99.1，均方根误差为0.039 m。

3 结 论

(1)次洪退水历时与降水历时有关，持续且集中的降水会导致本次地表径流历时也较长。各次洪退水段模型模拟的洪水波参数变化不大，较为稳定，说明对于一个特定的流域，其洪水波退水规律具有较好的重复性。潮水波影响系数的大小与河道水位、降水以及天文大潮的出现有关，尤其在梅雨季节，潮水波影响系数较为稳定，但当天文大潮出现时影响系数明显增大，各次洪退水段模型模拟的平均潮水波影响系数为0.424 m-1。

(2)双向波退水曲线耦合模型能够较好地模拟姚江流域出口的退水过程，对15场次洪水的退水过程模拟的Nash Sutcliffe效率系数超过96%，均方根误差平均为0.045 m。基于以上次洪退水过程模拟和参数分析，开展感潮河 段退水段实时预报是需要下一阶段进行研究验证的科学问题。

□

[1] Wittenberg H, Sivapalan M. Watershed groundwater balance estimation using streamflow recession analysis and baseflow separation[J]. Journal of Hydrology, 1999,219(1):20-33.

[2] Zecharias Y B, Brutsaert W. Recession characteristics of groundwater outflow from mountainous watersheds[J]. Water Resources Research, 1988,24(10):1 651-1 658.

[3] 李建柱,冯 平,王 勇.地下径流退水过程规律[J].天津大学学报(自然科学与工程技术版),2010,43(5):400-405.

[4] 苏 菊.基流分割的简便计算法[J].武汉大学学报(工学版),1986,19(4):10-17.

[5] 朱成涛,蹇德平,何朝晖,等.基于随时间变化退水系数的枯季径流预报方法研究[J].人民长江,2010,41(3):31-33.

[6] 张端虎.基于非线性回归的流域洪水退水曲线拟合方法研究[J].广东水利水电,2012,(7):25-27.

[7] 翟 然,王国庆,万思成,等.清流河流域场次洪水的退水特征及过程模拟[J].水资源与水工程学报,2015,26(3):1-4.

[8] 包为民,张小琴,瞿思敏,等.感潮河段双向波水位演算模型验证[J].水科学进展,2009,20(6):794-799.

[9] 王淑英,黄国如,周 维.考虑水位分级和退水段独立的感潮河段双向波水位演算[J].水利水运工程学报,2011,(2): 54-59.

[10] 徐汉兴.潮汐计算[M].北京:人民交通出版社,1998.