多源观测在水文数据同化中的应用
2017-03-21杨楚慧张秋汝史良胜
杨楚慧,林 琳,张秋汝,史良胜
(武汉大学水资源与水电工程国家重点实验室,武汉 430072)
流域水文模型被广泛应用于灌区管理和洪涝灾害防治等方面[1,2]。然而由于模型误差和观测误差等不确定性的影响,水文模型在进行径流等水文状态预报时存在不可避免的偏差[3]。因此,多目标函数自动调参、数据同化等方法[4,5]被用于修正误差来改善水文状态的估计。其中数据同化(data assimilation)由于综合考虑了各种误差来源,而被广泛应用于水文模型的参数校正和状态预测。水文数据同化通过向模型中连续加入观测数据来降低不确定性,最终提高模型预测能力。随着观测手段的迅速发展,数据同化技术在近年来得到了深入研究。
在水文数据同化模型中,研究者大多采用径流和土壤水等观测数据来进行流域水文状态的更新和参数估计。Xie和Zhang[6]利用径流观测准确地预测了径流及相关参数。Chen等[7]利用表层土壤含水量观测进行同化,发现深层土壤水和径流的估计值与实测有明显的偏差。Sun和Lee等[8,9]联合利用径流和土壤水观测进行同化,发现径流和土壤水状态的估计结果优于同化其中任一观测。此外,Shi等[10,11]用数值和实例验证了同时加入径流、地下水位、土壤水、以及蒸散发等多种观测对多参数估计的有效性,但不同的观测组合对于水文状态预测的影响仍有待讨论。其中地下水位作为一种简单经济的观测手段,受到上层土壤水补给和蒸发等因素的影响,能在一定程度上反映非饱和土壤水的变化情况,因此研究同化地下水位对于径流和土壤水的影响过程具有一定价值。
为了进一步研究多源观测对于水文数据同化的影响,本文使用集合卡尔曼滤波(EnKF)方法,与分布式水文模型SWAT结合,研究径流、土壤水和地下水位等观测在参数估计和状态预测方面的性能。
1 方法与试验
1.1 SWAT模型
SWAT(Soil and Water Assessment Tool)模型是由美国农业部农业研究中心(USDA)开发的半分布式水文模型。模型可以模拟多种水文循环物理过程,进行在长时间序列下不同土壤类型、土地利用和管理条件的复杂流域水文计算[12],在我国被广泛应用于水文模拟和非点源模拟等方面[13]。
在建立模型过程中,基于DEM数据,流域被划分成若干个子流域,并根据不同的下垫面条件进一步归类成若干个水文响应单元(HRU)[14]。SWAT模拟的逐日水文循环基于每个HRU的水量平衡方程进行,HRU是SWAT最基本的计算单元。
在进行降雨-径流计算时径流流量由3部分组成[12]:
Q=Qsurf+Qlat+Qgw
(1)
式中:Q为当日总径流量;Qsurf为地表径流量;Qlat为侧向径流量,(mmH2O);Qgw为当日流入河道的地下水径流量。
其中的地表径流量一般采用SCS曲线数法来计算,其计算方程如下:
(2)
式中:P为第i天的降水量;S为滞留参数,随土壤类型和土地利用等下垫面条件产生空间差异,随土壤含水量的变化产生时间差异,其定义公式为:
(3)
式中:CN为日曲线数,取决于CN2和前期土壤水分条件;CN2为土壤水分条件为一般湿润时的曲线数。
HRU计算单元的水量平衡总方程为:
(4)
式中:SWt为第i天的土壤含水量;SW0为土壤初始含水量;t为时间,d;Qsurf为地表径流量;ETi为第i天的实际蒸散发量;Wseep为从土壤剖面进入包气带的水量。
1.2 集合卡尔曼滤波
数据同化通过向系统中加入连续的观测来修正模型的变量状态[15],集合卡尔曼滤波(EnKF)是一种顺序数据同化算法,由于其较低的计算成本和简易灵活性,被广泛应用于水文领域。
水文模型在气象因子的驱动下状态和参数发生动态变化:
ut+1=f(ut,At+1)+wt+1
(5)
式中:u是水文状态值如径流、土壤水含量等;A是驱动因子如降水等;t是时间;w是误差项,代表模型误差、参数误差等的影响。
进行同化的状态向量由模型参数、状态变量和观测共同组成:
yt=[mTt,uTt,dTt]
(6)
式中:y是状态向量;m是估计的模型参数,本算例中为CN2;u是模型包含的状态变量,如径流量Q和土壤水含量SW等;d是观测值,包括径流、剖面土壤水含量和地下水位;t是时间序列。
其中观测值可表示为:
dt+1=G(mt,ut)+wt+1
(7)
式中:G(∶)表示模型状态和观测值之间的转换关系;w为观测误差。
对于t+1时刻的样本j,集合卡尔曼滤波的更新向量可表示为:
yat+1,j=ymt+1,j+Kj(dt+1,j-Hymt+1,j)
(8)
式中:y是状态向量;a和m分别代表最优估计值和预报值;d是观测值;H是观测矩阵,代表状态向量与观测向量之间的转换关系;K是卡尔曼增益,表示在同化过程中观测和状态值的权重:
Kt=CmHT[HCmHT+CD]-1
(9)
式中:Cm是状态向量的协方差矩阵;CD是观测误差矩阵;CmHT表示状态向量与观测向量的互协方差;HCmHT表示观测向量的自协方差,可以直接利用样本统计的方法得到。
2 算例研究
2.1 算例说明
为了验证径流、土壤水含量及地下水位等观测信息的作用,本文构造了一个虚拟的流域水文试验,使用漳河灌区的下垫面和气象资料,但调整了土壤类型及其分布。研究区总面积 1 089.7 km2,主要土地利用方式为落叶阔叶林(FRSD),主要土壤类型为黏土(56.57%)和黏壤土(43.43%)。建立模型的主要输入数据包括数字高程地形图(DEM)、土地利用及土壤类型图、日降水资料和其他气象数据。
在SWAT模型中输入以上数据后,根据DEM信息、土壤类型和土地利用方式,将流域划分成7个子流域(见图1),14个水文响应单元(HRU)。径流、土壤水含量及地下水位观测数据由已知参数的参照模型运行得到。
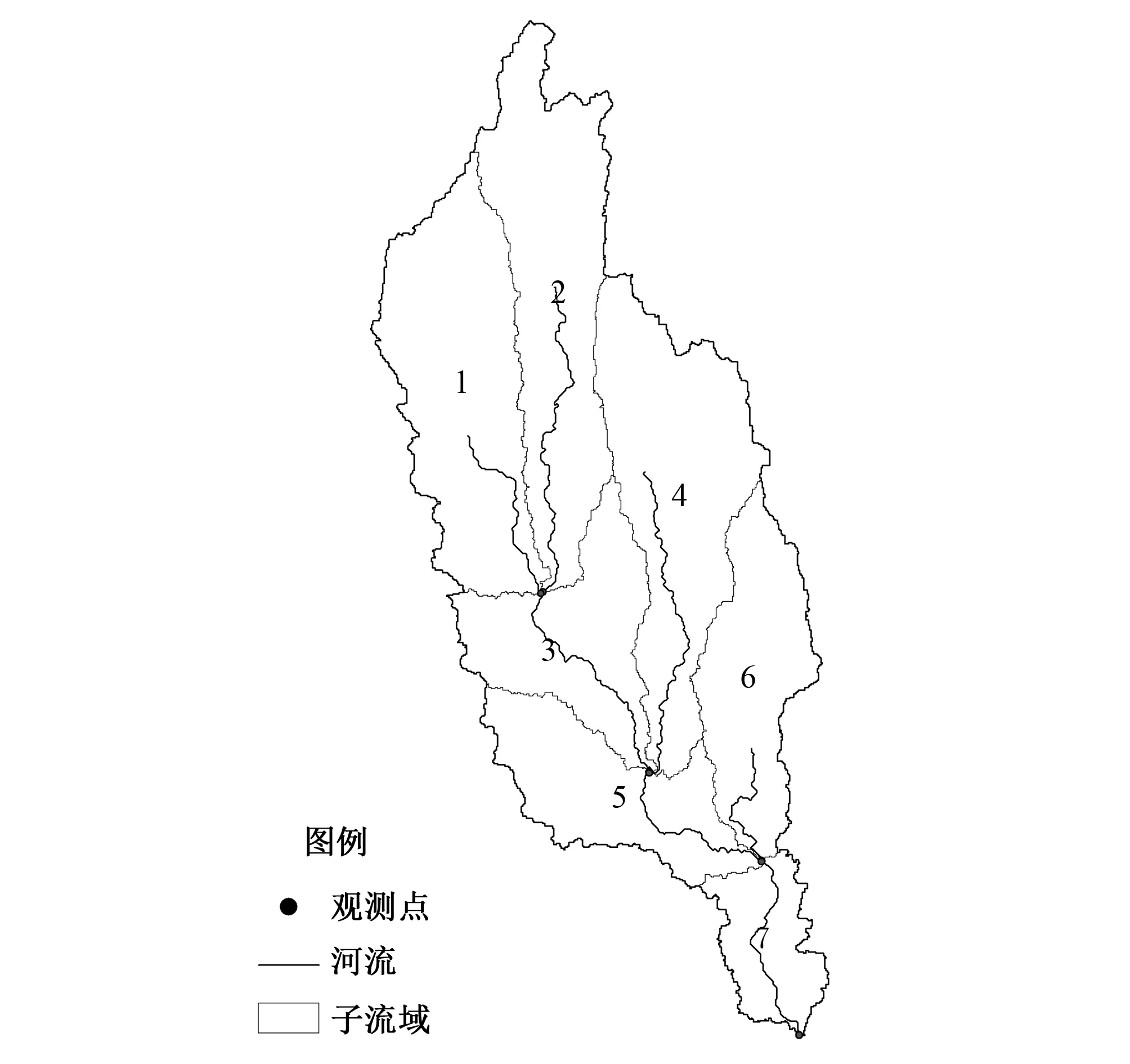
图1 研究区域DEM和子流域划分Fig.1 DEM and watershed delineation of research area
2.2 数据同化过程
整个模拟过程分为3个步骤:①预热期,在长期气象驱动下使模型达到合理的水文状态,运行时间为2001年1月1日至2004年1月1日;②扰动期,通过正态分布对参数进行扰动生成若干个样本,每一个样本独立向前演算,运行时间为2004年1月1日至2004年4月9日;③同化期,连续性地加入观测值来更新水文状态(径流和表层土壤含水量等)和模型参数CN2,从而得到更为准确的估计值,运行时间为2004年4月10日至2004年11月1日。
本文设置了4个算例。为了考虑影响径流估计的因素,设置算例1:仅加入流域出口处径流观测(见图1);算例2:仅加入流域表层5 cm土壤水观测;算例3:综合考虑以上2个算例,联合利用径流和表层含水量观测,来讨论多源观测对于提高模型状态描述的效果;算例4:同时加入径流和地下水位观测,来探讨地下水位对于反演土壤水状态的作用。
在上述算例中,所有算例估计的水文状态量都相同,包括径流Q和表层含水量SW等,不确定参数仅考虑CN2,其初始分布服从G(60,52),所有观测的频率为每日一次,径流观测相对误差为10%,土壤水观测相对误差为3%,地下水观测绝对误差为2 cm,土壤水和地下水模型误差为5%,计算样本共300个。
本文给出了参照解、EnKF解和非条件解来验证数据同化的效果。参照解是指在正确的参数和边界条件下的水文状态;EnKF解是在错误的初始参数条件下利用数据同化模型计算得到的结果;非条件解的初始参数和边界条件与EnKF解相同,但不进行参数更新和数据同化时得到的结果。
为了评价同化效果,使用均方根误差RMSE来量化模拟值与真实值之间的差异:
(10)
式中:n为计算单元数目,等于子流域或者HRU的个数;Y(xi)为参照值;Yt(xi)为同化后的样本均值。
3 分析及讨论
3.1 径流估计
图2描绘了加入不同观测时子流域7径流的时间变化,同时给出了参照解和非条件解。由图2可以看出,当加入的观测包含径流时,径流估计值与参照值十分接近;仅使用土壤水观测时,仅加入表层土壤水观测在雨季能较好地预测径流值,旱季时预测的径流与参照值有较大的偏差。

图2 子流域7加入不同观测时径流的时间变化 Fig.2 Estimated streamflow process in subbasin 7 when adding different observations
图3给出了整个流域径流RMSE的时间变化。图3中在加入径流观测后,无论是否加入其他类型观测,流域径流估计的RMSE都能迅速减小到接近0值;仅加入浅层土壤水时雨季的RMSE迅速降低,在旱季则会造成径流估计的恶化,RMSE值甚至大于非条件解。因此,仅需加入径流观测就能迅速校正径流预测值,而表层土壤含水量只能反映该子流域地表产流的过程,而无法反映基流过程,因此无法改善径流的估计效果。
由于流域出口处径流包含了所在子流域的产流信息和整个流域的汇流信息,可以利用该点的径流值反演上游各子流域的径流过程。因此,在估计流域径流时,对出口点的径流进行观测十分必要。算例1中虽然仅加入了流域出口处的径流观测,但数据同化后整个流域的径流预测都获得了改善,因此流域出口处径流对于整个流域的径流估计具有重要的价值,Xie[6]等人在研究中也提出了相似的观点。

图3 加入不同观测时流域径流的RMSEFig.3 RMSE series of streamflow when adding different observations
3.2 土壤水估计
图4为加入不同观测时子流域7中HRU 14的各层土壤含水量的RMSE变化情况。如图4(a)所示,利用径流观测可以较好地估计出表层土壤水,这是由于表层土壤含水量对径流产流过程有着强烈的影响,此时2者相关性较高。但随着土壤深度的增加,相关性的减弱,加入径流观测对深层土壤水估计效果的产生明显的偏差,且变化较为剧烈[见图4(b)和4(c)]。总体而言,加入径流观测对土壤剖面整体的含水量估计作用较弱。
仅利用表层土壤水观测时,深层土壤水估计会产生偏差,使得土壤水估计会发生剧烈变化[见图4(b)和4(c)],此时的RMSE也变化十分迅速。同时加入径流和表层土壤水观测能从一定程度上调整深层土壤水的偏离情况,图4中该算例的RMSE值在大部分情况下最小,说明同时加入这2种观测能调整模型偏差,使状态估计更加准确。
图4(c)中加入地下水和径流观测后的深层土壤水量RMSE也略小于仅加入径流观测,因此额外的地下水位数据能在一定程度上提高土壤含水量的估计效果。在SWAT中,补给和蒸发会影响地下水位的变化:在降雨较为强烈和持续的时候,土壤含水量的连续增加会导致地下水位的上升;土壤含水量的持续减小则会引起毛细作用的增强,并进一步带来地下水位的降低。因此,地下水位作为一种廉价的观测信息,可以用于改善土壤含水量估计。Shi等[11]研究发现,地下水位数据还可为土壤水参数的估计提供有用的信息。
3.3 CN2估计
图5分别使用估计值和参照值作为横纵坐标,反映所有HRU的CN2在同化期结束时的估计情况,若散点越接近45°线,则效果越好。从图5(b)、5(d)和5(e)中可以发现,加入径流的算例的CN2估计效果都比较均匀的分布在45°线左右,这是由于地表产流和CN2有强烈的相关性,因此仅加入流域出口点径流能较为准确的描述整个流域的径流过程,并获取合理的CN2参数。而本算例中没有考虑误差和观测点数目等因素的影响,可以在后续工作中进一步讨论。
而图5(c)使用仅表层5 cm土壤水观测来同化CN2值时,参数估计值普遍小于参照值,因此仅利用表层土壤水不能准确的估计流域参数。
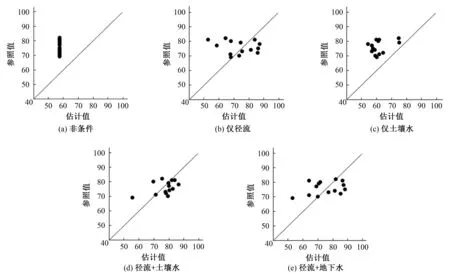
图5 CN2模拟值与参照值的比较Fig.5 Final results of CN2 final assimilation results compared to reference values
4 结 语
本文建立了基于分布式水文模型SWAT的数据同化方法,构造虚拟的流域水文模型,讨论了不同的观测数据对于水文变量预测和参数估计的价值。研究结果表明:①仅加入径流观测能获得较为准确的径流和CN2参数估计,但是深层土壤水估计会发生偏差;②加入表层含水量观测能模拟雨季的地表径流变化情况,但是利用表层土壤含水量估计深层的水分变化情况会产生较大的偏差,从而导致地下水补给和基流估计十分不准确,因此无法反映整个径流过程;③同时加入表层含水量和径流模型对状态的估计效果要略优于加入其中任何一种观测;④由于地下水位变化受到补给和蒸发的影响,地下水观测在一定程度上能反映土壤剖面含水量的变化趋势,从而提高土壤水的估计效果。
对于水文数据同化问题,若只需要了解径流过程,可以只加入径流观测进行同化,仅提供表层土壤水分信息无法获取根区含水量情况。成本低、易获取的地下水观测可以从一定程度上反映深层土壤水变化趋势。
□
[1] 芮孝芳, 蒋成煜, 张金存. 流域水文模型的发展[J]. 水文, 2006,26(3):22-26.
[2] 代俊峰, 崔远来. SWAT模型及其在灌区管理中的应用前景[J]. 中国农村水利水电, 2006,(6):34-36.
[3] 芮孝芳. 流域水文模型研究中的若干问题[J]. 水科学进展, 1997,8(1):94-98.
[4] Muleta M K, Nicklow J W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model[J]. Journal of Hydrology, 2005,306(1):127-145.
[5] Lei F, Huang C, Shen H, et al. Improving the estimation of hydrological states in the SWAT model via the ensemble Kalman smoother: synthetic experiments for the Heihe River Basin in northwest China[J]. Advances in Water Resources, 2014,67:32-45.
[6] Xie X, Zhang D. Data assimilation for distributed hydrological catchment modeling via ensemble Kalman filter[J]. Advances in Water Resources, 2010,33(6):678-690.
[7] Chen F, Crow W T, Starks P J, et al. Improving hydrologic predictions of a catchment model via assimilation of surface soil moisture[J]. Advances in Water Resources, 2011,34(4):526-536.
[8] Sun L, Seidou O, Nistor I, et al. Simultaneous assimilation of in situ soil moisture and streamflow in the SWAT model using the extended Kalman filter[J]. Journal of Hydrology, 2016,543:671-685.
[9] Lee H, Seo D J, Koren V. Assimilation of streamflow and in situ soil moisture data into operational distributed hydrologic models: effects of uncertainties in the data and initial model soil moisture states[J]. Advances in Water Resources, 2011,34(12):1 597-1 615.
[10] Shi Y, Davis K J, Zhang F, et al. Parameter estimation of a physically based land surface hydrologic model using the ensemble Kalman filter: a synthetic experiment[J]. Water Resources Research, 2014,50(1):706-724.
[11] Shi Y, Davis K J, Zhang F, et al. Parameter estimation of a physically-based land surface hydrologic model using an ensemble Kalman filter: a multivariate real-data experiment[J]. Advances in Water Resources, 2015,83:421-427.
[12] Neitsch S, Arnold J, Kiniry J, et al. SWAT 2009 theoretical documentation[R]∥ Texas Water Resources Institute Technical Report, 2011:406.
[13] 王晓朋, 乔 飞, 雷 坤, 等.SWAT模型在我国的研究和应用进展[J]. 中国农村水利水电,2015,(5):109-113.
[14] 王中根, 刘昌明, 黄友波. SWAT 模型的原理, 结构及应用研究[J]. 地理科学进展, 2011,22(1):79-86.
[15] Evensen G. The ensemble Kalman filter: theoretical formulation and practical implementation[J]. Ocean Dynamics, 2003,53(4):343-367.
