基于Riccati方程和LMI算法的H∞控制器的设计与实现

刘文秀，郭 伟

(1.韶关学院 物理与机电工程学院，广东 韶关 512000；2.广东松山职业技术学院，广东 韶关 512000)

基于Riccati方程和LMI算法的H∞控制器的设计与实现

刘文秀1，郭 伟2

(1.韶关学院 物理与机电工程学院，广东 韶关 512000；2.广东松山职业技术学院，广东 韶关 512000)

H∞控制是一种重要的鲁棒控制方法，它以H∞范数作为控制性能指标，是一种最优控制方法，目的是求出系统内部稳定的控制器，使闭环传递函数的无穷范数极小，达到控制的目的；以固高公司的直线一级倒立摆为控制对象，实现基于Riccati方程和LMI算法的H∞控制器设计，采用M文件及simulink实现系统建模、控制器的设计，完成系统算法的验证；实验表明，控制器的输出、倒立摆系统的状态变量变化平稳，系统具有较强的鲁棒性，系统表现出良好的动态品质，验证了H∞控制器的有效性。

倒立摆；控制器；鲁棒控制；状态反馈

0 引言

直线一级倒立摆及其载体的运动模型是一个复杂的典型多变量、非线性不稳定系统，它能反映控制过程中很多关键的问题，大多数控制理论的成果验证都是以倒立摆为研究对象。且由此产生的控制理论控制方法在工业加工领域、机器人技术、航空技术等方面都有现实的指导意义。以直线一级倒立摆为研究对象，采用一种重要的鲁棒控制方法——H∞控制方法[1]，利用Riccati方程和线性矩阵不等式LMI算法,分别设计出使系统内部稳定的控制器，达到闭环传递函数T(s)的无穷范数极小，实验证明控制器设计合理，在实际应用中是可行有效的。

1 问题描述

对于图1中的系统数学模型为:

(1)

图1 一般控制系统结构图

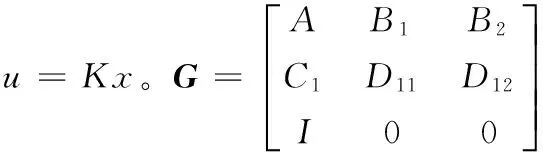
控制系统的设计要求[2]为：

1)x=0是闭环系统的局部渐进稳定平衡点，即对于任意初始状态x(0)⊂R4,x(t)→0。

(2)

式中，qi≥0(i=1,2,3,4)和ρ>0为加权系数，令:

(3)

则式(2)等价于:

(4)

定义TW(s)为W到z的闭环传递函数，表达式为：

(5)

则闭环系统的扰动抑制性能等价于:

(6)

2 H∞状态反馈控制器的设计

方法一：基于Riccati方程的H∞控制器设计[3]

针对表达式(1)的系统，当Riccati方程:

(7)

最后，美国政府在执行制裁政策时会采取个案审查原则，综合考虑个案特殊情况，再做出是否予以制裁的决定。例如，海外资产控制办公室规定了专门的特殊许可制度，对那些本应受到制裁的行为，如果通过海外资产控制办公室的个案审查并得到许可，就可以免受制裁。

方法二：基于线性矩阵不等式LMI的H∞控制器的设计[4]

(8)

成立,则系统的状态反馈控制器为:

(9)

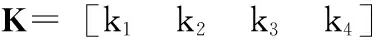
3 控制算法验证

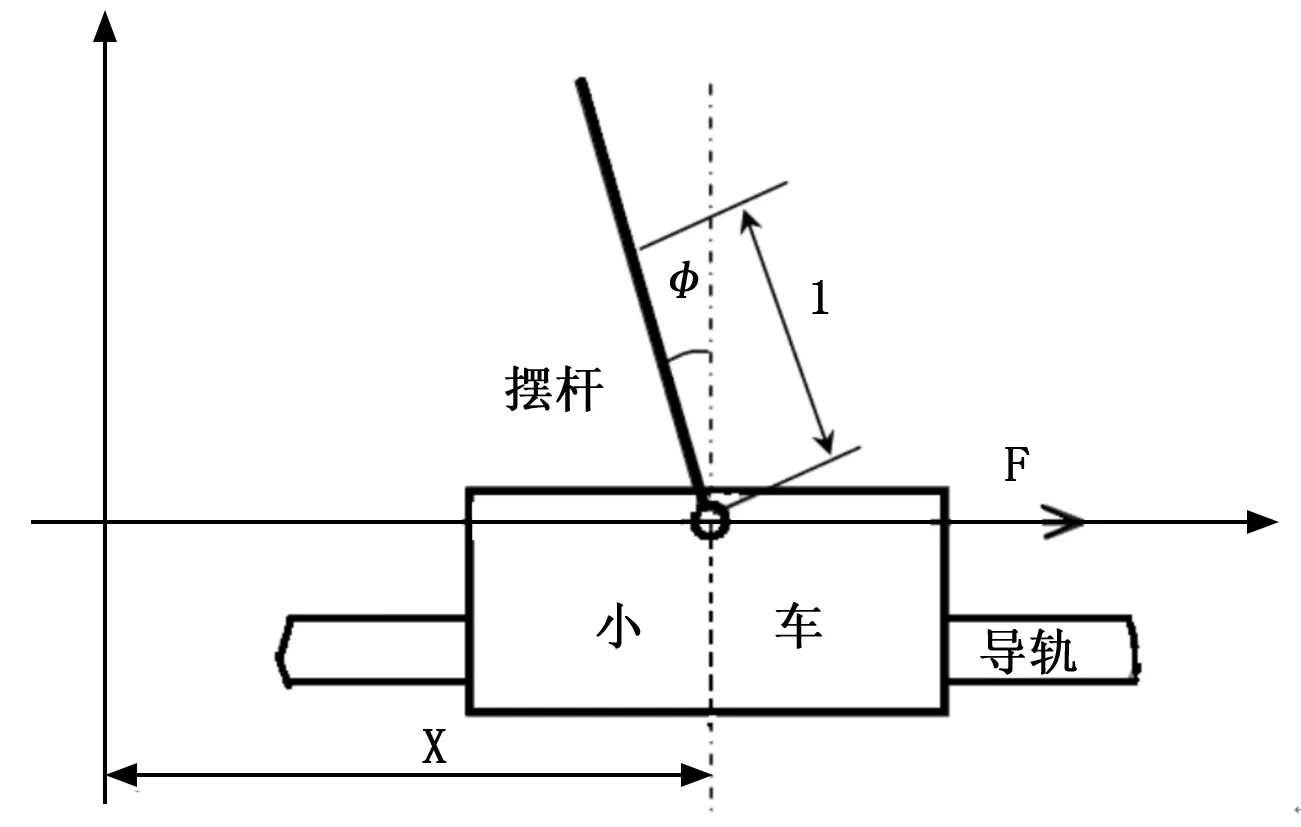
图2 直线一级倒立摆模型

系统以直线一级倒立摆为对象,验证控制算法。倒立摆系统参数来自固高公司生产的教学产品，相关参数[5]为：M代表小车质量，大小为1.096 千克；m代表摆杆质量，大小为0.109千克；b代表小车摩擦系数，大小为0 .1N/m/sec；l代表摆杆转动轴心到杆质心的长度，大小为0.25m；I代表摆杆惯量，大小为0.0034kg*m*m；F代表水平方向加在小车上的力；x是输出量小车的位置；φ是输出量摆杆与垂直方向的夹角；T是采样频率，大小为0.005秒。

对倒立摆系统进行受力分析，线性化处理，得到系统数学模型的代数方程为：

(10)

写成状态空间表达式的形式为：

(11)

把系统参数代入表达式(11)，得到以外界作用力作为系统输入的状态方程为：

(12)

B1=[0；0；0.01；0.01], B2=[0；0；0.883 167；2.356 55]。

表达式(3)中取q1=1,q2=1,q3=1,q4=1,ρ=1。

3.1 基于Riccati方程的H∞控制器的验证

第一步：利用Matlab文件编写程序计算出状态反馈增益K。

将Riccati方程转化为:

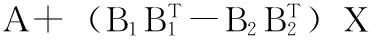
第二步：利用simulink建立系统仿真模型。

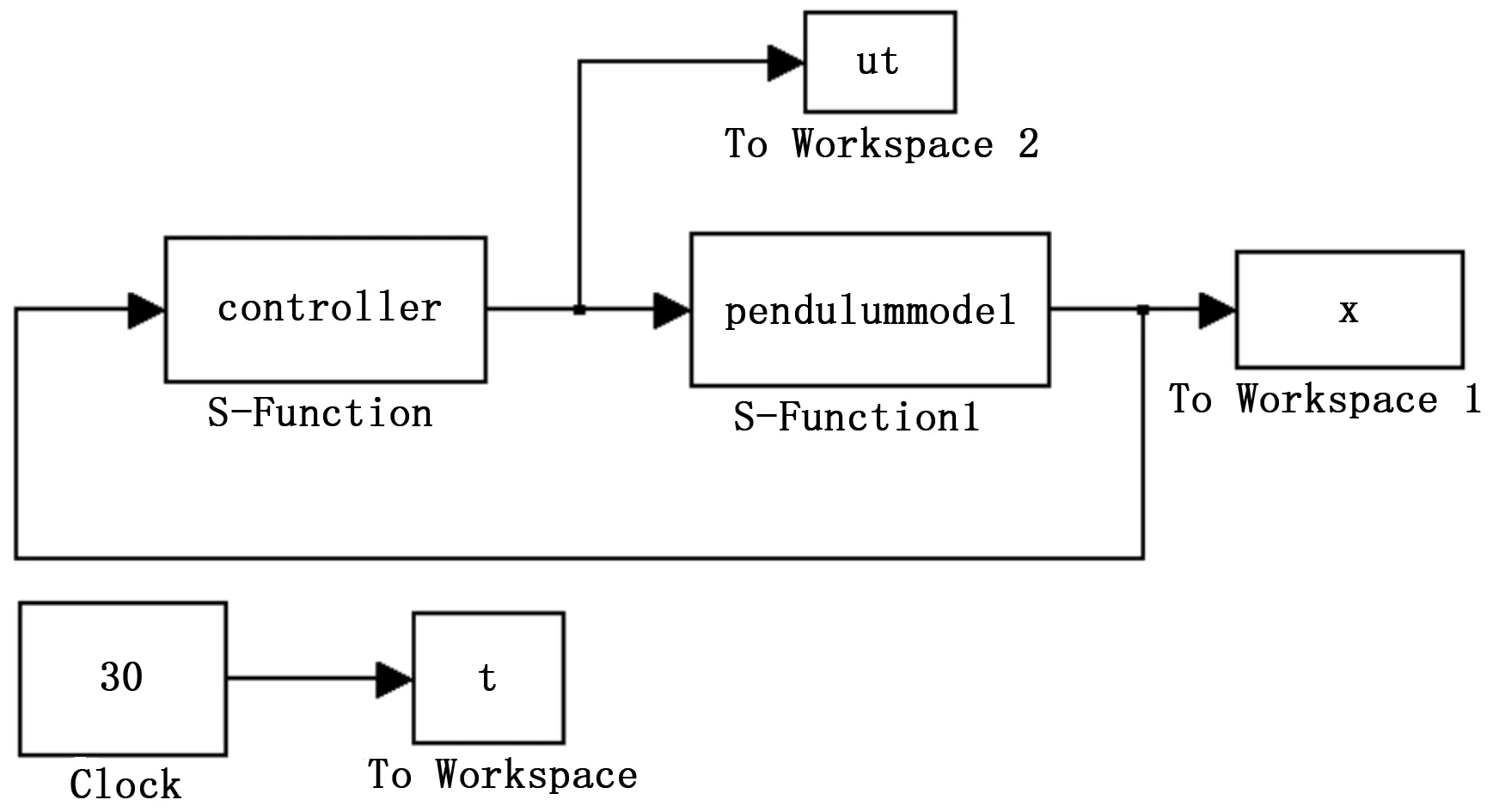
图3 系统仿真模型

利用S函数建立控制器和倒立摆模型，并在simulink下建立仿真模型如图3所示，实验数据通过绘图指令可以得到系统响应曲线，如图4、图5所示。

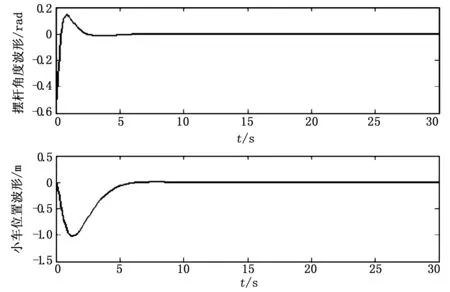
图4 基于Riccati方程的H∞控制器下系统响应波形

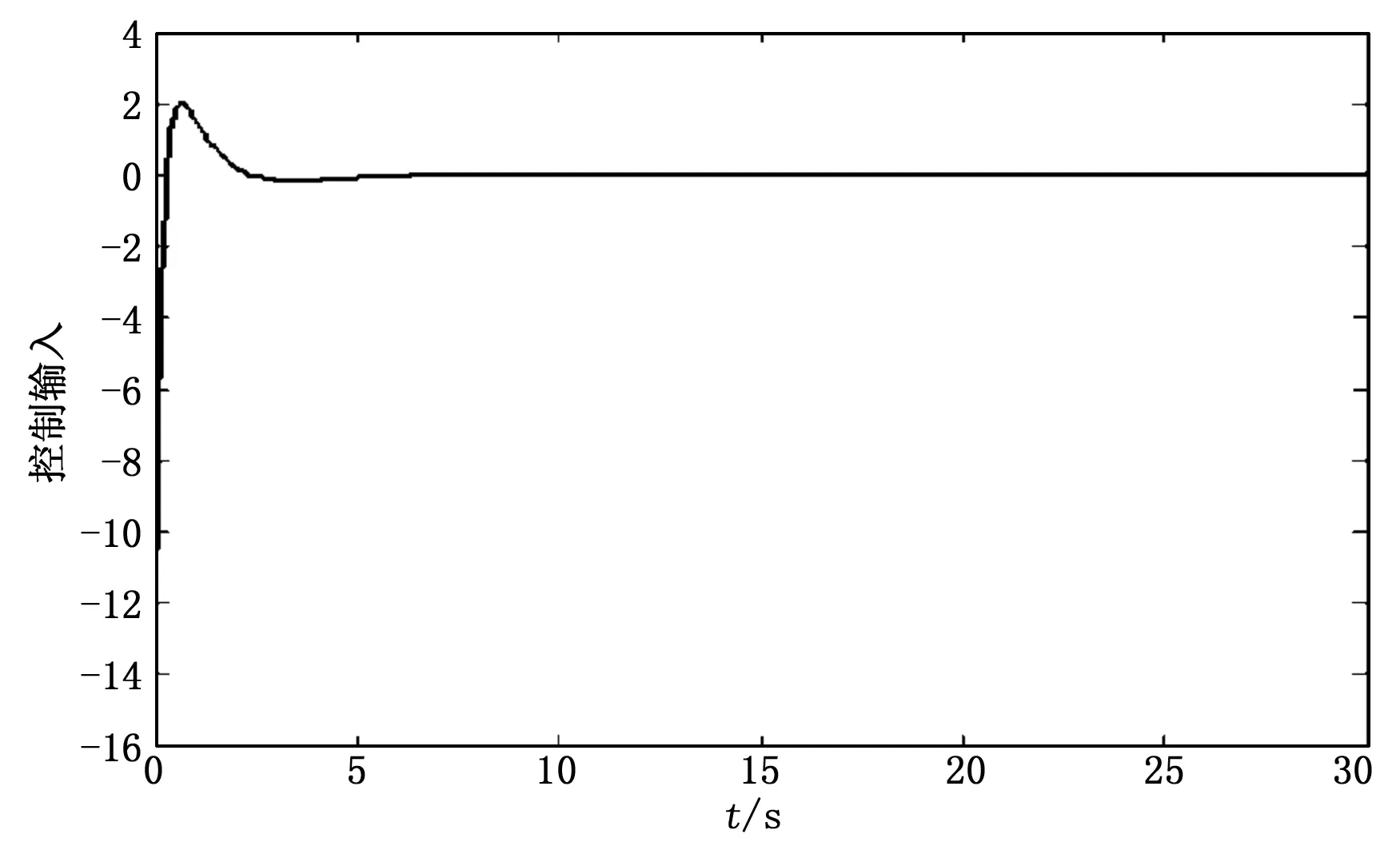
图5 基于Riccati方程的H∞控制器下控制输入波形

3.2 基于LMI的H∞控制器的验证

LMI工具箱中3个线性矩阵不等式求解函数，其中feasp解决可行性问题的求解函数。在具体实现时，首先利用setlmis和getlmis函数确定线性矩阵不等式；利用lmivar描述出现在线性矩阵不等式中的矩阵变量；利用lmiterm描述每个线性不等式中的各项内容；利用feasp函数实现不等式的求解；利用dec2mat将求解的结果按矩阵和向量的形式给出。对于直线一级倒立摆经过Matlab编程，最后求出反馈增益矩阵为K=[-4.4142 -23.9698 -17.0090 -3.2006]，在此增益矩阵下，系统响应和控制输入波形如图6、图7所示。

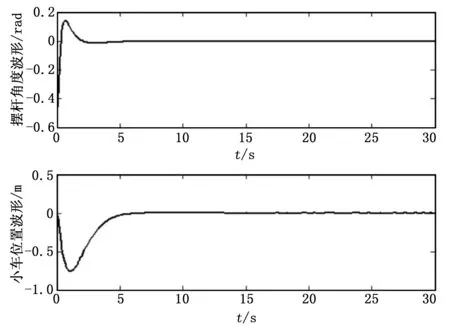
图6 基于LMI的H∞控制器的系统响应波形

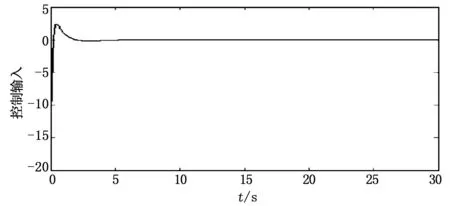
图7 基于LMI的H∞控制器的控制输入波形

4 结语

采用Riccati方程和LMI算法设计的H∞控制器对于直线一级倒立摆进行控制[6]，给出两种控制器的设计过程及方法。两种控制方法都是以系统稳定为前提，设计出反馈控制器。理论上证明该方法可行，并且通过仿真验证，说明设计的H∞控制器是可行的。

[1] 张 谦,高容翔,王海泉,等.基于人工蜂群优化的环形二级倒立摆H∞鲁棒控制器设计[J].计算机测量与控制，2015，23(8).

[2] 刘金琨.先进PID控制MATLAB仿真[M].北京：电子工业出版社，2010.

[3] 申铁龙.H∞控制理论及应用[M].北京：清华大学出版社，1996.

[4] 俞 立.鲁棒控制——线性矩阵不等式处理方法[M].北京：清华大学出版社，2002.

[5] 赵 迪, 常晓恒. T-S模糊系统量化H_∞滤波器设计[J]. 电子设计工程, 2015，21(16):112-115.

[6] 周曙光,李克俭,蔡启仲,等.基于FPGA的PLC位信息输出控制器设计[J].计算机测量与控制,2014,22(6)：145-165.

Design and Realization of H∞Controllers Based on Riccati Equation and LMI Algorithm

Liu Wenxiu1,Guo Wei2

(1.School of Physics and Mechanical and Electrical Engineering, Shaoguan University, Shaoguan 512000,China;2.Guangdong Songshan Polytechnic College, Shaoguan 512000, China)

H-infinity control is an important kind of robust control method, it with h-infinity norm as the control performance index, is a kind of optimal control method, purpose is to find the internal stability of controller, the infinite norm of the closed-loop transfer function, achieve the goal of control.With fixed high linear level inverted pendulum as control object, realize the Riccati equation and LMI algorithm based h-infinity controller design, the system is realized by using M documents and Simulink modeling, controller design, validation of the complete system algorithm, the experimental results show that the output of the controller, the change of the state variables of inverted pendulum system was stable, the system has strong robustness, the system shows good dynamic quality and effectiveness of h-infinity controller is verified.

inverted pendulum; controller ; robust control; state feedback

2016-08-25；

2016-09-21。

刘文秀(1980-)，女，内蒙古通辽人，硕士，讲师，主要从事从事自动控制方向的教学及研究。

1671-4598(2017)02-0074-03DOI：10.16526/j.cnki.11-4762/tp

TP

A