用覆盖问题解决变电站选址的探究

2017-03-21程安祺

课程教育研究·学法教法研究 2017年1期

关键词：覆盖

程安祺

【摘要】随着我国城市配电网改造的快速发展，变电站的重要性同样不可忽略，寻求变电站布置最佳方案有重要的意义。变电站的位置对电力系统的网络结构有决定性作用，起到承上启下的作用，关系到电网的经济性与稳定性。不合理的站点选址不仅可能会造成某些地方出现覆盖盲区或容量不足的情况，还会增加网络建设的成本。变电站选址时需要考虑的因素非常复杂，需要综合地理环境、物质资源、经济协助、人力资源、信号覆盖等多方面问题，本文将变电站选址问题抽象为数学模型，经过综合考虑后，将地理环境（如：楼房阻碍、海拔落差、温度、湿度等）忽略，将物质资源、经济协助与人力资源统一为经济成本，信号覆盖方面考虑是否全部覆盖及浪费的面积，忽略信号的衰弱及额定功率，构建成本函数，对成本进行最优化设计。

【关键词】变电站选址最小覆盖圆点集覆盖圆内四边形覆盖凸包

【中图分类号】TM63 【文献标识码】A 【文章编号】2095-3089（2017）01-0243-03

本文主要工作如下：

1.将变电站选址问题抽象为平面区域的圆覆盖问题；

2.对比平面区域圆覆盖与平面点集圆覆盖，通过点集覆盖寻求较优解；

3.对一些简单情况，比如点集个数n=3，4，5，覆盖圆个数m=1，2等，利用成本函数判断不同类型下变电站位置及覆盖半径；

4.分析并使用一些数学结论，比如：若一个圆能够覆盖一个区域内的所有点，则一定能够覆盖这些点构成的凸包；用几何方法求出单位圆内最大四边形为圆内接四边形。寻求平面点集最小圆覆盖方法。

在城市电网规划中，變电站选址直接影响到未来电力系统的网络结构、供电质量和运行经重要。针对信号是否能够全面覆盖以及浪费面积的计算，构建成本函数，从而得到最佳的选址方案。

1.构建铺设成本和功率模型

变电站铺设时，需要考虑铺设成本与功率两个方面。若忽略铺设成本而只考虑最小化功率，则只需在每个负荷点附近铺设一个变电站即可，显然，这种方案是不现实的。因此，不难看出变电站的铺设成本与功率相制约。

设C为总成本，c为每个变电站的成本，m为变电站的个数，s为浪费的面积（变电站总覆盖面积减去需要覆盖的面积，包括重复覆盖面积及无用覆盖面积），s0为待覆盖区域的面积，r为每个变电站覆盖区域的半径，为每个变电站的材料成本（与r2成正比），c2为每个变电站的人员工资、运输费用等（与r成正比），k1为浪费面积与成本之间的比例系数，k2为变电站半径与材料成本的之间的比例系数，k3为变电站半径与人员工资、运输费用等之间的比例系数。

计算时不妨令k1=k2=k3=1，最后成本函数为：

2.将区域覆盖问题转化为平面点集覆盖问题

由于平面区域的最小圆覆盖问题是NP问题。因此，我们不可能给出令人满意的结果。考虑到在实际应用中，变电站覆盖也不需要区域某个地区全部的点，只需要覆盖某些小区、写字楼等集中用电区。所以我们将区域覆盖问题转化为平面点集的覆盖，将集中用电区抽象为平面上的点。

本文考虑某个地区范围内需要供电的n个负荷点U={u1，u2，…un}，用最小圆区覆盖这n个点。本文从简单情况做起，考虑m=1，2，即用一个或两个圆覆盖区域上的n个点。

2.1 假定m=1

此时s0等于0，易知，r越小，总成本C越小

a）n=1，只需将变电站放在这个点A处即可；

b）n=2，变电站应放在A、B两点中点处，覆盖区域半径为AB/2；

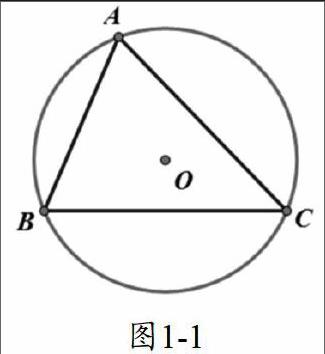
c）n=3，文献3中已经给出详细证明，这里本文使用几何画板软件给出图像，证明过程不再重复。当△ABC为锐角三角形时，通过几何画板可得最小覆盖圆是它的外接圆；变电站应放在△ABC的外心O处，覆盖区域半径为OA，如图1-1。

图1-1

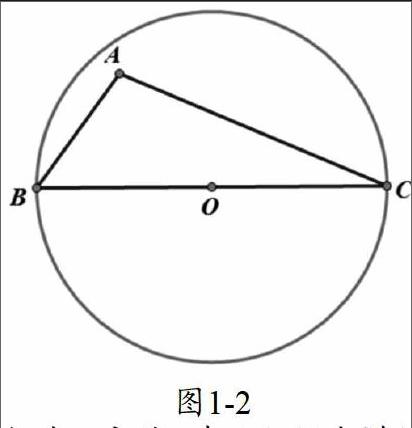
当△ABC为钝角三角形时，通过几何画板可得其最小覆盖圆为钝角所对边为直径的圆。不妨设AB边。为最长边，变电站应放在A、B两点中点处，覆盖区域半径为AB/2，如图1-2

图1-2

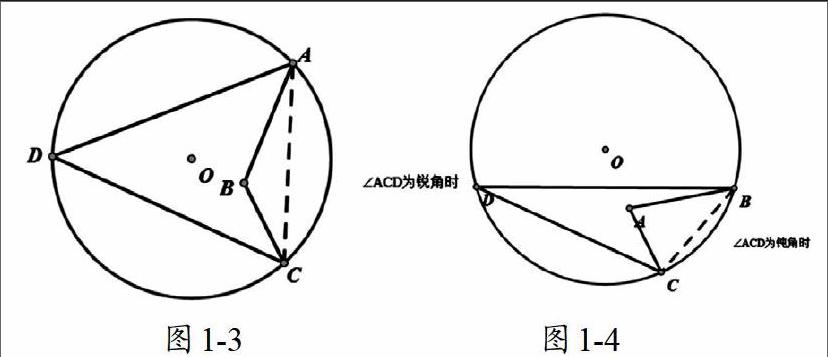
d）n=4，类似地，文献3中已经给出详细证明，这里本文使用几何画板软件给出图像，证明过程不再重复。当四边形ABCD为凹四边形时，不妨设∠ABC>180°，此时△ACD的最小覆盖圆即为四边形ABCD的最小覆盖圆，变电站应放在△ABC的外心O处，覆盖区域半径为OA，通过几何画板比较容易得到，如图1-3，1-4

当四边形ABCD为凸四边形时不妨设∠D+∠B≥∠A+ ∠C且∠B≥∠D，此时△ACD的最小覆盖圆为四边形ABCD的最小覆盖圆。

2.2 假定m=2

a）引理：若一个圆O能够覆盖区域S内的所有点，则圆O一定能覆盖S的凸包。

证明：

取S凸包上的定点为A1，A2，……，An，……，不妨设OA1为OAn中最大的一项，OA2为次大的一项，取A1A2所在直线为l，过O作l的垂线交l于BOB≤max{OA1，OA2}，因此B在圆O内，因此凸包内的所有点均在圆O内，如图2-1，2-2

通过这个结论我们可以看到，限定条件为只使用一个圆覆盖时，平面区域覆盖与平面点集覆盖有某种统一性。这也说明本文考虑点集覆盖问题的合理性。

b）m=2，n=5（这五个点A，B，C，D，E构成凸五边形，且顺时针排列）当∠A，∠B，∠C，∠D，∠E均为钝角时，取一点，使得该点与两个不相邻两点的距离之和最小，不妨设该点为A，则变电站1应放在AC中点O1处，覆盖区域半径为O1A，变电站2应放在AD中点O2处，覆盖区域半径为O2A，如图2-3-1，2-3-2，2-3-3

证明：因为∠ABC为钝角，所以B在以AC为直径的圆O1内，所以△ABC在圆O1内，同理，E在以AD为直径的圆O2内，所以△ADE在圆O2内。若∠ACD为钝角，则C在圆O2内，则△ACD在圆O2内，同理；若∠ADC为钝角，则D在圆O1内，则△ACD在圆O1内；若∠ACD与∠ADC均为锐角，则过A作CD的垂线交于F，△ACF在圆O1中，△ADF在圆O2中，此时△ACD包含在圆O1与圆O2中。因此圆O1和圆O2能够覆盖五边形ABCDE。

当有且仅有∠A为锐角时，取一点（C或D），使得该点与两个不相邻定点的距离之和最小，分别连接该点与不相邻两点，取中点分别为O1，O2，其余同上，如图2-4-1，2-4-2

证明：

因为∠CBA为钝角，所以点B在圆O1内，因此△ABC在圆O1内，同理，△CDE在圆O2内。若∠CEA为钝角，则点E在圆O1内，因此△CAE在圆O1内；若∠CAE，∠CEA均为锐角，则过C作线段AE的垂线，设垂足为F，易知△CAF在圆O1内，△CEF在圆O2内。

当有且仅有∠A，∠C为锐角时，连接AC，然后选取AD与CE中较短的线段，不妨设AD

证明：

因为∠ABD为钝角，所以点B圆O1内，因此△ABC在圆O1内，同理，△ADE在圓O2内。若∠ADC为钝角时，点D在圆O1内，因此△ADC在圆O1内；若∠ADC为锐角时，过A作线段CD的垂线，设垂足为F，易知，△ACF在圆O1内，△ADF在圆O2内。

2.3 回到区域覆盖问题

既然一般的区域覆盖问题是NP问题，本文逆向思考这个问题。将至转化为给定一系列圆的位置，求它可以覆盖的区域的面积的最大值。这里为方便起见，区域去成凸多边形。

（1）当m=1时，如何在半径为1的圆O内放置一个四边形ABCD，使其面积最大？

解：

1.若A，B，C，D四个点不都在圆O上，则可将该点与半径的连线平移到圆O上，必会使四边形ABCD面积变大，如图3-1，此后A，D均指代在圆上的对应点

2.连接AC，将四边形ABCD划分为△ABC和△ACD，它们均以AC为底边，要想使面积更大，应增大两个三角形的高。过O作AC垂线交圆于B`，D`，连接AB`，CB`，AD`，CD`，如图3-2