抽象的数学知识须运用直观教学方式
2017-03-21王广阔
王广阔
抽象是从众多的事物中抽取出共同的、本质性的特征,而舍弃其非本质的特征。直观是通过对客观事物的直接接触而获得的感性认识。二者处在认知活动的不同层次,甚至是对立的。在小学阶段,学生的思维处在具象向抽象过渡的阶段,数学教学如果停留在直观的层面,就没有达成目标,而一味地抽象,学生又难以理解。以直观的方式揭示抽象的结论是教学浅出而深入的重要方式。
一、抽象的结论:在直观操作中领悟
不完全归纳法在小学数学教学中经常运用,然而仅仅从少数的几个例子中得出一个抽象的结论显然不符合数学严谨的特点。但是,运用演绎法和完全归纳法又不太适用小学阶段的学生。有没有兼顾二者的做法呢?答案是肯定的。江苏省优质课竞赛上,Y老师的一个教学环节给了我们很好的启示。
教师出示一个钉子板并在上面围成了一个底6高4的直角三角形。
教师先让学生口算出这个三角形的面积,接着拉动三角形的顶点不断向右移动,将三角形变成其他几个底6高4的三角形,并让学生计算这些三角形的面积。学生开始时一个一个算,算着算着,就不计算了,直接报出答案。教师故作诧异地问道:“你们怎么都算得这么快?”学生不约而同的说道:“这些三角形的面积都相等,都是12平方厘米。”教师接着问:“这些三角形有什么关系?”学生回答:“它们都是等底等高的三角形。”教师进一步追问:“这样的三角形有多少个?它们的面积都相等吗?”学生思考后回答道:“等底等高的三角形有无数个,它们的面积都相等。”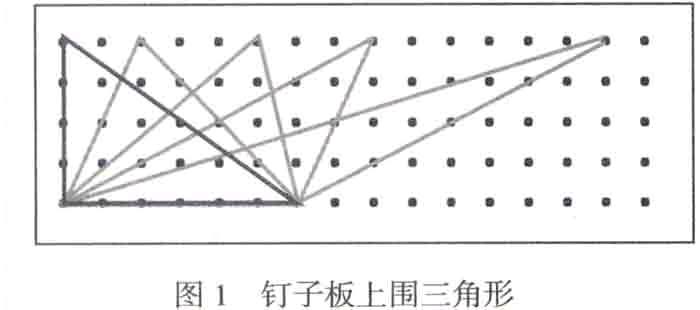
普普通通的钉子板,教师充分利用“移动顶点”的方式帮助学生领悟了“等底等高的三角形,面积相等”的道理。教学方式直观形象,师生交流生动有趣,学习效果深入有效。
二、抽象的道理:在动态演示中理解
Y老师的教学过程生动形象,借助直观的操作激发了学生的想象,帮助学生归纳了“等底等高的三角形,面积相等”这一抽象的结论。教学至此,已经十分出色,但笔者认为仍然可以更进一步:在动态演示中揭示抽象的道理。
笔者教学时,也像Y老师一样借助钉子板总结出了结论。接着又用多媒体出示了一个直角三角形(用一条一条长短不同的线段搭成的三角形)。接着借助多媒体演示这些长短不一的线段向右平移不同的距离,并定格为形状不同但等底等高的三角形(图2)。
引导学生说一说:“这些三角形的面积相等吗?为什么?”学生在交流后得出一致的认识:“这些三角形都是由无数条相同的线段搭成的,只是搭的方法不同,每个图形还包含着同样的线段,面积大小不变。”
Y老师的教学更多地采用的是归纳法来揭示“等底等高的三角形,面积相等”这一结论。笔者的设计则是选择另一条路径,从面积的本质意义上来揭示“等底等高的三角形,面积相等”这一结论,渗透了微积分的思想。两种教学路径都需要充分发挥学生的想象力,借助有限的直观演示,激发了学生无限的空间想象,以想象为纽带连接直观和抽象之间的空白。
三、抽象的思路:在直观的想象中获得
想象是一种特殊的思维形式,是人在头脑里对已储存的表象进行加工改造形成新形象的心理過程。在理解知识获得结论的过程中想象发挥着重要的作用,在运用知识解决实际问题的过程中,想象同样发挥重要的作用。
一块底30米,高12米的平行四边形的菜地,中间铺了一条2米宽的小路(图3)。你能求出菜地的面积吗?
学生采用了两种不同的方法。方法一:用平行四边形的面积减去中间小路的面积。方法二:想象着把两边的不规则图形通过平移转化成一个平行四边形。在求中间小路的面积时,学生要思考这条不规则小路的面积该怎样计算。有些同学想象着把这条不规则小路看作是一条条长度相等的线段拼成的图形(图3(2)),进一步平移可以转化成一个底2高12的平行四边形(图3(3))。
从上述案例可以看出,在解决实际问题的过程中,学生能否解决,一方面需要学生具有扎实的“双基”,另一方面则需要学生具有良好的想象力。在观察眼前事物的时候,能够借助想象的力量,对头脑中的表象进行加工、创造,改造出新的形象,从而巧妙转化原先的问题,获得解决问题的策略和方法。培养学生解决问题的能力,我们不能一味地运用逻辑演绎的方法帮助学生理解解决问题的思路,而要有意识地去发展学生想象、类比等直觉思维的能力。
小学阶段,我们需要直观的教,但是直观的教并不是将学生的认识固定在直观认识的层面,而要让学生理解抽象的结论和道理,但是抽象的结论和道理并不一定要进行抽象的演绎。在直观和抽象之间,还有想象、直觉等这些中间地带。抽象的结论,可以在直观操作中领悟;抽象的道理,可以在动态演示中理解;抽象的思路,可以在直观的想象中获得。
[责任编辑:陈国庆]
