基于协整的期货跨品种套利研究
——以黑色产业链为例
2017-03-20周亮
周 亮
(湖南财政经济学院,湖南长沙410205)
一、引 言
2016年是“十三五”的开局之年,钢铁业推进供给侧结构性改革,粗钢产量增速得到控制,全年全国粗钢产量80837万吨,增长1.2%;生铁产量70074万吨,增长0.7%;钢材产量113801万吨,增长2.3%。我国大中型钢企主要采取长流程进行钢材生产,即以铁矿石、焦炭为主要原料实现高炉炼铁、转炉炼钢。正常是1.6-1.7吨铁矿出1吨钢,同时需要消耗0.3吨-0.5吨焦炭。横向比较来看,铁矿石约占原料成本的40%,焦炭约占20%,废钢约占10%。纵向比较来看,近年来,随着铁矿石年度协议价逐步转向月度定价甚至现货定价,定价周期的缩短使得其价格波动全面体现在钢材成本上,铁矿石的成本占比由低价时的30%左右上升至高价时的50%以上。因此,铁矿石和焦炭的价格波动一直对钢厂和贸易商等产业链企业的利润有重大影响。2016年10月、11月、12月焦煤焦炭上演“绝世双焦”,短短几个月时间,双焦的价格便实现了翻倍,而铁矿石价格继2016年自低点大幅反弹之后,2017年初继续开启了波澜壮阔的涨幅。原材料价格的大幅上涨侵蚀着钢厂的利润,可喜的是成材价格也大幅上涨,但是价格的暴涨暴跌对于现货厂商来说始终是不利的,因此随着焦炭、铁矿石及螺纹钢期货运行的不断成熟,现货企业通过期货市场实现套期保值的需求越来越强烈,而专业投资机构也可以通过期货进行单边投机或跨品种套利参与到黑色产业链中来。
跨品种套利主要是指在买入或卖出某种商品(合约)的同时,卖出或买入相关的另一种商品(合约),当两者的差价收缩或扩大至一定程度时,平仓了结的交易方式。虽然此方法具有一定可行性,但是跨品种套利作为外联套利,其价差或比值通常是沿着趋势变化的,其一旦出现历史比值的高点(或价差)为今年比值的低点时,会造成套利的巨大损失。但是总体来说,套利的风险比起单边投机而言要小很多,尤其对于有产业背景的现货商而言,对跨品种套利进行深入研究,亦是规避原材料及成品价格波动的重要手段。
二、文献综述
国内外学着对期货套利进行了大量的研究。从研究对象来看,主要集中在农产品期货、原油期货及股指期货之间的套利研究。Tzang和Leuthold(1990)对大豆、豆粕和豆油之间的套利进行了研究,发现在这三者之间进行套期保值交易可以有效降低风险和持有成本[1]。Rechner和Poitras(1993)模拟大豆压榨的过程,以压榨利润作为判别标准,通过设置合理的阈值来进行套利,可以取得不错的收益[2]。Berhanu和 Paulson(1999)对原油、汽油和取暖油期货进行套利研究,认为投资者可以通过三者之间不合理的价格关系进行套利[3]。Haigh和Holt(2002)用不同方法对原油及其衍生品期货进行套利研究,发现MGARCH 方法在交易获利中最优[4]。 Dunis et al(2006,2008)运用非线性协整与多种神经网络方法对WTI原油和无铅汽油进行套利研究,较好地实现了套利交易[5][6]。 国内学者如刘建和等(2016)运用协整检验、误差修正模型研究了大豆、豆粕、豆油三者价格之间长期存在的相互关系,发现我国大豆期货及豆粕和豆油期货三者进行跨商品套利可行,能够获得正向的套利收益率,在不同的开平仓阀值下,Elman神经网络模型较均值回归模型能够得到更好的套利结果[7]。李宇霆(2016)则通过GARCH模型研究了沪深300股指期货与上证50股指期货的跨品种套利[8]。孔令涛(2015)以风格动量效应为视角,在以日度数据频率下,根据游程检验的方法,发现A股市场存在显著的大小盘风格动量效应,并基于此,使用中证500股指期货和上证50股指期货进行跨品种套利,发现在有限的风险之下可以获得非常可观的累计收益[9]。李世伟(2011)利用沪深300股指期货的实际交易数据,借助对现有的协整理论进行改进的套利方法建立模型,实施跨期套利,结果发现,改进的协整策略可以取得较好的套利效果[10]。邢亚丹等(2015)采用标准差距离法基于沪深300股指期货数据,构造了1分钟高频跨期套利策略,在考虑交易成本的情况下,该策略年化收益为 138.84%[11]。
在具体的套利方法上,学者们采取的均为均值回归方法,即通过协整、误差修正模型、GARCH等时序分析方法来研究商品期货之间长期存在的相互关系,从而设计相应的套利策略。Wahab et al(1994)运用协整、误差修正模型等方法研究了黄金和白银两者价格之间的关系,利用移动平均法实现两者之间的跨品种套利[12]。Simon(1999)运用GRACH和协整检验方法对大豆压榨价差进行了研究,发现存在长期均衡即短期偏差最终会回归均衡[13]。Liu和chou(2003)运用误差修正模型对黄金和白银进行研究,认为可以根据两者间的风险溢价实现套利机会[14]。 Mitchell(2007)运用协整、均值回归等方法,发现大豆、豆粕和豆油三者之间的压榨价差短期偏离长期均衡状态后并不一定会以震荡的方式进行均值回归[15]。国内学者如靳朝翔等(2016)通过设置不同的开平仓阀值,运用BP神经网络模型和NAR动态神经网络模型在样本区间内进行套利策略对比研究,结果发现NAR动态神经网络模型的预测能力更强,其套利策略在螺纹钢、铁矿石和焦炭三者间进行跨品种套利效果更好[16]。覃良文等(2015)利用Engle-Granger检验法,检验上海沪铜期货两个近月合约收盘价数据的长期均衡关系,并利用HP滤波法将两序列分别分解为长期趋势和短期波动周期性两种成分,实证结果表明,基于HP滤波的套利方法,平滑指数越小,套利利润越高,与传统未进行HP滤波的套利方法相比,套利成功率较高,风险能得到有效控制,且投资者有较高的收益[17]。朱丽蓉等(2015)对期货市场上的统计套利进行实证研究,提出了协整模型、误差修正模型和基于协整关系的GARCH3个统计套利模型,结果表明,基于协整关系的GARCH模型是三个统计套利模型中最优的[18]。
综上所述,目前的研究主要集中在用均值回归方法对跨期或者跨商品期货的统计套利。研究农产品、原油及股指期货的较多,对黑色产业链进行研究的较少,研究两种商品或跨期商品的套利较多,研究多产品套利的较少;同时,研究方法上主要集中在长期关系确定方法的选择和比较,对阈值的设定一般没做深入探讨。因此,笔者拟采用协整方法对黑色产业链,主要包括螺纹钢、铁矿石及焦炭三者的期货产品进行统计研究,并采用期望函数对开仓阈值的设定进行一定探讨。
三、套利模型的选择
1.数据选取及来源
由于我国铁矿石期货2013年10月才上市,因此笔者选择2014年1月1日-2016年11月12日的所有日线数据,以收盘价为准。由于铁矿石、螺纹钢及焦炭每年1、5、10月合约持仓量和成交量均最大,因此选择每年1、5、10月份的合约为主力合约。对所有合约进行移仓换月,在每个合约交割月的前一个月的第一天换到下一个主力合约,即每年4月1日开始持有10月份合约、9月1日开始持有下一年1月份合约、12月1日开始持有下一年5月份合约,从而形成连续交易数据。总共获得697组日收盘价数据,以2014年和2015年共489组数据为样本内的数据,主要用来确定协整关系
所有数据均来自东方财富金融数据库,数据处理均使用EXCEL以及EVIEWS6.0软件。
2.描述性统计及相关性分析
螺纹钢、铁矿石及焦炭三组数据的描述性统计如表1所示。由表1可以看出,螺纹钢的均值为2474.5,最大值和最小值分别为3590、1616,标准差为494.5;铁矿石的均值为502.3,最大值和最小值分别为907、284,标准差为157.7;焦炭的均值为1003.5,最大值和最小值分别为2153、606.5,标准差为235.8。可以看出,三个品种的价格均波动剧烈。

表1 数据描述性统计
对三组数据进行相关性分析,所得结果如表2所示。可以看出,螺纹钢与铁矿石的价格相关性很高,达到了0.96;螺纹钢与焦炭的相关性也有0.77。

表2 相关性分析结果
3.平稳性及协整关系检验
在对变量做协整检验之前,首先需要对变量进行平稳性检验,原序列及差分序列的ADF检验值如表3所示。可以看出,螺纹钢、铁矿石及焦炭的原序列均是一阶平稳序列,因此可以做协整检验。

表3 变量的平稳性检验
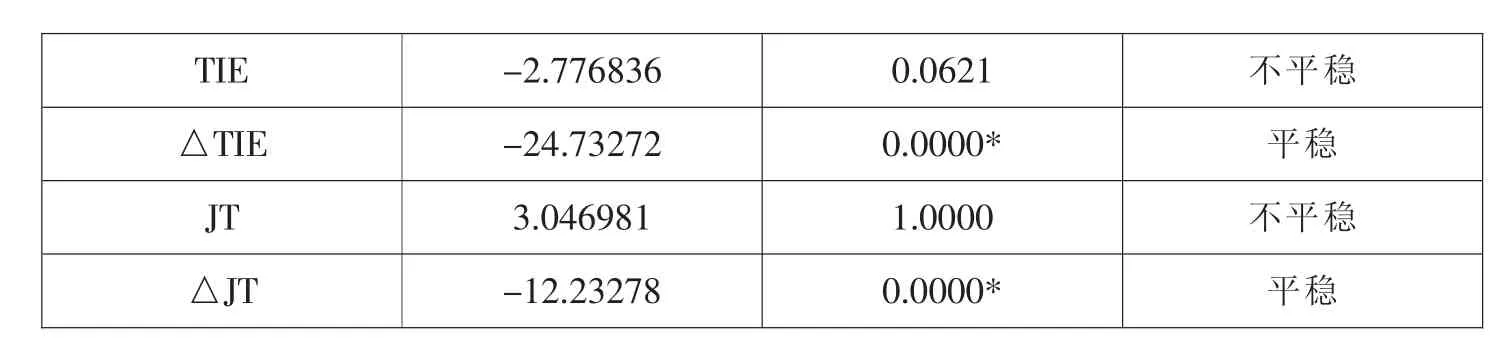
注:★表示在5%的水平下显著。
分别对“螺纹钢-铁矿石”、“螺纹钢-焦炭”以及“螺纹钢-铁矿石-焦炭”的协整关系做检验,结果如表4所示。可以看出,螺纹钢与铁矿石、螺纹钢与焦炭以及三者之间均存在协整关系。
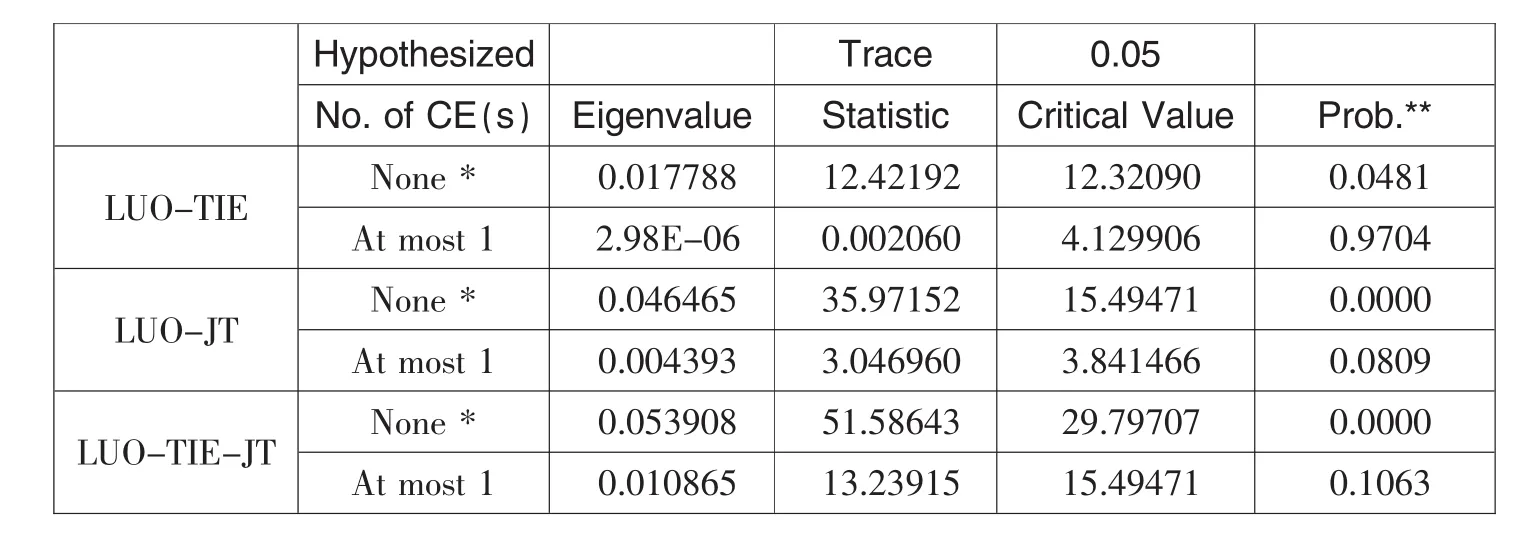
表4 协整关系检验结果
4.协整模型确定
螺纹钢与铁矿石、螺纹钢与焦炭以及三者之间的协整模型如表5所示。可以看出,模型II的调整R2只有0.59,进一步验证了焦炭与螺纹钢的相关关系不强。但是由模型III可以看到,用铁矿石和焦炭一起对螺纹钢进行回归,得到了很好的效果,调整R2达到了0.95,比单纯用铁矿石预测的0.92更好。

表5 协整模型
由于期货市场只能取手数的整数倍,因此设置模型I的套利比率为1:3,套利模型为:DIR1=LUO-3*TIE;模型II的套利比率为1:1.6,套利模型为DIR2=LUO-1.6*JT;模型III的套利比率为1:2.5:0.5,套利模型为DIR3=LUO-2.5*TIE-0.5*JT。三者的统计图如图1-图3所示:

图1 DIR1统计图及时序图

图2 DIR2统计图及时序图
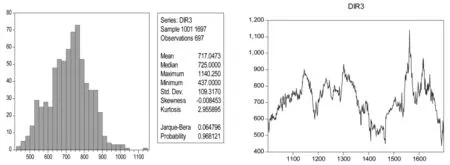
图3 DIR3统计图及时序图
由图1-图3可以看到,根据Jarque-Bera统计量来看,在10%的显著性水平下,只有DIR3符合正态分布,DIR1和DIR2均不符合正态分布;时序图上也可以看到,DIR1回归特征不明显,DIR2波动毫无规则,DIR3相对来说具有均值回复特性。由于统计套利主要是利用样本的均值回归,因此正态分布的样本更符合要求。因此,只适合对螺纹钢、铁矿石及焦炭三者之间的协整关系进行套利。
四、套利方案及检验
1.套利方案设计
由前面的长期协整检验可知,螺纹钢、铁矿石及焦炭三者之间存在长期协整关系,其差值DIR3符合均值为717、标准差为109的正态分布。虽然短期来看,价差可能偏离均值,但是长期看,价差会回复到均值。同时为了规避风险,笔者增加了延后开仓及提前平仓两个策略。延后开仓指的是,等价差突破阈值后,反向回归穿越阈值时再建仓。提前平仓指的是,实际交易中经常会发现价差虽然在向均值回归的方向回归,但没有回归到均值,而是在离均值一定距离外又掉头远离均值,因此在均值以前进行平仓。
因此,具体开平仓规则为:当|DIR3-717|〉a*109并再次向下跌破a*109时,进行套利开仓操作;当|DIR3-717|〈b*109时,如果此时持有套利头寸,则进行平仓操作;为了防止协整关系因为不可控因素而破坏,设置2.58倍标准差(意味着价差超过止损界限的概率只有1%)为止损线,即如果持有套利头寸,当头寸在同方向超过2.58*109时执行止损平仓。
2.开平仓阈值的确定
如果a取值过小,可能导致频繁交易,昂贵的交易成本会侵蚀大量的利润甚至导致亏损;如果a取值过大,则可能会错过很多本可以盈利的机会,导致交易次数过少,降低总的套利利润。
设统计套利效益的期望函数为:E(α*σ)=β*R(α*σ)*φ-1(α*σ),其中 β 为常数,R(α*σ)为阈值取 a 时的套利利润空间,φ-1(α*σ)为可以实施套利交易的概率。笔者对a取0取到2.5并以0.1为步长分别来计算可套利概率、利润空间及效益期望函数,结果如图4-图6所示。
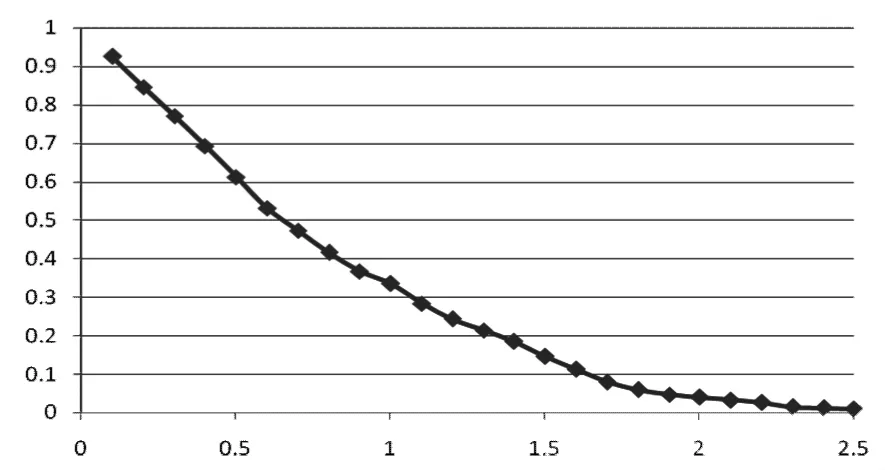
图4 价差序列超过阈值a的概率
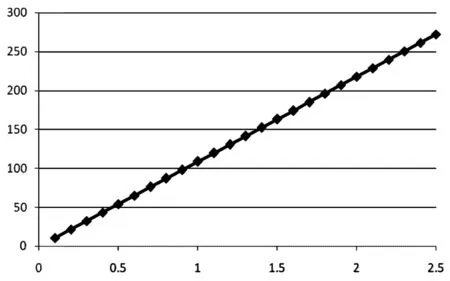
图5 阈值取a时的可套利利润空间

图6 阈值取a时的套利期望收益
由图6可以看出,当a=1时,套利交易的期望收益率取得最大值,因此笔者对开仓阈值的取值为1。
对于平仓阈值,笔者根据其他研究,定为0.05。
3.交易保证金及手续费
交易所对螺纹钢、铁矿石、焦炭的最低保证金要求分别为8%、8%和15%,但是实际券商要求的保证金一般为12%、12%和20%,笔者采用券商要求的保证金比例来进行测算。
券商普遍对螺纹钢、铁矿石及焦炭收取手续费的标准单边分别为成交金额的4%%、4.8%%、4.8%%,按照11月份相对高价(螺纹钢3000、铁矿石600、焦炭2000,远高于平均价格)估计,按照螺纹钢:铁矿石:焦炭=1:2.5:0.5的比例,进行一次完整的套利操作预计需要手续费为5.5元/吨。
4.套利交易结果
根据以上交易原则,分别在样本内和样本外进行测验,所得结果如表6所示。可以看出,在样本内总共进行了7次套利,样本外进行了2次套利,均取得了正收益。值得注意的是,在2016年4月,价差最高偏差达到了423,远远超过了止损线2.58*109=281,但是由于采取了延后开仓策略,因此在之前并没有持仓,有效的避免了一次亏损。从收益率上来看,样本内获得了32.18%的年化收益率、样本外获得了26.62%的年化收益率,均较为不错。
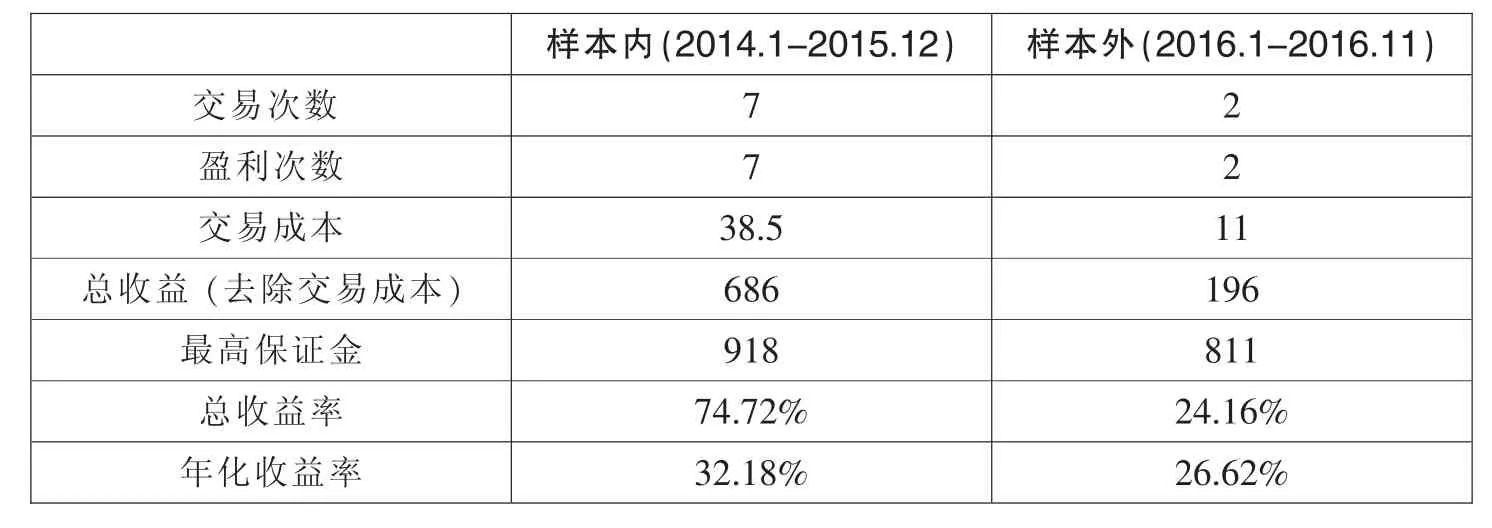
表6 套利交易结果
五、结 语
笔者选取2014年1月1日-2016年11月12日的铁矿石、螺纹钢及焦炭期货的所有主力合约数据,首先通过协整检验发现,螺纹钢与铁矿石两者之间,及螺纹钢、铁矿石与焦炭三者之间的协整效果较好;再根据Jarque-Bera统计量分析发现,螺纹钢、铁矿石及焦炭三者之间的协整关系进行套利最优;再通过阈值测算,发现开仓阈值为1时,套利交易的期望收益率最大。对样本内外的数据进行套利测试,发现样本内获得了32.18%的年化收益率、样本外获得了26.62%的年化收益率,均较为不错。
由实证结果可以看出,套利交易实现了较为不错的收益。但是在研究方法上还有很大拓展空间:首先,笔者采用的协整方法属于均值回归策略,但是已经有大量的文献均是采用神经网络对价差进行预测,从而实现套利;其次,笔者采用的数据为日数据,虽然在做检验时数据样本充足,但是相对小时线数据或更加高频的数据来说,无疑丢失了更多信息以及可套利交易的样本;最后,笔者只是将样本简单分为样本内和样本外,但是期货品种之间的协整关系并不是简单固定的,因此在采用更大样本数据的前提下,可以对协整模型进行滚动求解,从而使得品种之间的比率关系采用了更近的数据,从而使得套利交易更加有效。
[1] Tzang D.N,Leuthold R.M.Hedge Ratios under Inherent Risk Reduction in a Eommodity Complex[J].Journal of Futures Markets,1990,(5):497-504.
[2] Rechner D,Poitras G.Putting on the Crush:Day Trading the Soybean Complex Spread[J].The Journal of Futures Markets,1993,(1):61-75.
[3] Berhanu G.P,Paulson S.A.Seasonality in Petroleum Futures Spreads[J].The Journal of Futures Markets,1999,(18):581-598.
[4] Haigh M.S, HoltM.T.Crack Spread Hedging:Accounting for Timevarying Volatility Spillovers in the Energy Futures Markets[J].Journal of Applied Econometrics,2002,(3):269-289.
[5] Dunis C.L,Laws J,Evans B.Modelling and Trading the Gasoline Crack Spread:A Non-linear Story[J].Derivatives Use Trading&Regulation,2006,(1):126-145.
[6] Dunis C.L,Laws J,Evans B.Trading Futures Spread Porfolios:Applications of Higher Order and Recurrent Networks[J].The European Journal of Finance,2008,(6):503-521.
[7]刘建和等.大豆期货合约均值回归套利策略和Elman神经网络套利策略对比研究[J].湖南财政经济学院学报,2016,(3):13-20.
[8] 李宇霆.基于 GARCH 模型的股指期货套利策略研究[N].期货日报,2016-08-15(03).
[9] 孔令涛.基于风格动量效应的股指期货套利策略[J].金融理论与实践,2015,(10):77-80.
[10]李世伟.基于协整理论的沪深300股指期货跨期套利研究[J].中国计量学院学报,2011,(2):198-202.
[11]邢亚丹等.跨期套利收益与风险来源探究——基于沪深300股指期货高频跨期套利策略[J].投资研究,2015,(10):98-109.
[12] Wahab M, Cohn R,LashgariM.The Gold-silverSpread:Integration,Cointegration,Predictability and Exante Arbitrage[J].Journal of Futures Markets, 1994,(6):709-756.
[13] Simon D.P.The Soybean Crush Spread:Empirical Evidence and Trading Strategies[J].Journal of Futures Markets,1999,(3):271-289.
[14] Liu S.M, Chou C.H.Parities and Spread Trading in Gold and Silver Markets:A Fractional Cointegration Analysis[J].Applied Financial Economics,2003,(12):879-891.
[15] Mitchell J.B.Soybean Crush Spread Arbitrage:Trading Strategies and Market Efficiency[J].Journal of Risk&Financial Management,2007,(1):63-96.
[16]靳朝翔等.基于神经网络模型的商品期货跨品种套利策略[J].云南财经大学学报(社科版),2016,(4):150-160.
[17] 覃良文等.基于 HP滤波和协整理论的期货套利研究[J].湖北大学学报(自科版),2015,(6):570-576.
[18] 朱丽蓉等.基于我国期货市场的统计套利研究[J].数理统计与管理,2015,(4):730-740.
